Algebraic K-theory
-
General Introduction
See also Abstract K-theory and much more.
See also Motivic cohomology
See also Motivic homotopy theory
<]]> -
Search results
<]]> -
Online References
Weibel's book project
Lectures notes of Schlichting
Weibel's K-theory handbook chapter: K0691
Short course by Levine
Gillet: K-theory and Intersection theory. Treats relation to Chow groups, coniveau filtration, Gersten's conjecture and more. Also the stable homotopy-theoretic viewpoint on algebraic K-theory, and K-theory as sheaf hypercohomology, and other basic things. Extremely nice article!
A survey by Arlettaz: Algebraic K-theory of rings from a topological viewpoint
Garkusha on a general construction recovering Karoubi-Villamayor and Quillen K-theory for rings.
The Development of algebraic K-theory before 1980, by Charles A. Weibel: K0343
Opérations sur la K-théorie algébrique et régulateurs via la théorie homotopique des schémas, by Joël Riou
Some notes by Rosenberg on relations with topology and analysis.
Something on the plus constuction by Berrick
Weibel: The development of algebraic K-theory before 1980
Brown and Gersten: Algebraic K-theory as generalized sheaf cohomology (1973)
For
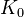 and
and 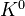 of a variety, see de Jong's notes on Algebraic de Rham cohomology
of a variety, see de Jong's notes on Algebraic de Rham cohomologyThomason's ICM talk 1990: The local to global principle in algebraic K-theory.
<]]> -
Paper References
See Kuku in Handbook of algebra Vol 4, for a survey of a number of different types of algebraic K-th including Volodin K-th.
Bass: Algebraic K-theory (1968) in K-th folder. Treats K0 and K1 or rings. Background on rings and projective modules. Reciprocity laws (ch VI and XIII). Finiteness thms for rings of arithmetic type (Ch X).
Read Quillen\'s original paper!! Here is a review/summary. See also the sequel by Grayson. There is also a survey article by Swan which seems to summarize much of Quillen\'s paper, possibly taking into account later developments.
Geisser in the K-theory handbook is excellent.
Grayson has a survey in the Motives volumes.
Thomason-Trobaugh: Higher algebraic K-theory of schemes and of derived categories. In the Grothendieck Festschrift, Vol III.
Milnor: Intorduction to algebraic K-theory (1971)
Rosenberg: Algebraic K-theory and its applications.
Soulé et al: Lectures on Arakelov Geometry: First chapter treats Chow groups, with product induced from isomorphism with K-groups. Good quick review of algebraic K-theory.
Many papers by Gillet, including stuff on Chern classes in a very general setting.
Grayson Hangzhou lectures in K-th folder: Brief intro to algebraic K-theory, very readable, with end remarks on motivic cohomology.
Handbook of K-th?
Friedlander's ICTP lectures in K-th folder: Very nice introduction to algebraic K-theory.
Levine Morelia lecture notes: Basic intro to algebraic K-theory of rings and schemes.
Manin: Lectures on the K-functor in algebraic geometry. In K-th folder. Among other things, he covers monoidal transformations and Riemann-Roch.
Milnor: Introduction to algebraic K-th (in K-th folder). Covers mainly K2, note that these notes came before Quillen's work.
Rosenberg in K-th folder: Basic intro to algebraic K-theory of rings: concrete approaches to K0, K1, K2, negative K-theory, plus and Q constructions, cyclic homology.
Srinivas: Algebraic K-th book, K-th folder. Comprehensive introduction to algebraic K-theory of rings and schemes. Advanced topics include the Merkurjev-Suslin thm and localization for singular varieties.
Weibel: The K-book. Looks like a very good introduction to algebraic K-theory. See his webpage for the latest version, I have a version from Sep 2011.
<]]> -
Definition
First define K-groups of an exact cat. Then the cat of locally free sheaves of finte rank give K-groups, and if
 is noetherian, the cat of coherent sheaves gives G-groups. If
is noetherian, the cat of coherent sheaves gives G-groups. If  is regular, the two kinds of groups coincide.
is regular, the two kinds of groups coincide.From the definition, K-groups are contravariant functors from schemes to abelian groups. G-groups are contravariant for flat maps only.
For K-theory of rings, one brief introduction is Burgos-Gil, chapter 9. Using the Cartan-Serre theorem, can obtain information about the K-groups of
 by studying the homology of
by studying the homology of 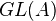 ("the homology of an H-space is a Hopf algebra").
("the homology of an H-space is a Hopf algebra").The 5 papers by Neeman on K-theory of triangulated categories: K0507, K0508, K0509, K0510, K0511. Perhaps the K-theory handbook is a better source for this material.
On Voevodsky's algebraic K-theory spectrum BGL, by Ivan Panin, Konstantin Pimenov, and Oliver Roendigs: Under a certain normalization assumption we prove that the Voevodsky's spectrum BGL which represents algebraic K-theory is unique over the integers. Following an idea of Voevodsky, we equip the spectrum BGL with the structure of a commutative ring spectrum in the motivic stable homotopy category. Furthermore, we prove that under a certain normalization assumption this ring structure is unique over the integers. We pull this structure back to get a distinguished monoidal structure on BGL for an arbitrary Noetherian base scheme. K0838
http://mathoverflow.net/questions/1006/motivation-interpretation-for-quillens-q-construction
<]]> -
Properties
Charles A. Weibel, Homotopy algebraic $K$-theory (pp. 461--488) (1987, some proceedings)
http://mathoverflow.net/questions/984/algebraic-k-theory-and-tensor-products
arXiv:1301.3815 Universality of K-Theory fra arXiv Front: math.AG av José Luis González, Kalle Karu We prove that graded K-theory is universal among oriented Borel-Moore homology theories with a multiplicative periodic formal group law.
<]]> -
Standard theorems
See this review for different views on the localisation sequence
<]]> -
Open Problems
<]]> -
Connections to Number Theory
Kolster: K-theory and arithmetic (K-th folder). Notes on zeta values of rings of integers, algebraic K-groups, etale cohomology, Iwasawa theory, motivic cohomology, Vandiver's conjecture.
Interesting paper by Dwyer and Mitchell.
See all papers by Morrow for higher local fields and arithmetic surfaces. For example: arXiv:1211.1533 K-theory of one-dimensional rings via pro-excision fra arXiv Front: math.KT av Matthew Morrow This paper studies "pro-excision" for the K-theory of one-dimensional (usually semi-local) rings and its various applications. In particular, we prove Geller's conjecture for equal characteristic rings over a perfect field of finite characteristic, give the first results towards Geller's conjecture in mixed characteristic, and we establish various finiteness results for the K-groups of singularities (covering both orders in number fields and singular curves over finite fields).
http://mathoverflow.net/questions/10204/any-reason-why-k23z-has-order-65520
For K-theory of (rings of integers of) global fields, see Weibel's survey in the Handbook of K-theory. Here is something about nontorsion elements. Here is something about even K-groups of Q and relations to cyclotomic conjectures, by Banaszak and Gajda
arXiv:1002.2936 Splitting in the K-theory localization sequence of number fields from arXiv Front: math.KT by Luca Caputo Let p be a rational prime and let F be a number field. Then, for each i>0, there is a short exact localization sequence for K{2i}(F). If p is odd or F is nonexceptional, we find necessary and sufficient conditions for this exact sequence to split: these conditions involve coinvariants of twisted p-parts of the p-class groups of certain subfields of the fields F(\mu{p^n}) for n\in N. We also compare our conditions with the weaker condition WK^{et}_{2i}(F)=0 and give some example.
MR1760901 (2001i:11082) Bloch, Spencer J.(1-CHI) Higher regulators, algebraic $K$-theory, and zeta functions of elliptic curves.
arXiv:0910.4005 The extended Bloch group and algebraic K-theory from arXiv Front: math.KT by Christian K. Zickert We define an extended Bloch group for an arbitrary field F, and show that this group is canonically isomorphic to K3^ind(F) if F is a number field. This gives an explicit description of K3^ind(F) in terms of generators and relations. We give a concrete formula for the regulator, and derive concrete symbol expressions generating the torsion. As an application, we show that a hyperbolic 3-manifold with finite volume and invariant trace field k has a fundamental class in K_3^ind(k) tensor Z[1/2].
arXiv:1101.5477 On special elements in higher algebraic K-theory and the Lichtenbaum-Gross Conjecture from arXiv Front: math.KT by David Burns, Herbert Gangl, Rob de Jeu We conjecture the existence of special elements in odd degree higher algebraic K-groups of number fields that are related in a precise way to the values at strictly negative integers of the derivatives of Artin L-functions of finite dimensional complex representations. We prove this conjecture in certain important cases and also provide other evidence (both theoretical and numerical) in its support.
arXiv:1208.2137 Wild Kernels and divisibility in K-groups of global fields from arXiv Front: math.NT by Grzegorz Banaszak In this paper we study the divisibility and the wild kernels in algebraic K-theory of global fields $F.$ We extend the notion of the wild kernel to all K-groups of global fields and prove that Quillen-Lichtenbaum conjecture for $F$ is equivalent to the equality of wild kernels with corresponding groups of divisible elements in K-groups of $F.$ We show that there exist generalized Moore exact sequences for even K-groups of global fields. Without appealing to the Quillen-Lichtenbaum conjecture we show that the group of divisible elements is isomorphic to the corresponding group of \' etale divisible elements and we apply this result for the proof of the $lim^1$ analogue of Quillen-Lichtenbaum conjecture. We also apply this isomorphism to investigate: the imbedding obstructions in homology of $GL,$ the splitting obstructions for the Quillen localization sequence, the order of the group of divisible elements via special values of $\zeta_{F}(s).$ Using the motivic cohomology results due to Bloch, Friedlander, Levine, Lichtenbaum, Morel, Rost, Suslin, Voevodsky and Weibel, which established the Quillen-Lichtenbaum conjecture, we conclude that wild kernels are equal to corresponding groups of divisible elements.
<]]> -
Computations and Examples
[arXiv:1207.2225] K-theory of toric varieties revisited fra arXiv Front: math.AT av Joseph Gubeladze After surveying higher K-theory of toric varieties, we present Totaro's old (c. 1997) unpublished results on expressing the corresponding homotopy theory via singular cohomology. It is a higher analog of the rational Chern character isomorphism for general toric varieties. Apart from its independent interest, in retrospect, Totaro's observations motivated some (old) and complement other (very recent) results. We also offer a conjecture on the nil-groups of affine monoid, extending the nilpotence property. The conjecture holds true for K_0.
See Rognes for a computation in which he mentions K-theory as an infinite loop space.
Geisser and Levine: The K-theory of fields in characteristic p (Invent. Math., 2000)
Oriented Cohomology and Motivic Decompositions of Relative Cellular Spaces , by Alexander Nenashev and Kirill Zainoulline
For the K-theory of finite fields, see Jardine.
For tori and toric varieties, see Panin and Merkurjev
Something on henselization of local ring: K113
Higher K-theory of complex surfaces: K0328
K-Theory of non-linear projective toric varieties, by Thomas Huettemann: K0752
Panin: On a theorem of Hurewicz and K-theory of complete DVRs.
Daniel R. Grayson, On the $K$-theory of fields (pp. 31--55) (1987, some proceedings)
Panin, I. A. Algebraic $K$-theory of Grassmannian manifolds and their twisted forms. (Russian) Funktsional. Anal. i Prilozhen. 23 (1989), no. 2, 71--72, translation in Funct. Anal. Appl. 23 (1989), no. 2, 143--144.
See many articles by Hesselholt, Angeltveit, Gerhardt, also more recent than the Kth handbook.
Articles by Weibel et al using cdh techniques?
arXiv:1006.3413 Algebraic K-theory of the first Morava K-theory from arXiv Front: math.KT by Christian Ausoni, John Rognes We compute the algebraic K-theory modulo p and v_1 of the S-algebra ell/p = k(1), using topological cyclic homology.
arXiv:1101.1866 On the algebraic K-theory of Z/p^n from arXiv Front: math.KT by Vigleik Angeltveit We study the algebraic K-theory groups of the ring Z/p^n using the cyclotomic trace map to the topological cyclic homology spectrum TC(Z/p^n). We prove that Kq(Z/p^n) is finite for all n \geq 2 and q \geq 1 and that the order satisfies |K{2i-1}(Z/p^n)|/|K{2i-2}(Z/p^n)|=p^{(n-1)i}(p^i-1)$ for all i \geq 2. We also determine the group Kq(Z/p^n) for all n \geq 2 and q \leq 2p-2.
We approach TC(Z/p^n) by filtering Z/p^n by powers of p and studying several spectral sequences related to this filtration.<]]> -
History and Applications
<]]> -
Some Research Articles
arXiv:0907.2710 Algebraic K-theory, A^1-homotopy and Riemann-Roch theorems from arXiv Front: math.AG by Joël Riou. In this article, we show that the combination of the constructions done in SGA 6 and the A^1-homotopy theory naturally leads to results on higher algebraic K-theory. This applies to the operations on algebraic K-theory, Chern characters and Riemann-Roch theorems.
Gabber: K-theory of Henselian local rings and Henselian pairs (1992)
Thomason: Bott stability in algebraic K-theory (1986)
Panin: The Hurewicz theorem and K-theory of complete discrete valuation rings (1986)
Landsburg: Some filtrations on higher K-theory and related invariants (1992)
Knudson on the K-theory of elliptic curves
Kahn on reciprocity laws
On the K-theory of local fields, by Lars Hesselholt and Ib Madsen
Detecting K-theory by cyclic homology, by Wolfgang Lueck and Holger Reich K0753
k-invariants for K-theory of curves over global fields, by Dominique Arlettaz and Grzegorz Banaszak: K0770
Berrick and Casacuberta on a universal space for the plus construction. See also K0314
The Farrell-Jones isomorphism conjecture for finite co-volume hyperbolic actions and the algebraic K-theory of Bianchi groups, by Ethan Berkove, F. Thomas Farrell, Daniel Juan-Pineda, and Kimberly Pearson: K0288
Hughes and Prassidis "We formulate and proove a geometric version of the Fundamental Theorem of Algebraic K-Theory which relates the K-theory of the Laurent polynomial extension of a ring to the K-theory of the ring."
Weibel and Pedrini: Higher K-theory of complex varieties, and The higher K-theory of Real Curves: K0429
Two-primary algebraic K-theory of pointed spaces, by John Rognes: K0236
Algebraic K-theory of topological K-theory, by Christian Ausoni and John Rognes: K0405
Huettemann: Algebraic K-Theory of Non-Linear Projective Spaces
On the K-theory of complete regular local F_p-algebras, by Thomas Geisser and Lars Hesselholt: K0435
Some remarks concerning mod-n K-theory, by Eric M. Friedlander and Mark E. Walker: K0451
On the K-theory of stable generalized operator algebras, by Hvedri Inassaridze and Tamaz Kandelaki: K0497
K-theory of semi-local rings with finite coefficients and étale cohomology, by Bruno Kahn
Anderson, Karoubi, Wagoner: Relations between higher algebraic K-theories. (1973). In LNM 341.
Weibel: A Quillen-type spectral sequence for the K-theory of varieties with isolated singularities (1988). Abstract: We construct a spectral sequence to compute the algebraic K-theory of any quasiprojective scheme X, when X has isolated singularities, using an explicit flasque resolution of the K-theory sheaves. This is a generalization of Quillen's construction for nonsingular varieties. The explicit resolution makes it possible to relate K-theory to intersection theory on singular schemes. Key words: Quasi-projective scheme - spectral sequence - sheaves - homotopy Cartesian cubes
Suslin: On the K-theory of local fields.
Bass: Algebraic K-theory
Suslin and Wodzicki: Excision in algebraic K-theory (1992)
J. F. Jardine, The homotopical foundations of algebraic $K$-theory (pp.\ 57--82) (1987)
Bloch: The Postnikov tower in algebraic K-theory
arXiv:1009.3235 On the Algebraic K-theory of Monoids from arXiv Front: math.KT by Chenghao Chu, Jack Morava Let $A$ be a not necessarily commutative monoid with zero such that projective $A$-acts are free. This paper shows that the algebraic K-groups of $A$ can be defined using the +-construction and the Q-construction. It is shown that these two constructions give the same K-groups. As an immediate application, the homotopy invariance of algebraic K-theory of certain affine $\mathbb{F}1$-schemes is obtained. From the computation of $K2(A),$ where $A$ is the monoid associated to a finitely generated abelian group, the universal central extension of certain groups are constructed.
<]]> -
Other Information
Henri Gillet - University of Illinois, Chicago Title: K-Correspondences and complexes of Motives Abstract: I shall discuss how to use algebraic K-theory to construct an enrichment of the category of varieties over the category of chain complexes of rational vector spaces, and how to use this to define maps between the homological weight complexes of singular varieties (such as pull back with respect to morphisms of finite tor-dimension). (Joint work with C. Soulé)
"K-th is not an invariant of the triangulated cat, but it is an invariant of the infty-one cat. See example by Schlichting I think, and observation of Toen-Vezzosi."
http://mathoverflow.net/questions/11404/what-is-an-euler-system-and-the-motivation-for-it
http://mathoverflow.net/questions/39499/when-is-the-k-theory-presheaf-a-sheaf
From http://www.maths.soton.ac.uk/pure/researchabstract.phtml?keyword=K-theory
The higher algebraic K-theory of geometric objects such as algebraic varieties or, more generally, schemes over Noetherian rings, was contructed by Quillen (circa 1970). Almost immediately exciting applications of algebraic K-theory we found in algebraic geometry by Bloch, who showed how to recover the Chow groups of a variety from its algebraic K-theory sheaf. Generalised to a form called the Bloch-Ogus-Gabber Theorem, the discovery of Quillen and Bloch has become
motivic complexes'' which would, for algebraic varieties in characteristic zero, unify algebraic K-groups, Chow groups, singular cohomology, de Rham cohomology as well as the cohomology theories constructed for schemes by Grothendieck and his school in the 1960's. The existence of various categories ofUnrecognised command "\'"one of the fundamental results of modern algebraic geometry''. For example, the connection between algebraic K-theory and Chow groups led Soul\'{e} and Beilinson to make a number of very refined, precise conjectures about the existence of higher Chow groups'' - sometimes known as ``motivic cohomology''. Then Suslin and Voevodsky used the Bloch-Lichtenbaum spectral sequence to calculate the K-theory of curves and surfaces over an algebraically closed field. Finally Voevodsky (c.1997) devised an entirely new construction of motivic cohomology which enabled him to determine the $2$-adic part of the K-theory of any field admitting the resolution of singularities. Voevodsky's work establishes (at the prime $p=2$) the 1973 conjecture of Quillen and Lichtenbaum, which relates K-theory with mod $p^{n}$ coefficients to Grothendieck's \'{e}tale cohomology with mod $p^{n}$ coefficients. Incidentally, Snaith and his collaborators proved the surjectivity half of the Quillen-Lichtenbaum conjecture for general smooth, projective schemes (Inventiones 1982). In arithmetic-algebraic geometry one tries to relate all these things to algebraic geometry coming from curves over number fields - for example, Wiles' work is in this area. Snaith has worked on the connections between Galois actions on motivic objects - the central one being given by K-groups - and special values of L-functions. This is an extremely active area and the maojor open questions are: the Birch-Sinnerton-Dyer conjecture, the Brumer-Stark conjecture, the Lichtenbaum conjecture, the Quillen-Lichtenbaum conjecture, the Beilinson conjectures, the Kato conjecture, the Tate conjecture, the Hodge conjecture, the Coates-Sinnott conjecture and one of mine - the Chinburg-Snaith conjecture concerning the "Wiles unit".
Snaith uses connective topological K-theory to study Chow groups in arithmetic-algebraic geometry as above and to study the famous problem of the existence/non-existence of framed manifolds of Arf-Kervaire invariant one (a problem that is the natural successor to JF Adams' "Hopf invariant one" work.
<]]>
higher Chow groups'' - sometimes known as ``motivic cohomology''. Then Suslin and Voevodsky used the Bloch-Lichtenbaum spectral sequence to calculate the K-theory of curves and surfaces over an algebraically closed field. Finally Voevodsky (c.1997) devised an entirely new construction of motivic cohomology which enabled him to determine the $2$-adic part of the K-theory of any field admitting the resolution of singularities. Voevodsky's work establishes (at the prime $p=2$) the 1973 conjecture of Quillen and Lichtenbaum, which relates K-theory with mod $p^{n}$ coefficients to Grothendieck's \'{e}tale cohomology with mod $p^{n}$ coefficients. Incidentally, Snaith and his collaborators proved the surjectivity half of the Quillen-Lichtenbaum conjecture for general smooth, projective schemes (Inventiones 1982). In arithmetic-algebraic geometry one tries to relate all these things to algebraic geometry coming from curves over number fields - for example, Wiles' work is in this area. Snaith has worked on the connections between Galois actions on motivic objects - the central one being given by K-groups - and special values of L-functions. This is an extremely active area and the maojor open questions are: the Birch-Sinnerton-Dyer conjecture, the Brumer-Stark conjecture, the Lichtenbaum conjecture, the Quillen-Lichtenbaum conjecture, the Beilinson conjectures, the Kato conjecture, the Tate conjecture, the Hodge conjecture, the Coates-Sinnott conjecture and one of mine - the Chinburg-Snaith conjecture concerning the "Wiles unit".
Snaith uses connective topological K-theory to study Chow groups in arithmetic-algebraic geometry as above and to study the famous problem of the existence/non-existence of framed manifolds of Arf-Kervaire invariant one (a problem that is the natural successor to JF Adams' "Hopf invariant one" work.
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.