Algebraic cobordism
-
General Introduction
Algebraic cobordism was defined by Levine and Morel - see the book linked to below on Levine's web page for a longer introduction and a summary of their results. It is an algebro-geometric analogue of complex cobordism theory in algebraic topology. Algebraic cobordism is the universal oriented cohomology theory on Sm/k where k is a field of characteristic zero. The theory described by Levine and Morel is a geometric construction. There is also a homotopical construction of algebraic cobordism, as the bigraded cohomology theory represented (in the sense of motivic stable homotopy theory) by the spectrum MGL. This latter theory is referred to as Motivic cobordism here. There is a comparison theorem (I think) which gives an isomorphism between algebraic cobordism (which is graded by one integer n) and the motivic cobordism groups in degrees (n, 2n).
See also Motivic homotopy theory, Motivic cobordism
See also Oriented cohomology, Orientable cohomology, Oriented homology, Oriented Borel-Moore homology
<]]> -
Search results
<]]> -
Online References
Book by Levine and Morel. There are also some other notes on Levine's web page, for example this, and also something probably redundant here and here
<]]> -
Paper References
<]]> -
Definition
There are two things called algebraic cobordism; conjecturally, they are the same. The first one is constructed by Levine as a "universal oriented cohomology theory". The other is constructed by Voevodsky, as a theory represented by a certain spectrum.
For the construction of Levine, see Oriented cohomology.
<]]> -
Properties
arXiv:1301.3292 Descent for algebraic cobordism fra arXiv Front: math.AG av José Luis González, Kalle Karu We prove the exactness of a descent sequence relating the algebraic cobordism groups of a scheme and its envelopes. Analogous sequences for Chow groups and K-theory were previously proved by Gillet.
<]]> -
Standard theorems
Levine-Morel mentions two main theorems in their first chapter, which do not follow immediately from universality of Levine's algebraic cobordism.
Thm: For
a field of char zero, the canonical HM from the Lazard ring (with a certain grading) to the coefficient ring is an isomorphism.Thm: Let
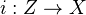be a closed immersion of smooth varieties over , with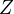 
of codimension 
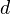in 
, and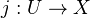 
the open immersion of the complement. Then the sequence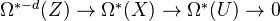
(
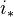followed by 
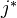) is exact.Thm: Rost's degree formula.
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
Oriented Cohomology and Motivic Decompositions of Relative Cellular Spaces , by Alexander Nenashev and Kirill Zainoulline
Algebraic cobordisms of a Pfister quadric, by Alexander Vishik and Nobuaki Yagita (Computes both kinds and show that they agree!)
It seems like Naumann's preprint with Ostvaer and Spitzweck also computes operations in algebraic cobordism.
<]]> -
History and Applications
Chow rings of excellent quadrics, by Nobuaki Yagita: K0787
<]]> -
Some Research Articles
Some remarks on Real and algebraic cobordism, by Po Hu and Igor Kriz: K0398
Something on Brown-Peterson spectra and formal group laws, by Vezzosi.
Yagita: Algebraic cobordism of simply connected Lie groups.
A blow-up relation in algebraic cobordism, by Alexander Nenashev, and something more in K0816, simplifying something by Levine and Pandharipande
A universality theorem for Voevodsky's algebraic cobordism spectrum, by Ivan Panin, Konstantin Pimenov, and Oliver Roendigs: K0846
On the relation of Voevodsky's algebraic cobordism to Quillen's K-theory, by Ivan Panin, Konstantin Pimenov, and Oliver Roendigs: K0847
Snaith: Algebraic cobordism and K-theory (1979), Memoirs of the AMS 21. Also other old papers by Snaith, such as LNM673 paper.
arXiv:0907.4437 Algebraic Cobordism of Classifying Spaces from arXiv Front: math.AG by Dinesh Deshpande We define algebraic cobordism of classifying spaces, \Omega^(BG) and G-equivariant algebraic cobordism \Omega^_G(-) for a linear algebraic group G. We prove some properties of the coniveau filtration on algebraic cobordism, denoted F^j(\Omega^(-)), which are required for the definition to work. We show that G-equivariant cobordism satisfies the localization exact sequence. We calculate \Omega^(BG) for algebraic groups over the complex numbers corresponding to classical Lie groups GL(n), SL(n), Sp(n), O(n) and SO(2n+1). We also calculate \Omega^(BG) when G is a finite abelian group. A finite non-abelian group for which we calculate \Omega^(BG) is the quaternion group of order 8. In all the above cases, we check that \Omega^(BG) is isomorphic to MU^(BG).
arXiv:1209.5793 Stable and Unstable operations in Algebraic Cobordism from arXiv Front: math.AG by Alexander Vishik We describe additive (unstable) operations from a theory A^* obtained from Algebraic Cobordism of M.Levine-F.Morel by change of coefficients to any oriented cohomology theory B^. We prove that there is 1-to-1 correspondence between the set of operations, and the set of transformations: A^n((P^{\infty})^{\times r}) ---> B^m((P^{\infty})^{\times r}) satisfying certain simple properties. This provides an effective tool of constructing such operations. As an application, we prove that (unstable) additive operations in Algebraic Cobordism are in 1-to-1 correspondence with the L\otimes_Z Q-linear combinations of Landweber-Novikov operations which take integral values on the products of projective spaces. On our way we obtain that stable operations there are exactly L-linear combinations of Landweber-Novikov operations. We also show that multiplicative operations A^ ---> B^* are in 1-to-1 correspondence with the morphisms of the respective formal group laws. We construct Integral (!) Adams Operations in Algebraic Cobordism, and all theories obtained from it by change of coefficients, giving classical Adams operations in the case of K_0. Finally, we construct Symmetric Operations for all primes p (these operations in Algebraic Cobordism, previously known only for p=2, are more subtle than the Landweber-Novikov operations, and have applications to rationality questions), as well as the T.tom Dieck - style Steenrod operations in Algebraic Cobordism.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.