Algebraic de Rham cohomology
-
General Introduction
Algebraic de Rham cohomology is a Weil cohomology.
See also de Rham cohomology
<]]> -
Search results
<]]> -
Online References
Some notes by Clark
Friedrich on periods and algebraic de Rham cohomology
<]]> -
Paper References
Hartshorne: On the de Rham cohomology of algebraic varieties.
Hartshorne: Algebraic de Rham cohomology
<]]> -
Definition
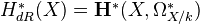(hypercohomology of the de Rham complex)<]]> -
Properties
de Rham cohomology is a Weil cohomology with coefficients
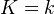on the category of smooth projective varieties over 
.Cup product comes from wedge product on the de Rham complex.
Functoriality: Given a morphism of schemes
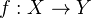, we have a map of complexes 
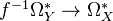, which induces a map on cohomology.Homotopy invariance: de Jong writes: Let
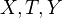be quasiprojective -varieties, and let 
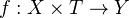, with 
smooth and connected. Then for any two -points of , the inclusion of the associated fibers induce the same map on cohomology.<]]> -
Standard theorems
An affine bundle induces isomorphism on cohomology.
Kunneth decomposition.
Trace map: Let
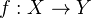be a finite morphism, with 
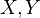of the same dimension. Then we have a map 
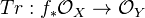. For properties, see de Jong.Poincaré duality and Tate twists, see de Jong.
Projective bundle theorem.
Let
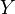be a nonsingular divisor on a smooth projective variety 
, and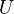 
the open complement. Then, using the logarithmic de Rham complex, one gets a long exact sequence
<]]> -
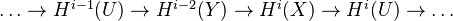Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
Easy to compute cohomology of affine and projective space (see de Jong).
<]]> -
History and Applications
<]]> -
Some Research Articles
arXiv:1207.6193 Completions and derived de Rham cohomology fra arXiv Front: math.AG av Bhargav Bhatt We show that Illusie's derived de Rham cohomology (Hodge-completed) coincides with Hartshorne's algebraic de Rham cohomology for a finite type map of noetherian schemes in characteristic 0; the case of lci morphisms was a result of Illusie. In particular, the E_1-differentials in the derived Hodge-to-de Rham spectral sequence for singular varieties are often non-zero. Another consequence is a completely elementary description of Hartshorne's algebraic de Rham cohomology: it is computed by the completed Amitsur complex for any variety in characteristic 0.
arXiv:1009.3108 Sur le topos infinitésimal p-adique d'un schéma lisse I from arXiv Front: math.AG by Alberto Dario Arabia, Zoghman Mebkhout In order to have cohomological operations for de Rham p-adic cohomology with coefficients as manageable as possible, the main purpose of this paper is to solve intrinsically and from a cohomological point of view the lifting problem of smooth schemes and their morphisms from characteristic p > 0 to characteristic zero which has been one of the fundamental difficulties in the theory of de Rham cohomology of algebraic schemes in positive characteristic since the beginning. We show that although smooth schemes and morphisms fail to lift geometrically, it is as if this was the case within the cohomological point of view, which is consistent with the theory of Grothendieck Motives. We deduce the p-adic factorization of the Zeta function of a smooth algebraic variety, possibly open, over a finite field, which is a key testing result of our methods.
Toen: Algebres simplicicales etc, file Toen web prepr rhamloop.pdf. Comparison between functions on derived loop spaces and de Rham theory. Take a smooth k-algebra, k aof char zero. Then (roughly) the de Rham algebra of A and the simplical algebra
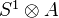determine each other (functorial equivalence). Consequence: For a smooth k-scheme , the algebraic de Rham cohomology is identified with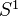 
-equivariant functions on the derived loop space of . Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.