Andre-Quillen cohomology

• General Introduction

  This is somehow "cohomology of commutative rings", in some sense "analogous" to the (Hochschild?) cohomology of associative algebras. The 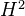should classify extensions in some category of commutative rings.

  <]]>

• Search results

  MathSciNet

  Google Scholar

  Google

  arXiv: Experimental full text search

  arXiv: Abstract search

  <]]>

• Online References

  See article in Milles folder.

  <]]>

• Paper References

  <]]>

• Definition

  <]]>

• Properties

  <]]>

• Standard theorems

  <]]>

• Open Problems

  <]]>

• Connections to Number Theory

  <]]>

• Computations and Examples

  <]]>

• History and Applications

  <]]>

• Some Research Articles

  <]]>

• Other Information

  Abstract of a talk by Milles: André-Quillen cohomology theory of an algebra over an operad. Following the ideas of Quillen and by means of model category structures, Hinich, Goerss and Hopkins have developped a cohomology theory for (simplicial) algebras over a (simplicial) operad. Thank to Koszul duality theory of operads, we describe the cotangent complex to make these theories explicit in the differential graded setting. We recover the known theories as Hochschild cohomology theory for associative algebras and Chevalley-Eilenberg cohomology theory for Lie algebras and we define the new case of homotopy algebras. We study the general properties of such cohomology theories and we give an effective criterium to determine whether a cohomology theory is an Ext-functor. We show that it is always the case for homotopy algebras.

  <]]>

• Comments Posted

  <]]>

• Comments

  Write a comment

  There are no comments.

• General Introduction
• Search results
• Online References
• Paper References
• Definition
• Properties
• Standard theorems
• Open Problems
• Connections to Number Theory
• Computations and Examples
• History and Applications
• Some Research Articles
• Other Information
• Comments Posted
• Comments