Bloch-Ogus cohomology
-
General Introduction
An axiomatic framework for cohomology theories in algebraic geometry. Examples constructed using Sheaf cohomology
Examples
I wrote these examples a long time ago: l-adic cohomology, Singular cohomology, de Rham cohomology, Deligne cohomology, Motivic cohomology, but should the first three really be there?
The universal example is supposed to be Motivic cohomology. See also Motivic homology, Motivic cohomology with compact supports
Morphic cohomology / Topological cycle cohomology, Lawson homology
Deligne cohomology, Deligne homology. See also Absolute Hodge cohomology, Deligne-Beilinson cohomology
<]]> -
Search results
<]]> -
Online References
<]]> -
Paper References
There are several articles of Barbieri-Viale on H-cohomology and other things, in which he uses the formalism of Bloch-Ogus cohomology. See MathSciNet reviews - most of these articles are not online in Feb 2009.
<]]> -
Definition
This is a set of axioms, for details see Levine, page 24.
The axioms describe a functor which to each object of (the big Zariski site)
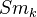 associates a bigraded object
associates a bigraded object 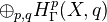 . The axioms require among other things:
. The axioms require among other things:- Some kind of "relative" version for closed subsets of

- A product
- Homotopy invariance
- Purity
- Cycle classes
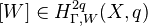 where
where 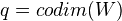
<]]> - Some kind of "relative" version for closed subsets of
-
Properties
<]]> -
Standard theorems
It might be the case that Gersten's conjecture holds for all Bloch-Ogus theories. See section 2.5.7 in Gillet: K-theory and Intersection theory
<]]> -
Open Problems
<]]> -
Connections to Number Theory
Kato defined Bloch-Ogus like complexes for any excellent scheme, see MR0833016
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
The Bloch-Ogus--Gabber Theorem, by Jean-Louis Colliot-Thélène, Raymond T. Hoobler, and Bruno Kahn, K0169:
In this paper, we give an exposition of Gabber's proof of the Bloch-Ogus theorem for étale cohomology with locally constructible torsion coefficients. We then abstract the ingredients of the proof to give an axiomatic treatment of it. The axioms involved are much less demanding than those of Bloch and Ogus and therefore apply to a vaster array of cohomology theories. We also give a detailed treatment of universal exactness à la Grayson, as well as several applications.
This paper has appeared in Fields Institute for Research in Mathematical Sciences Communications Series 16, A.M.S., 1997, 31-94, so the dvi files have been removed. See http://www.fields.utoronto.ca/pubs.html.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.