Chow groups
-
General Introduction
See also Algebraic cycles, Higher Chow groups, Chow homology, Chow groups with coefficients, Chow cohomology
<]]> -
Search results
<]]> -
Online References
Gillet: K-theory and Intersection theory (looks excellent)
Something might be in here.
A very intereting paper by Joshua on motivic DGA.
<]]> -
Paper References
Levine in K-theory handbook.
My own notes from Totaro's course, spring 2008.
Seminaire Chevalley: Anneaux de Chow et applications (1958)
Soulé et al: Lectures on Arakelov Geometry. First chapter treats intersection theory for an arbitrary regular noetherian finite-dimensional scheme.
What about Bloch: An elementary presentation... (in Motives vol)?
<]]> -
Definition
<]]> -
Properties
Homotopy invariance and localization. See Levine (page 443). Also Mayer-Vietoris long exact seq. Products. Projective bundle formula.
The Kunneth formula fails for Chow groups, at least over the complex numbers. Counterexample: See Totaro's Algebraic cycles exam, there one shows that the natural homomorphism
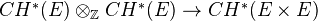is not surjective.<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
Several papers by Akhtar on K-theory archive.
http://mathoverflow.net/questions/99897/examples-of-chow-rings-of-surfaces mentions surfaces over finite fields
arXiv:1207.4703 On the Chow groups of certain geometrically rational 5-folds fra arXiv Front: math.NT av Ambrus Pal We give an explicit regular model for the quadric fibration studied in Pirutka (2011). As an application we show that this construction furnishes a counterexample for the integral Tate conjecture in any odd characteristic for some sufficiently large finite field. We study the étale cohomology of this regular model, and as a consequence we derive that these counterexamples are not torsion.
arXiv:1206.2704 On the torsion of Chow groups of Severi-Brauer varieties fra arXiv Front: math.AG av Sanghoon Baek For a large class of central simple algebras we provide upper bounds for the annihilators of the torsion subgroups of the Chow groups of the corresponding Severi-Brauer varieties.
<]]> -
History and Applications
<]]> -
Some Research Articles
The Chow groups and the motive of the Hilbert scheme of points on a surface, by Mark Andrea de Cataldo and Luca Migliorini: K0415
Saito: On the bijectivity of some cycle maps (in Motives vol)
Pedrini and Weibel: K-theory and Chow groups on singular varieties (1986)
Roberts: Chow's moving lemma. (Appendix to Kleiman's Motives article in the Oslo volume)
Saito et al: We study the higher Chow groups CH^2(X,1) and CH^3(X,2) of smooth, projective algebraic surfaces over a field of char 0.
The oriented Chow ring, by J. Fasel
Chow rings of excellent quadrics, by Nobuaki Yagita: K0787
MR1780429 (2001m:11106) Otsubo, Noriyuki(J-TOKYO) Selmer groups and zero-cycles on the Fermat quartic surface.
Soulé: Groupes de Chow et K-théorie de varietes sur un corps fini (1984)
Biswat and Srinivas: The Chow ring of a singular surface
Kresch: Canonical rational equivalence of intersections of divisors (1999)
Roberts: Recent developments on Serre's multiplicity conjectures: Gabber's proof of the nonnegativity conjecture (1998)
Complex varieties for which the Chow group mod n is not finite (2002)
Laterveer: Algebraic varieties with small Chow groups. Discusses things related to "representability of Chow groups", and the Hodge conjecture.
Green, Griffiths: Formal Deformation of Chow Groups. In Abel volume.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.