Cyclic homology
-
General Introduction
See also Negative cyclic homology
<]]> -
Search results
<]]> -
Online References
For cyclic homology pf schemes, see Weibel, and also K0046 and Keller
For cyclic homology of exact categories, see Keller
Cyclic homology of commutative algebras: Cortinas
Something on cyclic homology of A_infty-algebras, by Khalkhali.
Foliation groupoids and their cyclic homology, by Marius Crainic and Ieke Moerdijk: K0446
Page 33 of Weibel
Puschnigg on excision
cycle category in nlab
Weibel, C.: The Hodge filtration and cyclic homology. Preprint, uiuc K-theory archive (1994)
Various articles of Kaledin might be interesting, including something about coefficients of cyclic homology.
<]]> -
Paper References
Chapter 9 in Weibel: An introduction to homological algebra.
Loday: Cyclic homology. Springer, 1992.
Connes: Noncommutative differential geometry (1985) (online?)
Loday, Quillen: Cyclic homology and the Lie algebra homology of matrices (1984)
Tsygan: Homology of matrix algebras over rings and the Hochschild homology (1983)
Hesselholt in K-theory handbook.
See maybe things in the folder Noncomm geom and Cstar-alg.
Loday: Cyclic homology. In Noncomm geom folder. Covers many aspects of Cyclic and Hochschild homology. Among many other topics: Secondary char classes (section 11.5), Homology of small categories (App C), periodic and negative cyclic homology, Andre-Quillen homology, Deligne cohomology. For the latter, the main point is that there a cyclic homology complex of Connes which computes integral coeffs reduced Deligne cohomology but which has strictly commutative products!! This is stated for smooth algebras over C, not sure if it can be generalized to more general schemes. Also I am not sure if this has any relevance for non-reduced Deligne cohomology.
<]]> -
Definition
<]]> -
Properties
arXiv:1211.1813 Pro excision and h-descent for K-theory fra arXiv Front: math.AG av Matthew Morrow In this paper it is proved that K-theory (and Hochschild and cyclic homology) satisfies pro versions of both excision for ideals (of commutative Noetherian rings) and descent in the h-topology in characteristic zero; this is achieved by passing to the limit over all infinitesimal thickenings of the ideal or exceptional fibre in question.
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
Nistor on the cyclic homology of Hecke algebras
<]]> -
Computations and Examples
<]]> -
History and Applications
Connes defined cyclic homology. I think amother definition was given independently by Loday-Quillen and Feigin-Tsygan, that agrees with Connes' original definition rationally.
<]]> -
Some Research Articles
Kazhdan et al: K0222
Cyclic homology: Various papers by Cortinas, see MR
The obstruction to excision in K-theory and in cyclic homology, by Guillermo Cortiñas: K0524
Cyclic homology, cdh-cohomology and negative K-theory , by Guillermo Cortinas , Christian Haesemeyer , Marco Schlichting , and Charles A. Weibel: K0722
Lodder on comparison with Leibniz homology
Jones: Cyclic homology and equivariant homology (1987)
Kassel: Cyclic homology, comodules, and mixed complexes (1987)
Toen: Algebres simplicicales etc, file Toen web prepr rhamloop.pdf. Comparison between functions on derived loop spaces and de Rham theory. Take a smooth k-algebra, k aof char zero. Then (roughly) the de Rham algebra of A and the simplical algebra
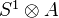 determine each other (functorial equivalence). Consequence: For a smooth k-scheme
determine each other (functorial equivalence). Consequence: For a smooth k-scheme  , the algebraic de Rham cohomology is identified with
, the algebraic de Rham cohomology is identified with 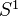 -equivariant functions on the derived loop space of
-equivariant functions on the derived loop space of  . Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]>
. Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]> -
Other Information
Dwyer, Hopkins, Kan: The homotopy theory of cyclic sets. Model structure on the cat of cyclic sets, with a homotopy cat equivalent to that of spaces with a circle action, or to spaces over K(Z, 2). "This places cyclic homology in algebraic topology" or something like that
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.