Deligne cohomology
-
General Introduction
See also: Deligne-Beilinson cohomology, Absolute Hodge cohomology, Deligne homology, Bloch-Ogus cohomology, Pretheory
<]]> -
Search results
<]]> -
Online References
See the chapter by Esnault and Viehweg in the Beilinson volume (on Peter Schneider's web page). See also the excellent article of Scheider himself in the same volume, for more detiailed intro to some of the same things as Deninger-Scholl.
Deninger-Scholl: The Beilinson conjectures. Excellent summary of lots of properties of Deligne cohomology.
<]]> -
Paper References
Burgos-Gil: The regulators of Beilinson and Borel
Levine, in K-theory handbook page 510, mentions real Deligne cohomology and integral Deligne cohomology, and cycle class maps to these cohomologies.
C*-algebras: See many things in the folder Noncomm geom and Cstar-alg. Same for Noncomm geom in the sense of Connes, Cyclic homology
Loday: Cyclic homology. In Noncomm geom folder. Covers many aspects of Cyclic and Hochschild homology. Among many other topics: Secondary char classes (section 11.5), Homology of small categories (App C), periodic and negative cyclic homology, Andre-Quillen homology, Deligne cohomology. For the latter, the main point is that there a cyclic homology complex of Connes which computes integral coeffs reduced Deligne cohomology but which has strictly commutative products!! This is stated for smooth algebras over C, not sure if it can be generalized to more general schemes. Also I am not sure if this has any relevance for non-reduced Deligne cohomology.
LNM 1594: Algebraic cycles and Hodge theory. Contains the following lectures, many of them touching Deligne cohomology in some way:
- Green: Infinitesimal methods in Hodge theory
- Murre: Algebraic cycles and algebraic aspects of cohomology and K-theory
- Voisin: Transcendental methods in the study of algebraic cycles
- Pirola
- Van Geemen: An introduction to the Hodge conjecture for abelian varieties
- Muller-Stach: A remark on height pairings
<]]> -
Definition
Philosophically, absolute Hodge cohomology might be better in some cases. See Schneider bottom of p 8. This may or may not be related to connectivity properties of the representing spectra. Last paragraph of Schneider says that the interpretation of Deligne cohomology as an Ext group is valid for p < 2q, the Ext group being Ext1 from R to
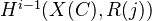.Notes from discussion with Scholl, Nov 2007:
Consider the complex os sheaves
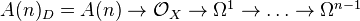
on
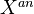. (X is probably a complex variety). Here 
is some ring, and 
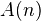is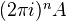 
, I think.We define
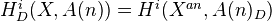. (hypercohomology, I think)See more details in notes from the discussion.
<]]> -
Properties
Deligne cohomology and homology form a twisted Poincaré duality theory in the sense of Bloch and Ogus. See Jannsen.
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
Regulator map!
Note the following version which might be related to a regulator map from etale motivic cohomology: Paulo Lima-Filho, TAMU Integral Deligne cohomology for real projective varieties
We develop an 'integral Deligne cohomology theory' for real varieties which bears to Bredon cohomology the same relation that ordinary Deligne cohomology for complex varieties bears to singular cohomology. The theory has a wide range of connections ranging from equivariant topology (via Bredon equivariant cohomology), through complex differential geometry (via holomorphic line bundles with quadratic forms and holomorphic connections) to number theory (via Milnor K-theory of number fields and regulator maps). We will present --time permitting-- many examples. In a forthcoming work we show that the cycle map from motivic cohomology to Bredon cohomology factors through our Deligne cohomology groups.
In Esnault-Vieweg's survey on Deligne they outline a theory for real varieties, as well. Such a variant would be related to Lichtenbaum's etale motivic cohomology and the Borel version of equivariant cohomology. The difference between their version and ours stems from the difference between the etale and Nisnevich topologies.
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Ayoub and Barbieri-Viale on an algebraic avatar of Deligne cohomology.
There are articles by Lima-Filho on a construction of integral Deligne cohomology, see for example the abstract under Bredon cohomology
MR1273841 (95g:19002) Karoubi, Max(F-PARIS7-M) Classes caractéristiques de fibrés feuilletés, holomorphes ou algébriques. (French. English, French summary) [Characteristic classes of foliated, holomorphic or algebraic bundles] Proceedings of Conference on Algebraic Geometry and Ring Theory in honor of Michael Artin, Part II (Antwerp, 1992). $K$-Theory 8 (1994), no. 2, 153--211.
MR1758580 (2001g:14033) Gajer, Pawe\l(1-JHOP) Geometry of higher connections.
MR2123228 (2005m:14008) Chen, Xi(3-AB); Lewis, James D.(3-AB) The Hodge-$\scr D$-conjecture for $K3$ and abelian surfaces.
<]]> -
Other Information
Possibly the article of Dubois and Jarraud could be interesting. Contains results (\"locally free of finite type and compatible with base change\") about higher direct images of sheaves of differential forms, and also the structure sheaf, assuming certain properties of the morphism.
Deligne cohomology is mentioned at the nLab entry on differential cohomology
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.