Deligne-Beilinson cohomology
-
General Introduction
<]]> -
Search results
<]]> -
Online References
Chapter 10 in the book of Burgos Gil
A chapter in the Beilinson volume: Esnault, Viehweg
<]]> -
Paper References
Soulé MR991985 contains a review of D-B cohomology.
Zucker-Brylinski review some material.
<]]> -
Definition
Brief notes from Esnault-Viehweg
(see link under Online references below)
Deligne cohomology is defined for a complex manifold. Deligne-Beilinson cohomology is defined for a quasi-projective complex manifold, and presumably coincides with Deligne cohomology in the compact/proper case.
We can extend the definition of D-B cohomology to simplicial schemes over
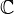(separated, of finite type).There is a cycle class map from the Chow ring to the D-B cohomology ring, which is related to the Abel-Jacobi map.
We can define Chern classes of vector bundles in D-B cohomology.
Beilinson describes D-B cohomology as an extension of Hodge structures.
Brief notes from Burgos Gil, chapter 10.
One considers a proper smooth algebraic varity
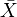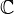over , with a normal crossings divisor D. Put 
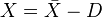. For a subgroup 
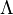of 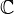one defines a complex of sheaves, in the analytic topology, 
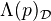(or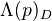 
). The hypercohomology of this sheaf is the Deligne-Beilinson cohomology of 
. Notation: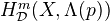 
.Alternative definition in terms of certain complexes. Some Hodge theory; if
is projective, then 
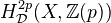is en extension of 
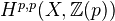by the intermediate Jacobian 
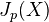.Representation of real D-B cohomology in terms of smooth differential forms.
Definition of D-B cohomology for real varieties.
Remark: "In general it is not clear how to define an integral/rational structure on D-B cohomology. However, when
is defined over a number field one can do something for certain values of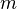 
and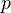 
.Notes from Feliu section 1.4
Description of the truncated Deligne complex (the square of (p,q)-forms with the extra diagonal arrow on top) which computes the Deligne cohomology
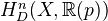of an (open) complex algebraic manifold, in degrees 
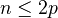. Also description of the product structure in terms of this complex. The only reference is to Burgos Gil: Arithmetic Chow rings and Deligne-Beilinson cohomology. Description of the complex of currentsFunctoriality: Contravariant functoriality by pullback of differential forms (with log singularities). Covariant functoriality for proper morphisms
of equidimensional cplx algebraic manifolds (index shifting).Cohomology with supports. Cycle map from Chow groups as expected.
Chern classes: explicit descriptions of
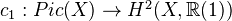and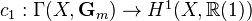 
.For real varieties (i.e. a complex algebraic manifold with an antilinear involution), can compute real D-B cohomology by taking fixed part either of the ordinary D-B cohomology or on the Deligne complex. She actually says that the real D-B cohomology can be computed as the cohomology (not hypercohomology) of the real Deligne complex, but this must be wrong?
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Burgos: Arithmetic Chow rings and Deligne-Beilinson cohomology, 1997.
MR1014822 (90j:14025) Esnault, Hélène(D-MPI) On the Loday symbol in the Deligne-Be\u\i linson cohomology. $K$-Theory 3 (1989), no. 1, 1--28.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.