Elliptic cohomology

• General Introduction

  <]]>

• Search results

  MathSciNet

  Google Scholar

  Google

  arXiv: Experimental full text search

  arXiv: Abstract search

  <]]>

• Online References

  The superb survey by Lurie. Also nlab discussion on this article.

  Some nice slides of Strickland

  http://ncatlab.org/nlab/show/elliptic+cohomology

  http://nlab.mathforge.org/nlab/show/geometric+models+for+elliptic+cohomology

  Folder: Elliptic cohomology, under AT

  <]]>

• Paper References

  Miller and Ravenel, eds.

  Also, at least one other recent book (~ 2007)

  <]]>

• Definition

  <]]>

• Properties

  <]]>

• Standard theorems

  <]]>

• Open Problems

  <]]>

• Connections to Number Theory

  <]]>

• Computations and Examples

  <]]>

• History and Applications

  <]]>

• Some Research Articles

  Three articles on Hecke operators as operations on elliptic cohomology:

  http://www.maths.gla.ac.uk/%7Eajb/dvi-ps/heckop.pdf

  http://www.maths.gla.ac.uk/%7Eajb/dvi-ps/phecke.pdf

  http://www.maths.gla.ac.uk/%7Eajb/dvi-ps/haell.pdf

  Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Notion of derived cat sheaves, a categorification of the notion of complexes of sheaves of O-modules on schemes (also quasi-cohomology and perfect versions). Chern character for these categorical sheaves, a categorified version of the Chern char for perfect complexes with values in cyclic homology. Using the derived loop space. "This work can be seen as an attempt to define algebraic analogues of of elliptic objects and char classes for them". 1. Motivations: Elliptic cohomology, geometric interpretations, chromatic level and n-categorical level, 2-VBs. Maybe the typical generalized CT of chromatic level n should be related to n-cats, more precisely cohomology classes should be rep by maps from X to a certain n-stack. Rognes red-shift conjecture: Intuitively saying that the K-th spectrum of a commutative ring spectrum of chrom level n is of chrom level (n+1). More on ell cohomology and 2-cats. Idea of categorical sheaves: For X a scheme, should have a symmetric monoidal 2-cat Cat(X) which is a categorification of Mod(X), in the sense that Mod(X) should be the cat of endomorphisms of the unit objects in Cat(X). More details. Notions of secondary cohomology and secondary K-theory. Notion of derived categorical sheaves, more reasonable than nonderived version. Relation between 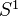-equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.

  Stable bundles over rig categories by Rognes et al, on 2-vector bundles.

  <]]>

• Other Information

  http://mathoverflow.net/questions/101452/what-do-loop-groups-and-von-neumann-algebras-have-to-do-with-elliptic-cohomology

  <]]>

• Comments Posted

  <]]>

• Comments

  Write a comment

  There are no comments.

• General Introduction
• Search results
• Online References
• Paper References
• Definition
• Properties
• Standard theorems
• Open Problems
• Connections to Number Theory
• Computations and Examples
• History and Applications
• Some Research Articles
• Other Information
• Comments Posted
• Comments