Etale cohomology

• General Introduction

  See also Sheaf cohomology, Weil cohomology, l-adic cohomology, Non-standard étale cohomology

  <]]>

• Search results

  MathSciNet

  Google Scholar

  Google

  arXiv: Experimental full text search

  arXiv: Abstract search

  <]]>

• Online References

  My own essay (put this online)

  Milne's online notes

  A great list of links by Bhatt I think.

  http://mathoverflow.net/questions/80633/textbook-for-etale-cohomology

  <]]>

• Paper References

  Tamme

  SGA4 1/2, and SGA4

  Milne's book

  Motives volumes article

  EMS Vol 35 (Alg geom II), ed Shafarevich. Covers cohomology of coherent sheaves and etale cohomology. In Cohomology folder under AG.

  <]]>

• Definition

  <]]>

• Properties

  <]]>

• Standard theorems

  <]]>

• Open Problems

  <]]>

• Connections to Number Theory

  Regarding what happens when p is nnot invertible, see maybe this MO question. http://mathoverflow.net/questions/49887/does-one-need-l-to-be-invertible-in-s-in-order-to-consider-the-l-adic-cohomology

  <]]>

• Computations and Examples

  Jardine: Homotopy and homotopical algebra: The etale cohomology rings of the classifying simplicial schemes 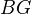fo various group schemes have been calculated. (p. 660)

  <]]>

• History and Applications

  http://mathoverflow.net/questions/6070/etale-cohomology-why-study-it

  http://mathoverflow.net/questions/16195/applications-of-etale-cohomology

  <]]>

• Some Research Articles

  arXiv:1207.3648 Travaux de Gabber sur l'uniformisation locale et la cohomologie etale des schemas quasi-excellents. Seminaire a l'Ecole polytechnique 2006--2008 fra arXiv Front: math.AG av Luc Illusie, Yves Laszlo, Fabrice Orgogozo This book contains notes of a seminar on Ofer Gabber's work on the etale cohomology and uniformization of quasi-excellent schemes. His main results include (cf. introduction) constructibility theorems (for abelian or non-abelian coefficients), vanishing theorems (e.g. affine Lefschetz), uniformization for the "prime-to-l alteration topology", rigidity for non-abelian coefficients, a new proof of the absolute purity conjecture, duality, etc.

  For the Bloch-Ogus-Gabber theorem, see K0169

  Kahn: We prove some finiteness theorems for the \'étale cohomology, Borel-Moore homology and cohomology with proper supports of schemes of finite type over a finite or p-adic field. This yields vanishing results for their l-adic cohomology, proving part of a conjecture of Jannsen.

  K-theory of semi-local rings with finite coefficients and étale cohomology, by Bruno Kahn

  Variations on the Bloch-Ogus Theorem, by Ivan Panin and Kirill Zainoulline: K0556

  Hoobler on the étale and Galois cohomology of semi-local rings

  Probably not so interesting, some thing about mod 2 étale cohomology of real varieties: http://www.springerlink.com/content/x66u20605w22/?p=3c80b59be1374aea82a8a70beebece54&pi=324

  <]]>

• Other Information

  <]]>

• Comments Posted

  <]]>

• Comments

  Write a comment

  There are no comments.

• General Introduction
• Search results
• Online References
• Paper References
• Definition
• Properties
• Standard theorems
• Open Problems
• Connections to Number Theory
• Computations and Examples
• History and Applications
• Some Research Articles
• Other Information
• Comments Posted
• Comments