Etale cohomology of simplicial schemes
-
General Introduction
See stuff on simplicial schemes in my private notes. See also Motivic homotopy theory.
<]]> -
Search results
<]]> -
Online References
Article by Quick?
<]]> -
Paper References
Friedlander: Etale homotopy of simplicial schemes
Deligne: Hodge III
<]]> -
Definition
Def. Etale site of a simplicial scheme. Let
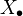be a simplicial scheme. An object in 
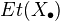is an etale map 
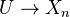for some 
. Maps are commutative squares of the obvious form, where the bottom map 
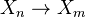is a specified structure map of 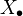. A covering of 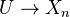is a family 
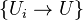of etale morphisms of 
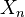-schemes such that the images of the 
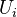cover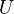 
.(Many more interesting details in Friedlander)
A sheaf is a contravariant functor on
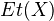satisfying the sheaf condition. This is equivalent to a collection of sheaves 
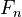on 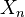satisfying some compatibility criteria.Now etale cohomology is defined in the usual way, as the right derived functors of the "global sections functor". The "global sections functor" here is the map sending a sheaf of abelian groups to the kernel of the map
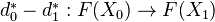. Equivalently,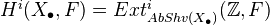 
Can also define etale cohomology of bisimplicial schemes.
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
Can use hypercoverings/Cech cohomology. See Friedlander.
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.