Generalized cohomology
-
General Introduction
The phrase "generalized cohomology" is usually used to refer to a cohomology theory for topological spaces which satisfies the (generalized) Eilenberg-Steenrod axioms. The first such theory to appear, except for "ordinary" (singular) cohomology was topological K-theory.
See also Reduced cohomology
<]]> -
Search results
<]]> -
Online References
<]]> -
Paper References
Kono and Tamaki: Generalized cohomology.
<]]> -
Definition
A generalized cohomology theory is a sequence of functors satisfying axioms I to VI below.
<]]> -
Properties
We present here the Eilenberg-Steenrod axioms, following Kono-Tamaki. Here we consider CW-complexes only, it would probably be better to consider compactly generated spaces.
We consider the category
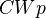 of CW pairs, and the category
of CW pairs, and the category 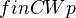 of finite CW pairs. A CW pair is a pair
of finite CW pairs. A CW pair is a pair 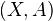 consisting of a CW complex
consisting of a CW complex  and a subcomplex
and a subcomplex  , which can be empty.
, which can be empty.There is a covariant endofunctor
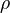 on
on 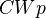 sending
sending 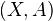 to
to  .
.We consider a sequence of contravariant functors
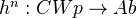 together with natural transformations
together with natural transformations 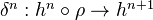 for
for 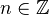 .
.Axioms:
- I, II, III: Functoriality of
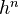 and naturality of
and naturality of 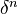
IV (Exactness): For any
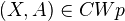 , the following sequence is exact:
, the following sequence is exact: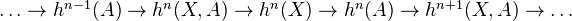
V (Homotopy): Homotopic maps in
 give same map on cohomology
give same map on cohomology- VI (Excision): Let
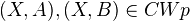 . The inclusion
. The inclusion 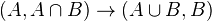 induces an isomorphism on each cohomology group.
induces an isomorphism on each cohomology group. - VII (Dimension):
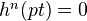 for all nonzero
for all nonzero  .
. - VIII (Additivity): "The cohomology of a disjoint union of spaces is the product of the cohomology of each space"
<]]> - I, II, III: Functoriality of
-
Standard theorems
Any cohomology theory satisfying axioms I - VI above has the following three exact sequences.
We say that
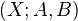 is a triple if
is a triple if 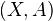 and
and 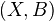 are CW pairs. We say that
are CW pairs. We say that 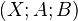 is a triad if
is a triad if 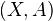 and
and 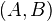 are CW pairs.
are CW pairs.Exact sequence for triple:
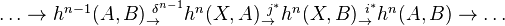
Exact sequence for a triad:
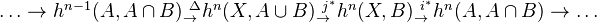
where
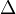 is the excision isomorphism followed by
is the excision isomorphism followed by 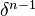 .
.Mayer-Vietoris exact sequence for a triad:
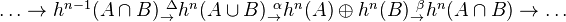
where
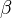 is the difference map, and where
is the difference map, and where 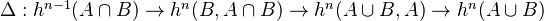 , where the middle map is excision.<]]>
, where the middle map is excision.<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
http://mathoverflow.net/questions/18513/k-theory-as-a-generalized-cohomology-theory
http://mathoverflow.net/questions/29424/difference-between-represented-and-singular-cohomology
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.