Generalized etale cohomology
-
General Introduction
A generalized etale cohomology theory, according to Jardine, is a cohomology theory which is represented by a presheaf of spectra on some étale site. Examples: etale K-theory, etale cohomology.
<]]> -
Search results
<]]> -
Online References
It is not clear to me what the relation is between Jardine's concept and the theories represented by objects in Quick's stable homotopy category.
<]]> -
Paper References
<]]> -
Definition
We follow chapter 6 of Jardine: Generalized etale cohomology theories.
A gen. etale cohomology theory is a graded group
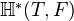, which is associated to a presheaf of spectra 
on an etale site for a scheme 
. It arises from the homotopy category of presheaves of spectra on the underlying site for . If consists of presheaves of Kan complexes, then 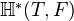is a graded group consisting of morphisms in the associated stable category in the sense that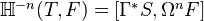
where
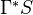is the constant presheaf associated to the ordinary sphere spectrum 
.Formal definition of
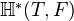in terms of stable homotopy groups of global sections for a globally fibrant model of .Construction of the etale cohomological descent spectral sequence:
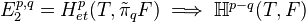
under some hyps. (Use Postnikov resolutions)
Finite approximation technique for computing the groups
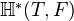
Special case:
is a field. In this the case the category of sheaves on the etale site of can be identified with the classifying topos of the absolute Galois group of . More on generalized Galois cohomology theories.Discussion of Cech cohomology.
Chapter 7: We give proof of Thomason's descent theorem for the Bott periodic K-theory of fields and its corollaries. Outline due to Thomason, but we use homotopy theory of presheaves of spectra (smash products) and the Gabber rigidity theorem.
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.