Group cohomology
-
General Introduction
<]]> -
Search results
<]]> -
Online References
nlab, a bit nonclassical
<]]> -
Paper References
Godement, Sem Bourbaki exp 90: Cohomology of discontinuous groups
Various things in the folder Group and Galois cohomology, including book by Brown and historical survey by MacLane.
Cam Studies in Adv Math 31: Representations and cohomology II, by Benson, excellent. What about vol I??
<]]> -
Definition
One can define group cohomology as a sheaf cohomology. For this, one considers the site given by the canonical topology on the category of left
-sets. Abelian sheaves on this site are equivalent to left -modules. For a left G-module 
, the cohomology group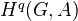 
can be expressed as the sheaf cohomology group 
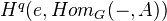, where 
is the one-point set with its unique structure of a left -set. There is also a more general expression for a subgroup of . For continuous group cohomology of a profinite group (Tate cohomology?), one has a similar story. See Tamme p. 55-56, for details.
One can view group cohomology as a functor from modules with a group action to abelian groups. See Baues: Homotopy types, section 5.
There is also a notion of group hypercohomology ("coeffs in a complex of modules").
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
Here is something: K0056
http://mathoverflow.net/questions/37214/why-arent-there-more-classifying-spaces-in-number-theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
http://mathoverflow.net/questions/10879/intuition-for-group-cohomology
http://mathoverflow.net/questions/52099/cohomology-theory-for-algebraic-groups
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.