Higher Chow groups
-
General Introduction
See also Motivic cohomology, Chow groups
<]]> -
Search results
<]]> -
Online References
There is a survey in Levine's book on Mixed motives, available at the AMS site.
Bloch: Some notes on elementary properties of higher Chow groups, including functoriality properties and cubical Chow groups
Suslin: Higher Chow groups and etale cohomology
<]]> -
Paper References
Bloch: Algebraic cycles and higher K-theory (1986)
Bloch: Algebraic cycles and the Beilinson conjectures Google Books link. This paper describes generalized algebraic cycles and higher Chow groups. A preliminary attempt for this was made by Landsburg using hypercubes rather than simplices. See previous paper of Bloch. The new property discussed in the current paper is the construction of cycle classes. If
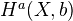 is a nice bigraded CT, e.g. Deligne or
is a nice bigraded CT, e.g. Deligne or 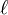 -adic, then there are cycle maps
-adic, then there are cycle maps 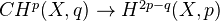 . The higher Chow groups seem to be related to a whole complex of conjectures about K-theory, cycles, and special values of L-functions on arithmetic schemes. Beilinson's conjecture can be reformulated in terms of higher Chow groups. Sheafifyiing the complex of generalized cycles for the etale topology gives a complex satisfying some of the properties conjectured by Lichtenbaum in LNM1068. Soulé's conjecture might be related to some sort of arithmetic index theory for the complex of generalized cycles.
. The higher Chow groups seem to be related to a whole complex of conjectures about K-theory, cycles, and special values of L-functions on arithmetic schemes. Beilinson's conjecture can be reformulated in terms of higher Chow groups. Sheafifyiing the complex of generalized cycles for the etale topology gives a complex satisfying some of the properties conjectured by Lichtenbaum in LNM1068. Soulé's conjecture might be related to some sort of arithmetic index theory for the complex of generalized cycles.Bloch: The moving lemma for higher Chow groups (1994)
Geisser: Basic intersection theory (Appendix to his article in K-theory handbook)
Levine: Bloch's higher Chow groups revisited (1992/1994)
<]]> -
Definition
Note: Groups with coefficients in
 are obtained by tensoring the integral groups with
are obtained by tensoring the integral groups with 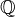 .<]]>
.<]]> -
Properties
<]]> -
Standard theorems
Grayson: (K-th handbook p. 59) Homotopy invariance, localization sequence for an open subscheme and its complement, can be made into a contravariant functor (on nonsingular varieties), and can be compared rationally with K-theory.
Moving lemma implies localization.
André section 18.5:
Bloch introduced higher Chow groups, for smooth varieties. Definition of these.
Thm: For any smooth variety,
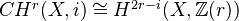 <]]>
<]]> -
Open Problems
arXiv:0909.2670 Beilinson-Tate cycles on semiabelian varieties from arXiv Front: math.AG by Donu Arapura, Manish Kumar Along the lines of Hodge and Tate conjectures, Beilinson conjectured that in the qth cohomology all the weight 2q Hodge cycles of a smooth complex variety and all the weight 2q Tate cycles of a smooth variety over a finitely generated field comes from the higher Chow groups. For product of curves and semiabelian varieties, Beilinson-Hodge conjecture was shown in a previous paper by the authors. Here both Beilinson-Hodge and Beilinson-Tate conjectures are shown to be true for varieties dominated by product of curves. We also show that lower weight Hodge cycles (resp. Tate cycles) are algebraic in these situations.
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
arXiv:1002.2784 On the Grassmannian homology of $\mathbbm{F}2$ and $\mathbbm{F}3$ from arXiv Front: math.KT by Oliver Petras, Dorothee Richters We prove the vanishing of the subgroup of Bloch's cubical higher Chow groups $CH^2(\text{Spec}(\MFp),3)$, $p=2,3$, generated by the images of corresponding projective Grassmannian homology groups ${}^PGH1^2(\MF_p)$ using computer calculations.
<]]> -
History and Applications
<]]> -
Some Research Articles
Müller-Stach and Elbaz-Vincent: Milnor K-theory of rings, higher Chow groups and applications
Geisser: Motivic cohomology over Dedekind rings.
MR2264117 (2007h:14006) Müller-Stach, Stefan J.(D-MNZ-isomorphism) Hodge theory and algebraic cycles. (A survey of recent results)
MR1300893 (95j:11060) Scholl, A. J.(4-DRHM-SL) Extensions of motives, higher Chow groups and special values of $L$-functions. Séminaire de Théorie des Nombres, Paris, 1991--92, 279--292, Progr. Math., 116, Birkhäuser Boston, Boston, MA, 1993.
MR1744946 (2001c:14018) Gordon, B. Brent(1-OK); Lewis, James D.(3-AB) Indecomposable higher Chow cycles. (English summary) The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 193--224, NATO Sci. Ser. C Math. Phys. Sci., 548, Kluwer Acad. Publ., Dordrecht, 2000. 14C30 (14C25 14F43 19E15) PDF Doc Del Clipboard Journal Article Make Link
This is an expository paper focusing on the authors' recent work on representability questions for higher Chow groups. It starts by recalling basic definitions and results concerning Bloch's higher Chow groups, cycle maps into Deligne cohomology and real regulators, as well as decomposability of cycles and the coniveau filtration. Afterwards, it proceeds to a discussion of the main results of [J. D. Lewis, J. Reine Angew. Math. 485 (1997), 161--172; MR1442192 (98i:14008); B. B. Gordon and J. D. Lewis, J. Algebraic Geom. 8 (1999), no. 3, 543--567; MR1689357 (2000d:14003)]. Proofs are not discussed in complete detail but several motivating examples and other background material are included.
MR1906710 (2003i:14005) Collino, Alberto(I-TRIN); Fakhruddin, Najmuddin(6-TIFR-SM) Indecomposable higher Chow cycles on Jacobians. (English summary) Math. Z. 240 (2002), no. 1, 111--139. Extends results of Gordon and Lewis, I think (?)
MR1954824 (2003m:14014) Voisin, Claire(F-CNRS-MJ) Nori's connectivity theorem and higher Chow groups.
MR2282963 (2007k:14004) Chen, Xi(3-AB); Lewis, James D.(3-AB) The real regulator for a product of $K3$ surfaces.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.