Hochschild cohomology
-
General Introduction
<]]> -
Search results
<]]> -
Online References
Brief intro in Caldararu's notes on Derived categories of sheaves, in Homol alg folder or on arXiv.
Schuhmacher: Hochschild cohomology of complex spaces and noetherian schemes, HHA vol 6
Yekutieli: The continuous Hochschild cochain complex of a scheme, Can J Math Vol 54 (6).
<]]> -
Paper References
Short exposition of Hochschild cohomology (for associative algebras) in Ch 11 of Pierce (el), under Algebras.
For cohomology of algebras, see Cartan-Eilenberg, and maybe MacLane: Homology.
Course notes from Grojnowski's lectures in Cambridge.
<]]> -
Definition
This can be regarded as an instance of Monad cohomology.
For Hochschild cohomology of Segal cats and model cats, see Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Idea: Hochschild cohomology should be the space of endomorphisms of an identity functor.
For Hochschild cohomology of DG-categories, see Toen: Lecture on DG-categories. File Toen web unpubl swisk.pdf. Treats basic theory, localization, relation to model cats, functorial cones, K-theory and Hochschild cohomology, and descent problems.
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
arXiv:1102.5756 Cohomology of exact categories and (non-)additive sheaves from arXiv Front: math.KT by Dmitry Kaledin, Wendy Lowen We use (non-)additive sheaves to introduce an (absolute) notion of Hochschild cohomology for exact categories as Ext's in a suitable bisheaf category. We compare our approach to various definitions present in the literature.
Various things by Toen on Hochschild stuff in abstract settings.
arXiv:1001.5379 The homology of digraphs as a generalisation of Hochschild homology from arXiv Front: math.KT by Paul Turner, Emmanuel Wagner J. Przytycki has established a connection between the Hochschild homology of an algebra $A$ and the chromatic graph homology of a polygon graph with coefficients in $A$. In general the chromatic graph homology is not defined in the case where the coefficient ring is a non-commutative algebra. In this paper we define a new homology theory for directed graphs which takes coefficients in an arbitrary $A-A$ bimodule, for $A$ possibly non-commutative, which on polygons agrees with Hochschild homology through a range of dimensions.
Toen: Algebres simplicicales etc, file Toen web prepr rhamloop.pdf. Comparison between functions on derived loop spaces and de Rham theory. Take a smooth k-algebra, k aof char zero. Then (roughly) the de Rham algebra of A and the simplical algebra
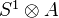 determine each other (functorial equivalence). Consequence: For a smooth k-scheme
determine each other (functorial equivalence). Consequence: For a smooth k-scheme  , the algebraic de Rham cohomology is identified with
, the algebraic de Rham cohomology is identified with 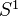 -equivariant functions on the derived loop space of
-equivariant functions on the derived loop space of  . Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.
. Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.Title: Operads of natural operations I: Lattice paths, braces and Hochschild cochains. Authors: Michael Batanin, Clemens Berger and Martin Markl. In this first paper of a series we study various operads of natural operations on Hochschild cochains and relationships between them. http://arxiv.org/abs/0906.4097
<]]> -
Other Information
http://mathoverflow.net/questions/28472/book-on-hochschild-cohomology
http://mathoverflow.net/questions/33877/hochschild-cohomology-of-a-and-of-mod-a
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.