Mixed Tate motives
-
General Introduction
See also Mixed motives
<]]> -
Search results
<]]> -
Online References
Good starting point: Deligne, Goncharov: Groupes fondamentaux motiviques de Tate mixte
Levine?
Bloch: Algebraic cycles and the Lie algebra of Mixed Tate motives, 1991
See also Beilinson, MacPherson, Schechtman, Duke Math J 54
<]]> -
Paper References
<]]> -
Definition
Deligne and Goncharov constructs the cat of MTMs over a number field
with coeffs in the rationals as the heart of a t-structure on on the full triangulated subcat of 
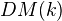generated by Tate objects. The existence of the t-structure follows from the Beilinson-Soulé vanishing conjecture, which holds over a number field thanks to Borel. The authors define mixed Tate motives over the ring of S-integers in as a sub cat of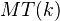 
. More in the paper, and also in the review.<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
arXiv:1102.1312 Mixed Tate motives over $\Z$ from arXiv Front: math.AG by Francis Brown We prove that the category of mixed Tate motives over $\Z$ is spanned by the motivic fundamental group of $\Pro^1$ minus three points. We prove a conjecture by M. Hoffman which states that every multiple zeta value is a $\Q$-linear combination of $\zeta(n1,..., nr)$ where $n_i\in {2,3}$.
arXiv:1110.0923 On p-adic periods for mixed Tate motives over a number field from arXiv Front: math.AG by Andre Chatzistamatiou, Sinan Ünver For a number field, we have a Tannaka category of mixed Tate motives at our disposal. We construct p-adic points of the associated Tannaka group by using p-adic Hodge theory. Extensions of two Tate objects yield functions on the Tannaka group, and we show that evaluation at our p-adic points is essentially given by the inverse of the Bloch-Kato exponential map.
arXiv:1006.4343 Mixed Artin-Tate motives with finite coefficients from arXiv Front: math.CT by Leonid Positselski The goal of this paper is to give an explicit description of the triangulated categories of Tate and Artin-Tate motives with finite coefficients Z/m over a field K containing a primitive m-root of unity as the derived categories of exact categories of filtered modules over the absolute Galois group of K with certain restrictions on the successive quotients. This description is conditional upon (and its validity is equivalent to) certain Koszulity hypotheses about the Milnor K-theory/Galois cohomology of K. This paper also purports to explain what it means for an arbitrary nonnegatively graded ring to be Koszul. Exact categories, silly filtrations, and the K(\pi,1)-conjecture are discussed in the appendices. Tate motives with integral coefficients are considered in the "Conclusions" section.
arXiv:1003.1267 Mixed Artin-Tate motives over number rings from arXiv Front: math.AG by Jakob Scholbach This paper studies Artin-Tate motives over number rings. As a subcategory of geometric motives, the triangulated category of Artin-Tate motives DATM(S) is generated by motives of schemes that are finite over the base S. After establishing stability of these subcategories under pullback and pushforward along open and closed immersions, a motivic t-structure is constructed. Exactness properties of these functors familiar from perverse sheaves are shown to hold in this context. The cohomological dimension of mixed Artin-Tate motives is two, and there is an equivalence of the triangulated category of Artin-Tate motives with the derived category of mixed Artin-Tate motives.
Update in second version: a functorial and strict weight filtration for mixed Artin-Tate motives is established. Moreover, two minor corrections have been performed: first, the category of Artin-Tate motives is now defined to be the triangulated category generated by direct factors of $f_* \mathbf 1(n)$---as opposed to the thick category generated by these generators. Secondly, the exactness of $f^*$ for a finite map is only stated for etale maps $f$.<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.