Mixed motives
-
General Introduction
A category of abelian mixed motives has not yet been constructed, but there are suggestions, by Nori and maybe also by others. For the formalism of mixed motives, see various articles in the Motives volumes.
Specific classes of mixed motives include Mixed Tate motives, 1-motives, Laumon 1-motives.
The triangulated category of mixed motives has been constructed by Voevodsky, see Voevodsky motives. This is supposed to be the derived category of the above-mentioned abelian category. Voevodsky mentions in the introduction to Homology of schemes I, that the abelian category cannot exist when working with integral or finite coeffs (but possibly with rational coefficients), although for finite coeffs it is possible that the triangulated cat of mixed motives is the derived cat of an exact category.
See also Motives, and Motivic cohomology
<]]> -
Search results
<]]> -
Online References
[CDATA[Levine's heavy book.
A better source is probably his recent survey article, published on paper in Handbook of K-theory. See in particular page 28-29 in the online version, or page 456-457 in the paper version.
There is also some notes by Bloch, and the article by Nekovar, and other articles in the Motives volumes.
Deninger: On extensions of mixed motives
For Nori motives, see von Wangenheim: http://front.math.ucdavis.edu/1111.5146
<]]> -
Paper References
The book by André
There are some Springer Lecture notes by Huber. Are these online somewhere?
Jannsen: Mixed motives and algebraic K-theory. LNM 1400.
Beilinson: Height pairings between algebraic cycles. In LNM 1289.
Jannsen: Motivic sheaves and filtrations on Chow groups (Motives vol)
LNM 1604: Mixed motives and their realizations in derived categories
<]]> -
Definition
The theory of mixed motives is still to a large extent conjectural, although constructions have been suggested by Nori, Voevodsky and others.
Some of the properties one hopes for: Let
 be a field. There should exist a rigid tensor category
be a field. There should exist a rigid tensor category 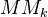 containing "Tate objects"
containing "Tate objects" 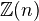 and a functor
and a functor 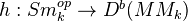 such that one gets a universal Bloch-Ogus theory by setting
such that one gets a universal Bloch-Ogus theory by setting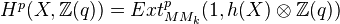
for
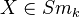 .
.Some further expected properties: The full subcat of semi-simple objects should be equivalent to the category of homological motives, after tensoring with
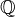 . Structure of neutral Tannakian category (after tensoring with
. Structure of neutral Tannakian category (after tensoring with 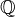 or
or 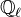 ). Natural weight filtration on each object. Certain isomorphism with K-groups, arising from an Atiyah-Hirzebruch type spectral seq.<]]>
). Natural weight filtration on each object. Certain isomorphism with K-groups, arising from an Atiyah-Hirzebruch type spectral seq.<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
See Toen AIM talk on Homotopy types of algebraic varieties. Towards the end he talks about the motivic schematic homotopy theory, which should be closely related to mixed motives.
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Bloch describes a possible approach to mixed motives in Remarks on elliptic motives
Bloch and Kriz: Mixed Tate motives.
Bruguieres: On a Tannakian result due to Nori (preprint?)
Goncharov: Periods and mixed motives (2002, arXiv)
Nori: Constructible sheaves (2002)
MR1141206 (92m:14012) Saito, Morihiko(J-KYOT-R) Hodge conjecture and mixed motives. I. Complex geometry and Lie theory (Sundance, UT, 1989), 283--303, Proc. Sympos. Pure Math., 53, Amer. Math. Soc., Providence, RI, 1991. Also a follow-up: II.
MR1649192 (99i:19004) Goncharov, Alexander(1-BRN) Volumes of hyperbolic manifolds and mixed Tate motives. J. Amer. Math. Soc. 12 (1999), no. 2, 569--618.
Hanamura: Mixed motives and algebraic cycles I, II, III.
Hanamura: Homological and cohomological motives of an algebraic variety
Masaki Hanamura, The mixed motive of a projective variety (183--193)
Terasoma: Mixed Tate motives and multiple zeta values (Invent., 2002)
arXiv:0911.5611 Réalisations des complexes motiviques de Voevodsky from arXiv Front: math.AG by Florence Lecomte, Nathalie Wach Over a number field k, we construct realizations of Voevodsky motivic complexes, realizations as presented by Fontaine and Perrin-Riou [FPR94]. Our realization functors are defined from the category of motivic complexes constructed by Voevodsky and are obtained as cohomological functors which are, up to some limits, representable. The De Rham realization is represented by the De Rham motivic complex defined in [LW09]. We obtain integral Betti and l-adic realizations. Our realization functors are related by comparison arrows, which become isomorphisms when restricted to the category of geometrical motives. Furthermore, on geometrical motives, the realizations are endowed with Bondarko's weight filtration [Bo09], the Hodge realization is constructed and all these realizations coincide rationally with those defined by A. Huber [H00].
arXiv:1001.5112 Mixed Motives over $k[t]/{(t^{m+1})}$ from arXiv Front: math.AG by Amalendu Krishna, Jinhyun Park For a perfect field $k$, we construct a triangulated category of mixed motives over $k[t]/{(t^{m+1})}$. The ext groups in this category are given by higher Chow groups, and additive higher Chow groups.
<]]> -
Other Information
A general idea is to assume one is given some category M of pure motives and then to try to construct a Hopf algebra or a co-Lie algebra H in the category M such that corepresentations of H in M give rise to (and conjecturally are equivalent to) mixed motives whose weight graded pieces lie in M. The focus becomes the study of H and its representations just as in number theory one studies the Galois group and its representations. In the case of motives, H is constructed using algebraic cycles, and cycle classes in some Weil cohomology lead to realizations of the mixed motives.” Quote from MathSciNet review of an article by Bloch
Voevodsky: Nilpotence theorem for cycles algebraically equivalent to zero. Discusses smash nilpotence, the nilpotence conjectures, and various ideas related to mixed motives, theories of motivic type, the standard conjectures, and stuff about algebraic equivalence, for example mixed motives modulo alg equiv.
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.