Motives
-
General Introduction
This should be converted into a disambiguation page. Look at what comes up on a search and reorganise this introduction, with links to all the (key) types of motives, and a brief explanation of how they fit together. Maybe the same introduction will appear in the book project.
Types of motives: Artin motives, Artin-Tate motives (???), birational motives
For now we only give links to Pure motives and Mixed motives
The references and links below are in a chaos. Structure this when enough understanding.
See also Noncommutative motives
<]]> -
Search results
<]]> -
Online References
Basic/introductory
Barry Mazur: What is a Motive?.
Wikipedia article) on motives.
A very nice introduction by Bruno Kahn, in French.
Another nice introduction by Bloch (also exists in ps format)
A book review by Weibel (of Cycles, transfers and motivic homology theories)
Arithmetic aspects
A survey by Bruno Kahn, from the Handbook of K-theory.
Lectures of Kim and Sujatha at the Asian-French summer school, see also other references
More advanced
Some slides by Kahn on pure motives. Also some slides on motivic Galois groups
A DG Guide to Voevodsky's Motives, by A. Beilinson and V. Vologodsky: K0832
Clozel on automorphic objects corresponding to motives.
Lecture of Levine on Mixed motives and homotopy theory of schemes.
A book by Connes and Marcolli: Noncommutative geometry, quantum fields and motives.
Some nice things can be found towards the end of Jannsen's article on Deligne homology.
<]]> -
Paper References
Some things including Andre and Bloch are found in folder AG/Motives
The two Motives volumes, edited by Jannsen, Kleiman and Serre. These contain for example: Deligne: A quoi servent les motifs? Scholl: Classical motives
Yves Andre: Introduction aux motifs.
For Absolute Hodge cycles: See LNM 900.
Manin: Correspondences, motives and monoidal transformations
M. Demazure, "Motives des variétés algébrique" , Sem. Bourbaki Exp. 365 , Lect. notes in math. , 180 , Springer (1971) pp. 19–38
S.L. Kleiman, "Motives" P. Holm (ed.) , Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970 , Wolters-Noordhoff (1972) pp. 53–96
S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386
Saito: Motives, algebraic cycles and Hodge theory
Demazure: Motifs de varieties algebriques. Bourbaki report (1971)
Saavedra Rivano: Categories tannakiennes. LNM 265, 1972.
Milne: Motives over finite fields (in Motives vol)
<]]> -
Definition
Remark: There might be a notion of motives for stacks. Ref Toen: On motives for DM stacks. Discusses Chow rings and Chow motives, 2 different defs. Motivation: Gromov-Witten invariants.
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
Some Open questions - a summary from a conference in Palo Alto
Standard conjectures
Grothendieck's standard conjectures
Tate conjectures
Tate's Conjecture, algebraic cycles and rational K-theory in characteristic p, by Thomas Geisser. We discuss conjectures on motives, algebraic cycles and K-theory of smooth projective varieties over finite fields. We give a characterization of Tate's conjecture for varieties over finite fields in terms of motives and their Frobenius endomorphism and a criterion in terms of motives for rational and numerical equivalence over finite fields to agree. This together with Tate's conjecture implies that higher rational K-groups of smooth projective varieties over finite fields vanish (Parshin's conjecture). Parshin's conjecture in turn implies a conjecture of Beilinson and Kahn giving bounds on rational K-groups of fields in finite characteristic. We go on to derive further corollaries.
Bloch's conjecture on surfaces?
Bloch/Murre/Beilinson filtration???
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
A computation of a Chow motive: Guletskii and Pedrini
<]]> -
History and Applications
<]]> -
Some Research Articles
André: Pour une théorie inconditionelle des motifs. Publ. Math. IHES, 1996.
Gillet and Soulé: Descent, motives and K-theory
André: Motifs de dimension finie. Bourbaki report, 2004.
André and Kahn: Construction inconditionnelle de groupes de Galois motiviques (2002)
André and Kahn: Nilpotence, radicaux et structure monoidales (2002)
Voevodsky preprint: Motives over simplicial schemes
Construction inconditionnelle de groupes de Galois motiviques, by Kahn and André
Gillet and Soulé: Descent, Motives and K-theory
J-invariant of linear algebraic groups , by Victor Petrov , Nikita Semenov , and Kirill Zainoulline, with nice applications to motivic decompositions. K0805
A note on relative duality for Voevodsky motives, by Luca Barbieri-Viale and Bruno Kahn: K0817
Pure motives, mixed motives and extensions of motives associated to singular surfaces, by J. Wildeshaus: K0856
Weight structures, weight filtrations, weight spectral sequences, and weight complexes (for motives and spectra) , by Mikhail V. Bondarko: K0843
On the multiplicities of a motive , by Bruno Kahn, also K0817
Motives and étale motives with finite coefficients , by Christian Haesemeyer and Jens Hornbostel: K0678
On the derived category of 1-motives, by Luca Barbieri-Viale and Bruno Kahn: K0851 (Aiming towards Deligne's conjectures on 1-motives)
Geometric motives and the h-topology, by Jakob Scholbach: The main theorem of this paper is a reinterpretation of Voevodsky's category of geometric motives: over a field of characteristic zero, with rational coefficients we obtain a description of the category avoiding correspondences by using the h-topology.
Déglise on generic motives
Some abstract stuff, implying that motives of one-dimensional schemes are Kimura finite-dimensional: Guletskii. This is also proved by other means by Mazza
The Geisser-Levine method revisited and algebraic cycles over a finite field, by Bruno Kahn: K0529
Kahn and Sujatha on birational motives
Semenov on a motivic decomposition
Regulators for Dirichlet motives: K0204
Goncharov on mixed elliptic motives: K0228. This is related to work of Wildeshaus in the 90s (elliptic analog of Zagier's conjecture)
Here is something on 1-motives, also something here
Karpenko: construction of the Rost motive
Finite dimensional motives and the conjectures of Beilinson and Murre, by Vladimir Guletskii and Claudio Pedrini: K0617
Crystalline realizations of 1-motives, by F. Andreatta and L. Barbieri Viale: K0620
On the transcendental part of the motive of a surface , by Bruno Kahn , Jacob P. Murre , and Claudio Pedrini: K0759
Morava: On the motivic Thom isomorphism. The existence of a good theory of Thom isomorphisms in some rational category of mixed Tate motives would permit a nice interpolation between ideas of Kontsevich on deformation quantization, and ideas of Connes and Kreimer on a Galois theory of renormalization, mediated by Deligne's ideas on motivic Galois groups.
Wildeshaus on the boundary motive. See also K0708
S. Nikolenko, N. Semenov, and K. Zainoulline
Chow motives of twisted flag varieties, by Baptiste Calmes, Viktor Petrov, Nikita Semenov, and Kirill Zainoulline: K0741
Réalisation l-adique des motifs triangulés géométriques, by Florian Ivorra
Intersection pairing and intersection motive of surfaces, by J. Wildeshaus
Levine's motivic comparison theorem revisited, by Florian Ivorra
Shuji Saito [Shuji Saito1], Motives, algebraic cycles and Hodge theory (235--253)
Sermenev: Motif of an abelian variety (1974)
<]]> -
Other Information
Voevodsky: Homology of schemes I. Discusses the moral of the notion of transfers in the introduction. One of the points seem to be that CTs are functorial wrt correspondences iff they are ordinary, i.e. come from coeffs in a complex of abelian sheaves. Another point is that the "motive" of a CW complex should be its stable homotopy type, if we by motive mean universal wrt all CTs, but if we work with ordinary theories, it should be its singular simplicial complex, as an object in the derived cat of abelian groups. More details provided.
Levine and Krishna explain some construction of homological motives, as the pseudo-abelian hull of a category
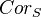, in which the objects are pairs 
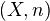of a smooth projective variety and an integer, and there is a functor 
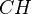sending this object to 
.<]]> -
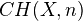Comments Posted
<]]> -
Comments
There are no comments.