Motivic cohomology
-
General Introduction
Motivic cohomology, first envisioned by Beilinson (I think) and then developed by Voevodsky and others in the 90s, has been the subject of much interesting progress. For the material on this page, we are very indebted to sources like Friedlander's Bourbaki article and the book by Mazza/Voevodsky/Weibel.
See also:
Mixed motives, Voevodsky motives, Algebraic K-theory, Motivic homotopy theory
Higher Chow groups, Suslin homology, Homology of schemes, Friedlander-Suslin cohomology, Singular homology of varieties
Motivic cohomology is supposed to be the universal Bloch-Ogus cohomology. See also Motivic cohomology with compact supports, Borel-Moore motivic homology, Borel-Moore homology, Motivic homology
Motivic cohomology is representable in the motivic stable homotopy category; see Motivic homotopy theory.
Motivic cohomology can be viewed as an Absolute cohomology theory.
It is also an Oriented cohomology theory.
Possible the following notions are of some relevance (but maybe not): Pretheory, Mixed Weil cohomology, Twisted duality theory
<]]> -
Search results
<]]> -
Online References
Favourite references:
Mazza, Voevodsky, Weibel: Lectures in motivic cohomology. Most of MVW treats only the case where the base scheme is a field. We have not really taken any notes from MVW in the DB.
Here is what I guess is the orange book, by Friedlander, Suslin and Voevodsky.
Geisser in K-theory handbook (not online)
Friedlander and Kahn (2 articles) in K-theory handbook.
Other references
Voevodsky's Seattle lectures. In Voevodsky folder and probably online.
Levine: Mixed motives. Probably, this is the same as K0107
Levine on lambda operations on K-theory
Something really interesting by May on caterads: here and here
Interesting notes by Friedlander on motivic complexes: K0216
Voevodsky: Motivic cohomology is isomorphic to higher Chow groups.
Geisser: Motivic cohomology over Dedekind rings. Relations to Bloch-Kato and Beilinson-Lichtenbaum.
See also all papers by Voevodsky! Also Suslin, Friedlander.
For the theory of sheaves with transfers, there are nice expositions by Déglise, here and in Nagel and Peters vol I.
Beilinson's original letter
A survey by Niziol on "p-adic motivic cohomology" or motivic cohomology of arithmetic schemes.
<]]> -
Paper References
André: Une introduction aux motifs. My notes
Goncharov in K-theory handbook, for various motivic complexes.
Lichtenbaum: Motivic complexes (in Motives vol). Read again!
<]]> -
Definition
There is a description of motivic Eilenberg-MacLane spaces in Voevodsky ICM talk, using the right analogue of the Dold-Thom construction in topology.
Memo notes from Friedlander: Motivic complexes (K-theory handbook)
Beilinson predicted that motivic cohomology should arise as the cohomology of certain complexes. There are several different suggestions for such complexes.
Suslin complexes ("algebraic singular complexes???")
Motivation: a theorem of Dold-Thom describing the singular cohomology of a topological space group completion of a simplicial abelian monoid built from symmetric products of the space.
Start with a scheme of finite type over a field
 . We have symmetric products
. We have symmetric products 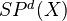 , also of finte type over
, also of finte type over  . We let
. We let 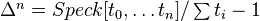 , and let
, and let 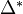 be the corresponding cosimplicial scheme. We define the Suslin complex
be the corresponding cosimplicial scheme. We define the Suslin complex 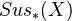 to be the chain complex associated to the simplicial abelian group
to be the chain complex associated to the simplicial abelian group 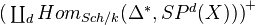 . (Plus denotes group completion)
. (Plus denotes group completion)Important aspects of the Suslin complex:
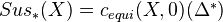 for a certain Nisnevich sheaf
for a certain Nisnevich sheaf 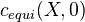 on
on  . This sheaf is actually a presheaf with transfers.
. This sheaf is actually a presheaf with transfers.- Write
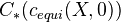 for the complex of Nisnevich sheaves with transfers defined by
for the complex of Nisnevich sheaves with transfers defined by 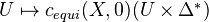 . The homology presheaves of this complex are homotopy invariant
. The homology presheaves of this complex are homotopy invariant
Theorem: Let X be a quasi-projective scheme over an algebraically closed field
 , and let
, and let  be a positive integer relatively prime to the exponential characteristic of
be a positive integer relatively prime to the exponential characteristic of  . Then the mod
. Then the mod  cohomology of
cohomology of 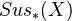 , i.e. the cohomology of the complex
, i.e. the cohomology of the complex 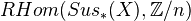 , is given by
, is given by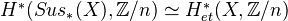
Proof: Uses rigidity theorem of Suslin and Voevodsky, and a comparison between cohomology in the qfh topology and the etale topology.
Nisnevich sheaves with transfers
A motivating fact:
Theorem: Assume
 is a perfect field. Let
is a perfect field. Let 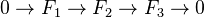 be a short exact sequence of Nisnevich sheaves with transfers (on
be a short exact sequence of Nisnevich sheaves with transfers (on 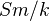 ). Then the resulting triple of chain complexes of abelian groups
). Then the resulting triple of chain complexes of abelian groups 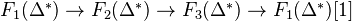 is a distinguished triangle, so determines a long exact sequence of homology groups.
is a distinguished triangle, so determines a long exact sequence of homology groups.Corollary: Let
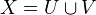 be a covering of a scheme of finite type over a perfect field
be a covering of a scheme of finite type over a perfect field  . Then
. Then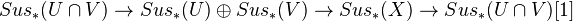
is a d.t.
Now to the definitions. Let
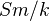 be the category of smooth schemes over
be the category of smooth schemes over  (so in particular of finite type over
(so in particular of finite type over  ). We have the Nisnevich topology on this category. One key property: Points are Hensel local rings.
). We have the Nisnevich topology on this category. One key property: Points are Hensel local rings.We want to talk about singular schemes which admit resolutions by smooth schemes. For this purpose we introduce the stronger cdh topology on
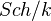 (schemes of finite type over
(schemes of finite type over  ). This is the minimal Grothendieck topology for which Nisnevich coverings are coverings, and also proper surjective morphisms of the following type:
). This is the minimal Grothendieck topology for which Nisnevich coverings are coverings, and also proper surjective morphisms of the following type: 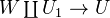 where
where 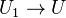 is a closed embedding and
is a closed embedding and 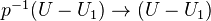 is an isomorphism.
is an isomorphism.We say that a field admits resolution of singularities if
- For any
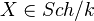 there is a proper birational surjective morphism
there is a proper birational surjective morphism 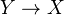 such that
such that 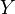 is smooth over
is smooth over  .
. - For any smooth scheme
 over
over  and any proper, birational, surjective map
and any proper, birational, surjective map 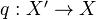 , there exists a sequence of blowups
, there exists a sequence of blowups 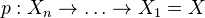 with smooth centers such that
with smooth centers such that 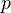 factors through
factors through 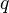 .
.
We define a presheaf
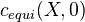 by assigning to
by assigning to 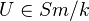 the free abelian group on the set of integral closed subschemes on
the free abelian group on the set of integral closed subschemes on 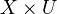 which are finite and surjective over
which are finite and surjective over 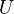 . It is a sheaf for the etale and the Nisnevich topologies. It can be constructed as a sheaf even for the qfh topology, by taking the sheaf associated to the presheaf sending
. It is a sheaf for the etale and the Nisnevich topologies. It can be constructed as a sheaf even for the qfh topology, by taking the sheaf associated to the presheaf sending 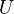 to the free abelian group on
to the free abelian group on 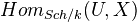 .
.We also define the Nisnevich sheaf
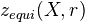 by sending a connected smooth scheme
by sending a connected smooth scheme 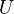 to the group of cycles on
to the group of cycles on 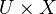 equidimensional of relative dimension
equidimensional of relative dimension  over
over 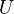 . If
. If  is proper over
is proper over  , then
, then 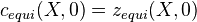 .
.One reason to consider the Nisnevich and cdh topologies rather than the Zariski topology is the existence of Mayer-Vietoris, localization, and blow-up exact sequences. Exact statements, see page 1087 of Friedlander in K-theory handbook.
Def:
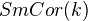 : Objects are smooth schemes over
: Objects are smooth schemes over  , and morphisms are given by
, and morphisms are given by 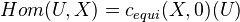 , the free abelian group of finite correspondences from
, the free abelian group of finite correspondences from 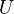 to
to  . A presheaf with transfers is a contravariant
. A presheaf with transfers is a contravariant 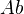 -valued functor on this category.
-valued functor on this category.Note: Earlier papers use condition "pretheory of homological type" on a presheaf. This condition is implied by existence of transfers.
Notation: For a presheaf
 on
on 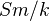 , write
, write 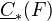 for the complex of presheaves on
for the complex of presheaves on 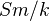 sending
sending 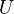 to the complex
to the complex 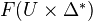 .
.Lemma: Let
 be a presheaf on
be a presheaf on 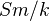 . Consider
. Consider 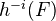 , the presheaf sending
, the presheaf sending 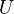 to the
to the 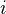 -th homology of
-th homology of 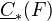 (for some non-negative integer
(for some non-negative integer 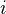 ). Then
). Then 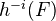 is homotopy invariant.
is homotopy invariant.Theorem: (Rigidity thm) Let
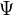 be a homotopy invariant presheaf with transfers satisfying
be a homotopy invariant presheaf with transfers satisfying 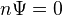 for some
for some  prime to the residue characteristic of
prime to the residue characteristic of  . Let
. Let 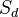 be the henselization of affine
be the henselization of affine 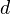 -space at the origin. Then
-space at the origin. Then 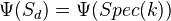 .
.Theorem: Let
 be a homotopy invariant presheaf with transfers. Then its associated Nisnevich sheaf
be a homotopy invariant presheaf with transfers. Then its associated Nisnevich sheaf 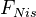 is also a homotopy invariant presheaf with transfers, and equals (as a presheaf on
is also a homotopy invariant presheaf with transfers, and equals (as a presheaf on 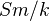 ) the associated Zariski sheaf
) the associated Zariski sheaf 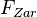 . Moreover, if
. Moreover, if  is perfect, then
is perfect, then 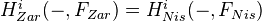
for any
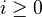 , and these are homotopy invariant presheaves with transfer.
, and these are homotopy invariant presheaves with transfer.Proposition: Assume that
 is perfect, admitting resolution of singularities. Let
is perfect, admitting resolution of singularities. Let  be a homotopy invariant presheaf with transfers. Then for any smooth scheme of finite type over
be a homotopy invariant presheaf with transfers. Then for any smooth scheme of finite type over  ,
, 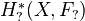 is independent of the topology
is independent of the topology 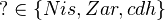
The triangulated category
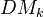
In Voevodsky's approach to motives for smooth schemes and for schemes of finite type over a field admitting resolution of singularities, there is a triangulated category
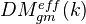 of effective geometric motives. Roughly speaking, this category is by adjoining kernels and cokernels of projectors to the localization of the homotopy category of bounded complexes on the category of smooth schemes and finite correspondences. Inverting the Tate object
of effective geometric motives. Roughly speaking, this category is by adjoining kernels and cokernels of projectors to the localization of the homotopy category of bounded complexes on the category of smooth schemes and finite correspondences. Inverting the Tate object 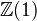 in this category, one obtains the triangulated category
in this category, one obtains the triangulated category 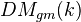 of geometric motives.
of geometric motives.Here, we'll focus on another triangulated category of Voevodsky, here denoted by
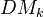 (Voevodsky writes
(Voevodsky writes 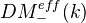 ) The category of effective geometric motives embeds as a full triangulated subcat of
) The category of effective geometric motives embeds as a full triangulated subcat of 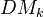 . Also, under this embedding the Tate motive is quasi-invertible, so
. Also, under this embedding the Tate motive is quasi-invertible, so 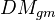 is also a full triangulated subcategory of
is also a full triangulated subcategory of 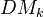 .
.Definition: Let
 be a scheme over a field
be a scheme over a field  . Assume either
. Assume either  smooth, or
smooth, or  of finite type over a field addmitting RoS. Define the motive of
of finite type over a field addmitting RoS. Define the motive of  to be
to be 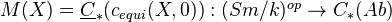
We also define the motive of
 withe compact supports by
withe compact supports by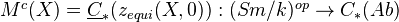
Remark on conventions for complexes:
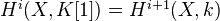
Next: The triangulated category
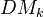 , designed to capture the Nisnevich cohomology of smooth schemes over
, designed to capture the Nisnevich cohomology of smooth schemes over  , and the cdh cohomology of schemes of finite type over
, and the cdh cohomology of schemes of finite type over  .
.Write
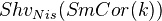 for the category of Nisnevich sheaves with transfers, and consider its derived category (D^{-}, bounded above). Define
for the category of Nisnevich sheaves with transfers, and consider its derived category (D^{-}, bounded above). Define 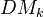 as the subcategory of this derived category consisting of complexes with homotopy invariant cohomology sheaves. Note that the above defined motives are members of this category.
as the subcategory of this derived category consisting of complexes with homotopy invariant cohomology sheaves. Note that the above defined motives are members of this category.Proposition: For
 smooth, we have for any
smooth, we have for any 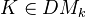 ,
,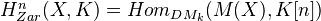
In particular, for
 smooth,
smooth, 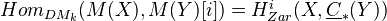
If
 is of finite type over
is of finite type over  , with
, with  admitting RoS, then
admitting RoS, then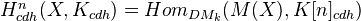
Corollary: If
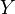 is of finite type over
is of finite type over  , then the homology of
, then the homology of 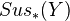 is given by
is given by 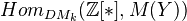 .
.Theorem: Assume
 is a presheaf with transfers on
is a presheaf with transfers on 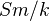 where
where  is perfect and admitting RoS. If
is perfect and admitting RoS. If 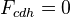 , then
, then 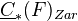 is quasi-isomorphic to
is quasi-isomorphic to 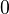 .
.Corollary: Some distinguished triangles for motives (Mayer-Vietoris, localization, blow-ups)
Def: Tate motive, notation
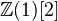 , is the cone of
, is the cone of 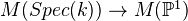 . Also Tate twist:
. Also Tate twist: 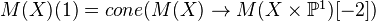 . Same for motives with compact supports.
. Same for motives with compact supports.Remark: One can replace the Nisnevich topology above with the etale topology, and express etale cohomology as a Hom in the corresponding DM category, just as above.
Motivic cohomology and homology
We now define the motivic complexes
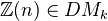 whose cohomology and homology is motivic cohomology and homology. Slightly complicated definition. If
whose cohomology and homology is motivic cohomology and homology. Slightly complicated definition. If  admits RoS, this becomes:
admits RoS, this becomes: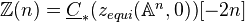
In particular, we get
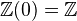 (the constant sheaf) and
(the constant sheaf) and 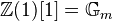
Now let
 be a scheme of finite type over the field
be a scheme of finite type over the field  . We define motivic cohomology of
. We define motivic cohomology of  by
by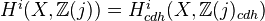
For a positive integer
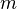 , define mod
, define mod 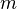 motivic cohomology by:
motivic cohomology by: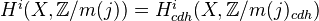
Previous results imply that for
 smooth and
smooth and  perfect, motivic cohomology is Zariski hypercohomology:
perfect, motivic cohomology is Zariski hypercohomology: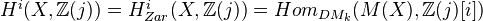
The last term here is also valid when
 admits RoS, for any
admits RoS, for any  of finite type over
of finite type over  .
.Fact: Write
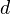 for
for 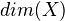 . Then motivic cohomology vanishes for
. Then motivic cohomology vanishes for 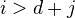 .
.Theorem: For any field
 , and any non-negative integer
, and any non-negative integer  , there is a natural isomorphism:
, there is a natural isomorphism: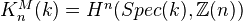
Hence motivic cohomology is defined using the Zariski site, for smooth schemes, and the cdh topology for more general schemes. Using the etale topology instead, one obtains etale motivic cohomology.
Def of motivic cohomology with compact supports, motivic homology, and motivic homology with locally compact supports. Duality and relation to bivariant theory.
Theorem: There is a natural isomorphism with Bloch's higher Chow groups:
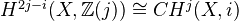
Theorem: Let
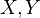 be schemes of finite type over a field
be schemes of finite type over a field  admitting RoS. Then the natural map
admitting RoS. Then the natural map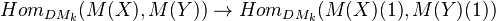
is an isomorphism.
<]]> -
Properties
<]]> -
Standard theorems
Voevoedsky: Cancellation theorem, file in Voevodsky folder, Jan 2002. Proves that if k is a perfect field, than for any
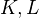 in
in 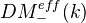 , the map
, the map 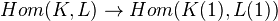 is bijective. This was earlier known when k admits RoS (in Triangulated cats of motives over a field), and also for any field in the case where
is bijective. This was earlier known when k admits RoS (in Triangulated cats of motives over a field), and also for any field in the case where 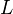 is a shift of a motivic complex (in Motivic cohomology are isomorphic to higher Chow groups).
is a shift of a motivic complex (in Motivic cohomology are isomorphic to higher Chow groups).Voevodsky: Motivic cohomology are isomorphic to higher Chow groups. Shows that two defs (MVW version and SF version I think)of motivic cohomology agree, and that they agree with higher Chow groups for smooth varieties, and that the Cancellation theorem holds, both statements for any base field, without RoS assumption. A nice discussion of the different versions of motivic complexes.
From MVW intro: Homotopy invariance, Mayer-Vietoris and Gysin long exact sequences, projective bundle thm, blowup triangles, and a list of comparison results, see p vi.
http://mathoverflow.net/questions/28856/the-motivic-cohomology-of-projective-space
<]]> -
Open Problems
arXiv:1002.0105 Parshin's conjecture and motivic cohomology with compact support from arXiv Front: math.KT by T. Geisser We discuss Parshin's conjecture on rational K-theory over finite fields and its implications for motivic cohomology with compact support.
Beilinson-Lichtenbaum conjecture
The Beilinson-Lichtenbaum conjecture predicts that the conjectural map of spectral sequences from the "motivic" spectral sequence (motivic cohomology to algebraic K-theory mod-
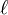 ) to the Atiyah-Hirzebruch spectral sequence (etale cohomology to etale K-theory mod-
) to the Atiyah-Hirzebruch spectral sequence (etale cohomology to etale K-theory mod-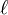 ) should be an isomorphism on
) should be an isomorphism on 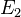 -terms (except for a fringe effect related to mod
-terms (except for a fringe effect related to mod 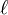 etale cohomological dimension of
etale cohomological dimension of  ).
).The point of this would be to reduce the computation of mod
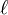 algebraic K-theory to of smooth schemes to topological invariants which in many cases are known.
algebraic K-theory to of smooth schemes to topological invariants which in many cases are known. The Bloch-Kato conjecture for a field
 and a prime
and a prime 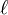 (invertible in
(invertible in  ) implies the Beilinson-Lichtenbaum conjecture for
) implies the Beilinson-Lichtenbaum conjecture for  and
and 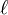 .
.This has lead to (Kahn, Weibel, Rognes) computations of the 2-primary part of rings of the K-theory of rings of integers in number fields.
Nekovar in Motives, page 558: Beilinson conjectures that rational motivic cohomology (and the regulator) extends to the cat of motives mod homological equivalence. (As shown, it does extend to Chow motives).
<]]> -
Connections to Number Theory
For motivic cohomology over arithmetic schemes, Annette Huber said various things, maybe most importantly that there is something by Faltings defining the motivic cohomology of a scheme over say Z as the image in the thing over Q under that map induced by a model. This should give independence of model I think. Ref to a Bourbaki talk, maybe by Faltings. Also ref to "f-motivic cohomology". All this should be related to Scholbach's motives over Z.
http://londonnumbertheory.wordpress.com/2010/02/25/to-add-to-the-study-group-talk-yesterday/
<]]> -
Computations and Examples
Motivic cohomology of smooth cellular varieties, by Kahn
Ben Williams computes motivic cohomology of Stiefel varieties, in some paper (2011).
Oriented Cohomology and Motivic Decompositions of Relative Cellular Spaces , by Alexander Nenashev and Kirill Zainoulline
Motivic cohomology of linear varieties: Joshua, see also K0331
A computation by Walker
<]]> -
History and Applications
Some kind of application by Kahn
<]]> -
Some Research Articles
Voevodsky: On the zero slice of the sphere spectrum. Talks among other things about the slice filtration and about a certain model for the E-M spectrum, which only is valid over a field of characteristic zero.
arXiv:1207.3121 Opérations de Steenrod motiviques fra arXiv Front: math.AT av Joël Riou This article fills some gaps in Voevodsky's construction of the Steenrod operations acting on the motivic cohomology with coefficients in Z/lZ of motivic spaces in the sense of Morel and Voevodsky over a perfect field of characteristic different from l. Moreover, as a consequence of the method of proof of a theorem by Voevodsky on stable cohomology operations, we show that the spectrum that represents motivic cohomology with coefficients Z/lZ has no nonzero "superphantom" endomorphism.
Voevodsky and Suslin: Bloch-Kato conj and motivic cohomology with finite coeffs, file in Voevodsky folder. Contains lots of material on Nisnevich sheaves with transfers and other foundational matters.
Shuji Saito research summary, he has written on motivic cohomology of arithmetic schemes, in particular on finiteness results
Suslin: Algebraic K-theory and motivic cohomology (1995)
Suslin: On the Grayson spectral sequence (preprint 2002)
Suslin, Voevodsky: Bloch-Kato conjecture and motivic cohomology with finite coefficients (2000)
Kahn and Huber: In this paper we study the "slice filtration" defined by effectivity conditions on Voevodsky's triangulated motives, and apply it to obtain spectral sequences converging to their motivic cohomology. These spectral sequences are particularly interesting in the case of mixed Tate motives as their E_2-terms then have a simple description. We apply this in particular to get spectral sequences converging to the motivic cohomology of a split connected reductive group.
Kahn: We reformulate part of the arguments of T. Geisser and M. Levine computing motivic cohomology with finite coefficients under the assumption that the Bloch-Kato conjecture holds. This reformulation amounts to a uniqueness theorem for motivic cohomology, and shows that the Geisser-Levine method can be applied generally to compare motivic cohomology with other types of cohomology theories.
A paper by Scholl: "In the first part of this paper we use de Jong's method of alterations to contruct unconditionally the `integral' subspaces of motivic cohomology (with rational coefficients) for Chow motives over local and global fields - for the motive of a smooth and proper variety possessing a regular model over the ring of integers of the base field, this coincides with the image of the motivic cohomology of the model in that of the generic fibre."
K-theory and motivic cohomology of schemes, by Marc Levine: K0336
Something on Bloch-Kato, by Geisser and Levine
Wildeshaus on the Eisenstein symbol
Levine on inverting the Bott element
Something (wrong) by Walker
Some characteristic p thing by Levine and Geisser
Coniveau spectral sequence and motivic cohomology of quadrics and classifying spaces, by Nobuaki Yagita
Some work by Déglise: K0764, K0765, K0766
The Gersten conjecture for Milnor K-theory , by Moritz Kerz, implying Levine's generalized Bloch-Kato conjecture
Bigraded equivariant cohomology of real quadrics , by Pedro F. dosSantos and Paulo Lima-Filho: K0785
Walker thesis (1996): Motivic complexes and the K-theory of automorphisms. (Available on microfilm!)
MR1265532 (95h:19001) Bloch, Spencer(1-CHI) An elementary presentation for $K$-groups and motivic cohomology. Motives (Seattle, WA, 1991), 239--244, Proc. Sympos. Pure Math., 55, Part 1, Amer. Math. Soc., Providence, RI, 1994.
MR1715883 (2000i:14013) Collino, Alberto(I-TRIN) Indecomposable motivic cohomology classes on quartic surfaces and on cubic fourfolds. (English summary) Algebraic $K$-theory and its applications (Trieste, 1997), 370--402, World Sci. Publ., River Edge, NJ, 1999.
MR2266890 (2007j:11153) Hornbostel, Jens(D-RGBG); Kings, Guido(D-RGBG) On non-commutative twisting in étale and motivic cohomology.
Geisser: Motivic cohomology over Dedekind rings (2004)
Nisnevich: The completely decomposed topology on schemes and associated descent spectral sequences in algebraic K-theory
Yagita: Note on the mod p motivic cohomology of algebraic groups.
Yagita: Note on motivic cohomology of anisotropic real quadrics. Abstract: In this paper, we compute the mod 2 motivic cohomology
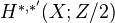 for the anisotropic quadric
for the anisotropic quadric  over
over 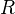 the field of real numbers.
the field of real numbers.Levine and Geisser: The K-theory of fields in char
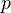 .<]]>
.<]]> -
Other Information
Bloch: Think of a correspondence as
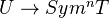
See this MO question for two different versions of motivic cohomology.
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.