Oriented cohomology
-
General Introduction
Examples include algebraic cobordism, algebraic K-theory, and motivic cohomology.
See also Orientable cohomology, Oriented homology, Oriented Borel-Moore homology, Algebraic cobordism
<]]> -
Search results
<]]> -
Online References
See references under Algebraic cobordism. The main reference is the book by Levine and Morel
Push-forwards in oriented cohomology theories of algebraic varieties, by Ivan Panin and Alexander Smirnov: K0459. A sequel is in Panin
<]]> -
Paper References
<]]> -
Definition
<]]> -
Properties
(Following Levine-Morel p. 14) Fix a base scheme
 . Write
. Write 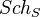 for separated schemes of finite type over
for separated schemes of finite type over  . Write
. Write 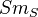 for the full subcat of smooth quasiprojective
for the full subcat of smooth quasiprojective  -schemes. A full subcat
-schemes. A full subcat 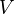 of
of 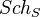 is admissible if it satisfies: 1. It contains
is admissible if it satisfies: 1. It contains  and the empty scheme. 2. If
and the empty scheme. 2. If 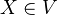 and
and 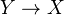 is quasi-projective, then
is quasi-projective, then 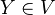 . 3. It is closed under products and disjoint unions.
. 3. It is closed under products and disjoint unions. Definition of transverse morphisms
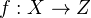 and
and 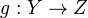 . Def of additive functor from
. Def of additive functor from 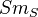 to category of commutative, graded rings with unit: a contravariant functor taking
to category of commutative, graded rings with unit: a contravariant functor taking 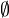 to
to 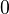 and disjoint unions to products.
and disjoint unions to products.Let
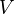 be admissible. An oriented cohomology theory on
be admissible. An oriented cohomology theory on 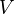 is given by:
is given by:- An additive functor
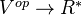
- For each projective morphism
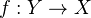 in
in 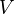 of relative codimension
of relative codimension 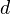 , a HM of graded
, a HM of graded 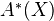 -modules
-modules 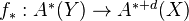
satisfying the following:
- Reasonable behaviour of push-forward wrt identity and compositions.
- For a pullback square given by two transverse morphism
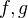 , with
, with  projective of relative dimension
projective of relative dimension 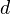 , one has the commutation relation
, one has the commutation relation 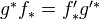 .
. - (PB) Let
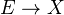 be a rank
be a rank  VB over some
VB over some 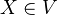 . Then
. Then 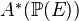 is a free
is a free 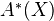 -module, with a certain explicit basis.
-module, with a certain explicit basis. - (EH) Let
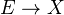 be a VB over some
be a VB over some 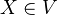 and let
and let 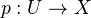 be an
be an 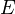 -torsor. Then
-torsor. Then 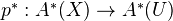 is an isomorphism.
is an isomorphism.
The abbreviations for points 3 and 4 stand for Projective Bundle formula and Extended Homotopy property.
Now suppose the base scheme is a field. Can use Grothendieck's method to define Chern classes
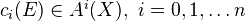 , for a rank
, for a rank  vector bundle
vector bundle 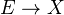 . The first Chern class of a tensor product of line bundles is given by a commutative formal group law over
. The first Chern class of a tensor product of line bundles is given by a commutative formal group law over 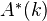 .
.Example: The Chow ring
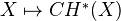 is an oriented cohomology theory on
is an oriented cohomology theory on 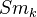 . We have
. We have 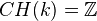 and the formal group law is the additive FGL.
and the formal group law is the additive FGL.Example: The Grothendieck group
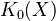 of locally free coherent sheaves is a ring with multiplication induced from tensor product. The functor
of locally free coherent sheaves is a ring with multiplication induced from tensor product. The functor 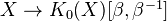 is an oriented cohomology theory. The group law is the multiplicative FGL:
is an oriented cohomology theory. The group law is the multiplicative FGL: 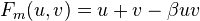 .
.In characteristic zero, the Chow ring functor is the universal ordinary OCT on
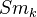 . A rational analogue holds over any field. Examples of ordinary cohomology theories: l-adic cohomology, de Rham cohomology over a field of char zero, the even part of Betti cohomology associated to a complex embedding of the base field. In some sense the universality of the Chow ring explains the cycle class map in all these theories.
. A rational analogue holds over any field. Examples of ordinary cohomology theories: l-adic cohomology, de Rham cohomology over a field of char zero, the even part of Betti cohomology associated to a complex embedding of the base field. In some sense the universality of the Chow ring explains the cycle class map in all these theories.Over any field, the K-group functor described above is the universal multiplicative and periodic OCT on
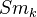 .
.Theorem: Assume
 has characteristic zero. Then there exists a universal oriented cohomology theory on
has characteristic zero. Then there exists a universal oriented cohomology theory on 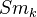 , denoted by
, denoted by 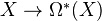 , which we call algebraic cobordism. This universality means what you think it means.
, which we call algebraic cobordism. This universality means what you think it means.Levine-Morel claims (p. 24) that any oriented bigraded theory
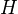 (Bloch-Ogus???) gives an oriented theory, by the formula
(Bloch-Ogus???) gives an oriented theory, by the formula 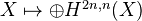 .<]]>
.<]]> - An additive functor
-
Standard theorems
<]]> -
Open Problems
In characteristic zero, the Chow ring functor is the universal ordinary OCT on
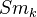 . Conjecture: This holds over any field.
. Conjecture: This holds over any field.Would it make sense to define algebraic cobordism over a field of char zero? Is resolution of singularities the problem?
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
Oriented Cohomology and Motivic Decompositions of Relative Cellular Spaces , by Alexander Nenashev and Kirill Zainoulline
<]]> -
History and Applications
<]]> -
Some Research Articles
Panin and Yagunov on Poincaré duality
Something interesting by Merkurjev
Panin on Riemann-Roch: K0552
Nenashev on Gysin maps
Borel-Moore Functors and Algebraic Oriented Theories , by Mona Mocanasu
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.