Pretheory

• General Introduction

  See Voevodsky. Add links to examples. Maybe these include Algebraic Morava K-theory

  <]]>

• Search results

  MathSciNet

  Google Scholar

  Google

  arXiv: Experimental full text search

  arXiv: Abstract search

  <]]>

• Online References

  Voevodsky: Homology of schemes II, might be the best reference. In particular, there is a long list of examples of pretheories on pp23. This list is a wide selection of CTs, including etale cohomology, alg Kth, algebraic de Rham cohomology, qfh-sheaves, functors representable in DM, Suslin homology, bivariant algebraic cycle homology, higher Chow groups if we could prove functoriality wrt arbitrary (not nec flat) morphisms of schemes, bivariant morphic homology, singular cohomology, the functor taking a complex variety to a MHS, all "derived" cohomology theories like Deligne cohomology etc. Further ideas from this article: Most results restricted to the case of smooth schemes over a base which is a field. For any pretheory with values in an abelian category, can construct an associated family of homotopy invariant pretheories. Particular applications: algebraic cycle homology, bivariant morphic homology, algebraic singular homology, algebraic Lawson homology. A main theorem states roughly that if F is a homotopy invariant pretheory over a perfect field, with values in abelian groups, then the functors 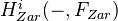have canonical structures of homotopy invariant pretheories. Similar but more general theorem for Nis topology. Also stuff on the etale topology, including a rigidity theorem. This rigidity thm says: A sheaf in the etale topology on Sm/k associated with a homotopy invariant pretheory with values in TAb is locally constant. Here TAb is torsion abelian groups of torsion prime to char(k). Get comparison between etale and Zariski cohomology after tensoring with Q, over a perfect field.

  <]]>

• Paper References

  <]]>

• Definition

  Zainoulline, should perhaps be replaced by K0567

  <]]>

• Properties

  <]]>

• Standard theorems

  <]]>

• Open Problems

  <]]>

• Connections to Number Theory

  <]]>

• Computations and Examples

  <]]>

• History and Applications

  <]]>

• Some Research Articles

  <]]>

• Other Information

  <]]>

• Comments Posted

  <]]>

• Comments

  Write a comment

  There are no comments.

• General Introduction
• Search results
• Online References
• Paper References
• Definition
• Properties
• Standard theorems
• Open Problems
• Connections to Number Theory
• Computations and Examples
• History and Applications
• Some Research Articles
• Other Information
• Comments Posted
• Comments