Reduced cohomology
-
General Introduction
See also Generalized cohomology
<]]> -
Search results
<]]> -
Online References
<]]> -
Paper References
<]]> -
Definition
<]]> -
Properties
See Generalized cohomology for some notation.
A reduced cohomology theory is a sequence of functors
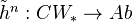 together with natural transformations
together with natural transformations 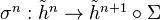 , satisfying the following axioms:
, satisfying the following axioms:- IV' (Exactness): For any inclusion
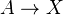 in
in 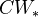 , the sequence:
, the sequence:
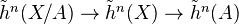 is exact
is exact - V' (Homotopy): Homotopic morphisms in
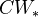 induce the same map on cohomology
induce the same map on cohomology - VI' (Suspension): For
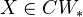 , the map
, the map 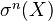 is an isomorphism for all
is an isomorphism for all  .
.
We can also consider an additivity axiom, saying that "the cohomology of a wedge product is the product of the individual cohomology groups".
<]]> - IV' (Exactness): For any inclusion
-
Standard theorems
The reduced cohomology theories are in bijection with the generalized cohomology theories under composition with the functor from CW pairs to
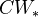 sending
sending 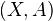 to
to 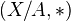 .
.If a map of pointed CW complexes induces an isomorphism on ordinary homology, then it also induces an isomorphism on any reduced cohomology theory. If the complexes involved are finite, the same holds for ordinary cohomology.
(Milnor exact sequence): For a theory satisfying additivity, we have, for any nested union
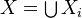 , an exact sequence
, an exact sequence
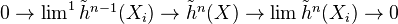
Roughly, the following is true: A cohomology theory on finite CW complexes is determined by its Coefficient group, and the same is true for a theory on CW complexes, provided it satisfies additivity.
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.