Sheaf cohomology
-
General Introduction
Sheaf cohomology can mean several different things. For sheaf cohomology in the sense of Hartshorne, see Zariski cohomology. Here we will describe the more general notion of sheaf cohomology with respect to any Grothendieck topology. As a special case of this, one can also talk about sheaf cohomology of topological spaces (Cartan and others).
In the book project, sheaf cohomology is for the time being included in the "Pure" chapter, because of its usefulness in constructing some Weil cohomology theories. See also the chapter on basic tools/techniques for cosntructing cohomology theories.
Examples: Etale cohomology, Crystalline cohomology, Zariski cohomology, Flat cohomology, l-adic cohomology, Nisnevich cohomology, cdh-cohomology. and cohomology with respect to any other Grothendieck topology, such as the h-topology or the qfh-topology.
See also Cech cohomology and Cohomology with compact supports
<]]> -
Search results
<]]> -
Online References
May on operads and sheaf cohomology
nLab, not much content as of March 2009. See also sheaf, and abelian sheaf cohomology
<]]> -
Paper References
The main source for this page is Tamme: Introduction to Etale Cohomology.
Grothendieck's Tohoku paper is really nice
A pre-Grothendieck standard reference on sheaf cohomology and spectral sequences is Godement 1958: Topologie Algebriques et Theorie des Faisceaux.
B. Iversen, Cohomology of sheaves, Universitext, Springer-Verlag, Berlin, 1986.
M. Kashiwara, P. Schapira, Sheaves on Manifolds, Grundlehren der Mathematichen Wissenschaften 292, Springer-Verlag, 1990.
Various other things in the Homological algebra folder
<]]> -
Definition
We consider a Grothendieck topology
 .
. The category
 of presheaves of abelian groups on
of presheaves of abelian groups on  is abelian and has enough injectives. Any section functor
is abelian and has enough injectives. Any section functor 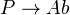 is representable. For a functor
is representable. For a functor 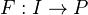 , the inductive limit exists, and is computed "pointwise". The functor
, the inductive limit exists, and is computed "pointwise". The functor 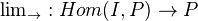 is additive and left exact. If
is additive and left exact. If 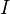 is pseudofiltered, it is exact.
is pseudofiltered, it is exact. By standard results of homological algebra, th right derived functors exist for each left exact functor from
 into an abelian category. Any section functor on
into an abelian category. Any section functor on  is exact, so the derived functors vanish.
is exact, so the derived functors vanish. Cech cohomology associated to a covering
Let
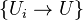 be a covering. Consider the functor
be a covering. Consider the functor 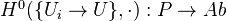 , defined by:
, defined by: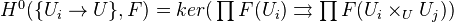
This functor is additive and left exact, and we define Cech cohomology groups associated to the covering
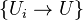 , with values in
, with values in  , by
, by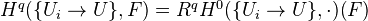
Sheaf cohomology
If
 is a sheaf, the sheaf condition implies that
is a sheaf, the sheaf condition implies that 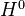 above is equal to
above is equal to 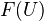 . Hence any section functor
. Hence any section functor 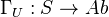 factors through
factors through  via
via 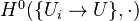 and the natural inclusion functor
and the natural inclusion functor 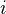 . Such a section functor is left exact, and its right derived functors
. Such a section functor is left exact, and its right derived functors 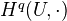 are the cohomology groups with values in abelian sheaves.
are the cohomology groups with values in abelian sheaves.A spectral sequence
Recall Grothendieck's general spectral sequence for composition of left exact functors. When it exists (see Tamme p. 33 - for what topologies are these conditions satisfied?), it takes the following form in the current situation:
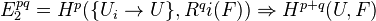
The Cech cohomology groups can be determined by means of Cech cochains, see Tamme p. 33.
Cech cohomology
We can define a category of coverings of an object
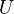 by taking morphisms to be refinement maps (Tamme p. 37). We define Cech cohomology of
by taking morphisms to be refinement maps (Tamme p. 37). We define Cech cohomology of 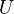 with values in the abelian group
with values in the abelian group  , by
, by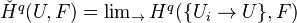
The limit is taken over the category of coverings. As on might expect, we have the following theorem: The functor
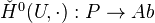 is left exact and additive. Its right derived functors are given by the Cech cohomology groups.
is left exact and additive. Its right derived functors are given by the Cech cohomology groups.Note:
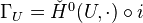 <]]>
<]]> -
Properties
<]]> -
Standard theorems
We begin by developing some theory of sheaves and presheaves. All sheaves are sheaves of abelian groups, unless otherwise specified. Let
 be a Grothendieck topology, and
be a Grothendieck topology, and  ,
,  the categories of abelian presheaves and sheaves, respectively.
the categories of abelian presheaves and sheaves, respectively. Presheaves
Consider two topologies
 and
and 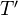 , and a functor
, and a functor 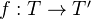 on the underlying cats. Any abelian presheaf
on the underlying cats. Any abelian presheaf 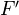 on
on 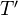 defines a presheaf
defines a presheaf  on
on  by
by 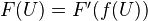 .
. Thm: This construction defines a functor
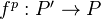 which is additive and exact, and commutes with inductive limits. It admits a left adjoint
which is additive and exact, and commutes with inductive limits. It admits a left adjoint 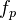 , which is right exact, additive, and commutes with inductive limits. In case
, which is right exact, additive, and commutes with inductive limits. In case 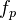 is exact, then
is exact, then 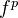 maps injective objects to injective objects. (for proof, see Tamme p. 42)
maps injective objects to injective objects. (for proof, see Tamme p. 42)Remark: Similar result for presheaves of sets.
The functor
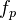 applied to a representable presheaf gives something which is representable by the obvious object.
applied to a representable presheaf gives something which is representable by the obvious object.Example:
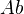 can be identified with the category of presheaves on the topology with underlying category
can be identified with the category of presheaves on the topology with underlying category 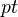 consisting of one object and one identity morphism. Let
consisting of one object and one identity morphism. Let 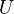 be an object in a topology
be an object in a topology  , and consider the functor
, and consider the functor 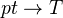 which maps the unique object to
which maps the unique object to 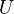 . We get what must be the constant presheaf functor from
. We get what must be the constant presheaf functor from 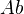 to
to  .
.Sheaves
Thm: The inclusion functor
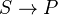 admits a left adjoint, the "sheafification functor".
admits a left adjoint, the "sheafification functor".Proof: The proof uses the left exact functor
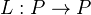 , defined by
, defined by 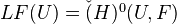 . This functor sends presheaves to separated presheaves (meaning the first part of the sheaf condition sequence is injective) and separated presheaves to sheaves.
. This functor sends presheaves to separated presheaves (meaning the first part of the sheaf condition sequence is injective) and separated presheaves to sheaves.Thm: The category
 is an abelian category satisfying Ab5, and it has generators. The inclusion functor
is an abelian category satisfying Ab5, and it has generators. The inclusion functor 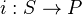 is left exact and the sheafification functor is exact.
is left exact and the sheafification functor is exact.Proof: As for the Zariski topology, one shows that a presheaf kernel is in fact a sheaf, and that the sheafification of a presheaf cokernel is a cokernel in
 . Direct sum is constructed by sheafifying the presheaf direct sum. Likewise, generators are obtained by sheafifying generators for
. Direct sum is constructed by sheafifying the presheaf direct sum. Likewise, generators are obtained by sheafifying generators for  .
.Cor: The category
 has enough injectives.
has enough injectives.Cor: Let
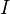 be a category. Every inductive limit (indexed by
be a category. Every inductive limit (indexed by 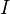 ) exists in
) exists in  . It is equal to the sheafification of the presheaf
. It is equal to the sheafification of the presheaf 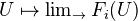 . The functor
. The functor 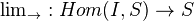 is right exact. It is exact if
is right exact. It is exact if 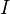 is pseudofiltered.
is pseudofiltered.Cohomology
Any section functor
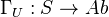 is left exact, being the composition of the left exact inlusion functor, and the exact section functor on
is left exact, being the composition of the left exact inlusion functor, and the exact section functor on  . Since
. Since  has enough injectives, the right derived functors exist, and we define the q-th cohomology group of
has enough injectives, the right derived functors exist, and we define the q-th cohomology group of 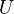 with values in
with values in  by
by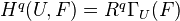
Alternative notation includes the topology T among the arguments, or the final object of
 , in case it exists. Question: Is cohomology functorial in
, in case it exists. Question: Is cohomology functorial in  ???
???Spectral sequences for Cech cohomology
Recall the factorization
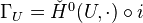 of the section functor
of the section functor 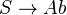 . We introduce the notation
. We introduce the notation 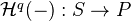 for
for 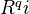 .
. Prop: For each abelian sheaf, we have a canonical isomorphism:
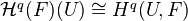 .
.Prop: Recall the functor
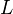 from the proof above. For each abelian sheaf
from the proof above. For each abelian sheaf  we have
we have 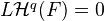 for
for 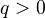 . More explicitly, we have
. More explicitly, we have 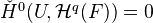 .
.Thm: Let
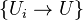 be a covering. For each
be a covering. For each 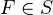 , there is a spectral sequence,
, there is a spectral sequence,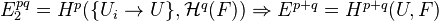
functorial in
 . The same statement holds if replace the initial term by
. The same statement holds if replace the initial term by 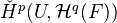 .
. Cor: If
 is a sheaf and
is a sheaf and 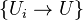 is a covering such that
is a covering such that 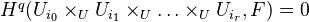 for all
for all 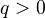 and all finite products of
and all finite products of 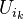 's, then the edge morphisms
's, then the edge morphisms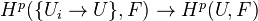
are IMs for all
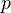 .
. Cor: For all abelian sheaves
 the edge morphism
the edge morphism 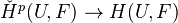 is bijective for
is bijective for 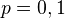 and injective for
and injective for 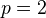 . This can be generalized ("shifted").
. This can be generalized ("shifted").Remark: The above spectral sequence yields as a special case the Hochschild-Serre spectral sequence for an open normal subgroup of a profinite group (Tamme p. 61).
Flabby sheaves
Def: An abelian sheaf is called flabby if
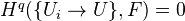 for all coverings and all
for all coverings and all 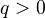 .
.Prop: If a direct sum
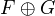 of abelian sheaves is flabby, then
of abelian sheaves is flabby, then  is also flabby. Injective sheaves are flabby. Let
is also flabby. Injective sheaves are flabby. Let 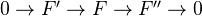 be a short exact sequence in
be a short exact sequence in  . Then: If
. Then: If 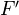 is flabby, the sequence is also exact in
is flabby, the sequence is also exact in  . If
. If 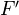 and
and  are flabby, then so is
are flabby, then so is 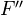 .
.Cor: TFAE:
 is flabby
is flabby- For all
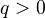 , we have
, we have 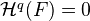 , and therefore
, and therefore 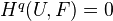
In particular, flabby resolutions in
 can be used to compute
can be used to compute 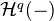 and
and 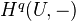 .
.On a given topology
 , all abelian sheaves are flabby iff the inclusion functor
, all abelian sheaves are flabby iff the inclusion functor 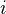 is exact.
is exact.Morphisms between topologies
Consider a morphism
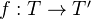 of topologies. We can define additive functors
of topologies. We can define additive functors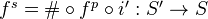
and
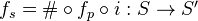
(actually the sheafification
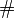 is not needed in the first definition.) These functors can also be defined for sheaves of sets.
is not needed in the first definition.) These functors can also be defined for sheaves of sets.Prop: The functor
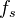 is left adjoint to
is left adjoint to 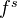 . Hence
. Hence 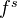 is left exact and
is left exact and 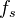 is right exact, and
is right exact, and 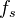 commutes with inductive limits. If
commutes with inductive limits. If 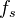 is exact, then
is exact, then 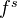 maps injectives to injectives.
maps injectives to injectives.Example: A continuous map
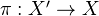 of topological spaces, induces a morphism of topologies
of topological spaces, induces a morphism of topologies 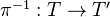 . The functor
. The functor 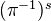 is usually known as the direct image functor
is usually known as the direct image functor 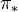 , and the functor
, and the functor 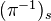 is the inverse image functor.
is the inverse image functor.Thm: Let
 and
and 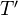 be topologies such that the underlying categories has final objects and finite fibre products. Let
be topologies such that the underlying categories has final objects and finite fibre products. Let 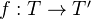 be a morphism of topologies, which respect final objects and finite fibre products. Then
be a morphism of topologies, which respect final objects and finite fibre products. Then 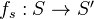 is exact.
is exact.Localization
Let
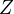 be an object in a topology
be an object in a topology  . Then we can form the topology
. Then we can form the topology 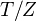 of objects over
of objects over 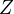 in a natural way, and the natural functor
in a natural way, and the natural functor 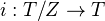 is a morphism of topologies. Lemma: The functor
is a morphism of topologies. Lemma: The functor 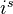 is exact.
is exact.Cor: For all abelian sheaves
 on
on  , there are functorial isomorphisms:
, there are functorial isomorphisms: 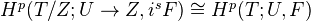
The comparison lemma
Criterion for when a morphism of topologies induces an equivalence between their categories of abelian sheaves, and similar results, such as isomorphism results for the adjoint morphism
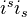 , and exactness criterion for
, and exactness criterion for 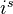 . This yields isomorphism results on cohomology, for "pullback" and "pushforward".
. This yields isomorphism results on cohomology, for "pullback" and "pushforward".Noetherian topologies
Def: An object
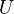 in a topology
in a topology  is called quasi-compact if each covering has a finite subcovering. If every object is quasi-compact, the topology is said to be noetherian.
is called quasi-compact if each covering has a finite subcovering. If every object is quasi-compact, the topology is said to be noetherian.For any topology
 , we can definea new topology
, we can definea new topology 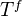 by allowing only finite coverings. If
by allowing only finite coverings. If  is noetherian, get isomorphic cohomology. Also other results on these finiteness issues. (Tamme p. 80)
is noetherian, get isomorphic cohomology. Also other results on these finiteness issues. (Tamme p. 80)Inductive limits of sheaves
In general, the canonical map
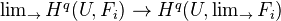 need not be an isomorphism. However, this is the case if
need not be an isomorphism. However, this is the case if  is noetherian and the limit is over a pseudofiltered category. For example, if
is noetherian and the limit is over a pseudofiltered category. For example, if  is noetherian, then cohomology commutes with direct sum of sheaves.<]]>
is noetherian, then cohomology commutes with direct sum of sheaves.<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
See Stillman notes in Homol alg folder
<]]> -
History and Applications
<]]> -
Some Research Articles
Here is an interesting paper: Topological representation of sheaf cohomology of sites, by Carsten Butz and Ieke Moerdijk
<]]> -
Other Information
http://mathoverflow.net/questions/29380/sheaf-cohomology-question
http://mathoverflow.net/questions/32689/how-should-a-homotopy-theorist-think-about-sheaf-cohomology
http://mathoverflow.net/questions/30609/idea-of-presheaf-cohomology-vs-sheaf-cohomology
http://mathoverflow.net/questions/55656/concrete-interpretations-of-higher-sheaf-cohomology-groups
http://mathoverflow.net/questions/11289/geometry-meaning-of-higher-cohomology-of-sheaves
http://mathoverflow.net/questions/13413/interpretation-of-elements-of-h1-in-sheaf-cohomology
http://mathoverflow.net/questions/38966/what-is-sheaf-cohomology-intuitively
http://mathoverflow.net/questions/1151/sheaf-cohomology-and-injective-resolutions
http://mathoverflow.net/questions/28386/the-cohomology-of-a-product-of-sheaves-and-a-plea
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.