Singular cohomology

• General Introduction

  <]]>

• Search results

  MathSciNet

  Google Scholar

  Google

  arXiv: Experimental full text search

  arXiv: Abstract search

  <]]>

• Online References

  Hatcher: http://www.math.cornell.edu/~hatcher/#ATI

  <]]>

• Paper References

  <]]>

• Definition

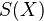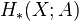  Let be a topological space. Define the singular chain complex . Now and 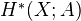is the homology and the cohomology of 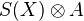and 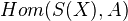, respectively.

  This is a bifunctor, contravariant in and covariant in the coefficient group .

  <]]>

• Properties

  <]]>

• Standard theorems

  <]]>

• Open Problems

  <]]>

• Connections to Number Theory

  <]]>

• Computations and Examples

  <]]>

• History and Applications

  <]]>

• Some Research Articles

  <]]>

• Other Information

  Completely unverified, from MathOverflow: "Singular cohomology of $X$ can be expressed as sheaf cohomology if $X$ is locally contractible and $F$ is the sheaf of locally constant functions."

  <]]>

• Comments Posted

  <]]>

• Comments

  Write a comment

  There are no comments.

• General Introduction
• Search results
• Online References
• Paper References
• Definition
• Properties
• Standard theorems
• Open Problems
• Connections to Number Theory
• Computations and Examples
• History and Applications
• Some Research Articles
• Other Information
• Comments Posted
• Comments