Suslin homology
-
General Introduction
See also Motivic cohomology
<]]> -
Search results
<]]> -
Online References
Levine. In the printed version (K-theory handbook), it is page 446.
Suslin and Voevodsky: Singular homology of abstract algebraic varieties. They also have a few pages on the qfh and h topologies and their sheaves.
Geisser: Suslin's singular homology and cohomology arXiv
<]]> -
Paper References
Suslin: Exposé a la conference de K-théorie, Luminy 1987
<]]> -
Definition
<]]> -
Properties
<]]> -
Standard theorems
André, section 18.5:
Theorem: For
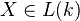 , we have
, we have 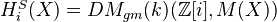 .<]]>
.<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
arXiv:0912.1168 Suslin's singular homology and cohomology from arXiv Front: math.KT by Thomas H. Geisser We discuss Suslin's singular homology and cohomology. In the first half we examine the p-part in characteristic p, and the situation over non-algebraically closed fields. In the second half we focus on finite base fields. We study finite generation properties, and give a modified definition which behaves like a homology theory: in degree zero it is a copy of Z for each connected component, in degree one it is related to the abelianized (tame) fundamental group, even for singular schemes, and it is expected to be finitely generated in general.
Schmidt and Spiess: "In this paper we show that the tamely ramified abelian coverings of smooth, quasiprojective varieties over finite fields can be described in terms of their 0th singular (Suslin) homology. This extends the unramified class field theory of Kato and Saito for smooth, projective varieties over finite fields to the quasiprojective case."
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.