Voevodsky motives
-
General Introduction
See also Mixed motives, Motivic cohomology
Use Friedlander's Bourbaki article.
<]]> -
Search results
<]]> -
Online References
http://ncatlab.org/nlab/show/Voevodsky+motive
Voevodsky: Homology of schemes I. Has a really nice introduction, describing some intuition for the construction of
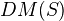, and also about the notion of universal cohomology. See section 4 for construction of DM. Possibly this is improved in later writings and/or by Déglise and Cisinski.For triangulated cats of motives over simplicial schemes, see Voevoedsky: Motives over simplicial schemes. Any simplicial scheme
defines a complex of presheaves with transfers, and hence we can define motivic cohomology of as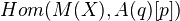 
, taken in the cat 
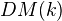or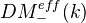 
I think. The main goal of the paper is to define a tensor triang cat 
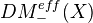such that the motivic cohomology of can be expressed as Hom from the unit object to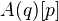 
in this cat. It seems like we always work with simplicial schemes over a perfect field.<]]> -
Paper References
André, chapters 15-17.
<]]> -
Definition
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Huber: Realization of Voevodsky's motives (with a Corrigendum)
Spitzweck: Some constructions for Voevoedsky's triangulated category of motives
In the letter to Beilinson, Voevodsky formulates axioms for a homology theory. He considers
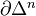as an (n-1)-dim sphere, write also S for the 1-dim sphere in this sense. Let Sch/k be the cat of separated schemes of finite type over a base k. Then a homological theory is a functor from Sch/k together with a family of natural isos 
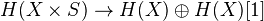. This functor should satisfy some conditions: Morally, homotopy invariance, MV exact triangle, an exact triangle for blowups, and transfer for flat finite morphisms. Get a 2-cat of homological theories over 
. Examples: Algebraic K-th with rational coeffs, l-adic homology, Hodge homology ass to a complex embedding. Thm: There is an initial object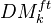 
in this cat, which we call the triang cat of eff mixed motives over k. Notion of reduced homological theory, and reduced motive of a scheme. Any motive in the above sense is of the form 
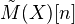, where we may assume affine and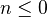 
. Tate object and comparison with K-theory. Bigger cat 
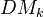which contains the previous as a full triang subcat, but admits a more explicit description rather than just the universal property. Can also be viewed as the closure of the previous, wrt direct sums and inductive limits. Need the h-topology, in particular coverings including surjective blowups, finite surjetive maps, etale coverings. Various filtrations on 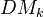(homotopy canonical, geometrical, motivic canonical, weight). The weight filtr should be related to pure numerical motives.<]]> -
Other Information
A fundamental idea in Voevodsky's thesis and in Homology of schemes I, is the homological cat of a site with interval. This might not be so much emphasized for example in MVW, but it seems very natural, and gives some intuition for the def of DM.
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.