Weil cohomology
-
General Introduction
This is the class of cohomology theories for which Pure motives (Chow motives) are supposed to have a universal property.
Examples include: Betti cohomology, Algebraic de Rham cohomology, Crystalline cohomology, l-adic cohomology, Etale cohomology (with finite coefficients), and I think also Rigid cohomology.
See also Primitive cohomology
Weil cohomology theories are used to study Algebraic cycles. Some Weil cohomology theories are constructed using Sheaf cohomology
See also Homotopy type
See also the notion of Mixed Weil cohomology
In the book project, the relevant chapter is the "Pure" chapter.
<]]> -
Search results
<]]> -
Online References
A brief introduction by de Jong
Motivic stuff blog post
<]]> -
Paper References
Kleiman in Motives.
André: Une introduction aux motifs. Especially sections 3.3 and 3.4.
Grothendieck: The cohomology theory of abstract algebraic varieties. 1960 Proc. Internat. Congress Math. (Edinburgh, 1958) pp. 103--118 Cambridge Univ. Press
<]]> -
Definition
<]]> -
Properties
See André for a presentation which differs slightly from Kleiman's below, for example in that André includes Tate twists in the discussion. André also reviews briefly the classical Weil cohomologies. Some notes:
A Weil cohomology is a (symmetric?) monoidal contravariant functor from smooth projective
-schemes to the tensor category of 
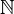-graded vector spaces (finite-dimensional in each degree), such that 
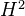of the projective line is one-dimensional. Also two additional requirements (1), (2) below.Tate twist means tensoring with the inverse of the above cohomology space; not that it is invertible in
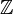-graded vector spaces because it is one-dimensional.The cogebra structure on varieties, induced by the diagonal embedding, induces algebra structure on cohomology.
(1) Duality pairing, trace map
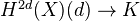
(2) Cycle class map
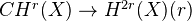
André does not require weak or strong Lefschetz, because these statements lose their relevance when passing from pure to mixed.
A number of formal consequences, including: Various compatibilities, Gysin morphism
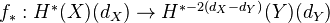
(covariant!), projection formula, description of the trace map, relating Hom of cohomologies to cohomology of product, some stuff about the cycle map (and products, etc), removing of equidimensionality hyp through additivity, Lefschetz trace formula (trivial, from super-linear algebra).
Properties of homological equivalence.
Classical Weil cohomologies. In char zero: Etale cohomology with coeffs in
, 
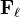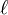-adic cohomology, algebraic de Rham cohomology, Betti cohomology, with their extra structures. In positive char: 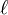-adic cohomology, crystalline cohomology (when is perfect).Comparison IMs, including Tsuji and Berthelot-Ogus. Betti numbers.
Description of the various Tate twists, and of the part of cohomology which receives the cycle map.
Following Kleiman:
A Weil cohomology theory is a contravariant functor from the category of irreducible smooth projective varieties over an algebraically closed field
, to the category of graded anticommutative algebras over a "coefficient field"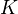 
of characteristic zero, such that the following holds. (Finiteness) Each
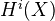has finite dimension, and vanishes unless 
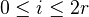, where 
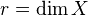.(Poincaré duality) For each
of dimension 
, there is a funcorial "orientation" isomorphism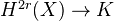 
which, when composed with the multiplication ("cup product") yields a non-degenerate bilinear pairing 
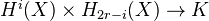. Notation: For a given 
of dimension 
and a map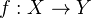 
, we write 
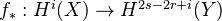for the transpose of 
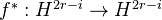.(Kunneth) For all
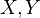, the projections induce an isomorphism 
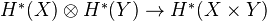.(Cycle map) For each
, write 
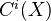for the group of algebraic cycles of codimension 
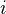. Then there is a group HM 
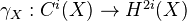satisfying:- (Functoriality) For a map 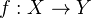, have
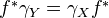and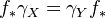 
- (Multiplicativity)
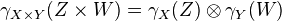
- (Calibration) For a point
, 
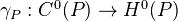is the canonical inclusion of 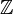into .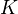
- (Functoriality) For a map
(Weak Lefschetz) Let
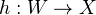be the inclusion of a smooth hyperplane section. Then 
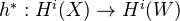is an isomorphism for 
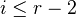and injective for 
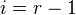.(Strong Lefschetz)
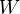as above. Define the Lefschetz operator 
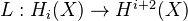by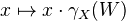 
. Then, for 
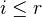,the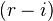 
'th iterate of 
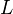is an isomorphism 
.
<]]> -
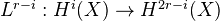Standard theorems
The cycle map preserves products.
If some nonzero multiple of
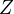is algebraically equivalent to zero, then the cycle map sends 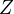to zero.Write
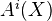for the 
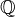-VS generated by the image of the cycle map in 
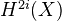. We have
. An element in this set is called a correspondence, and is called algebraic if it lies in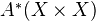 
. Three important kinds of corresponndences: Graph, multiplication, and projector.
Thm: (Trace formula)
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Lubkin: A p-adic proof of Weil's conjectures. Constructs a Weil cohomology for the cat in which an object is a
-variety which lifts to a smooth proper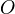 
-scheme. Here 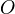is a complete discrete valuation ring with fraction field of char zero and residue field .Macintyre links Weil cohomology to model theory (!) See also Tomasic
<]]> -
Other Information
There is an example of Serre about nonexistence of a cohomology theory with certain properties. Maybe this is related to this SBS post
http://mathoverflow.net/questions/27014/is-it-possible-to-classify-all-weil-cohomologies
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.