de Rham-Witt cohomology
-
General Introduction
<]]> -
Search results
<]]> -
Online References
<]]> -
Paper References
Illusie: Complexe de de Rham-Witt et cohomologie cristalline
<]]> -
Definition
<]]> -
Properties
I think de Rham-Witt theory turns up in the
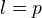case of Bloch-Kato, see this MO answer of Cisinski.<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
<]]> -
Other Information
Dmitry Kaledin (Steklov): Hochschild-Witt complex. Abstract: "de Rham-Witt complex" of Deligne and Illusie is a functorial complex of sheaves WΩ(X) on a smooth algebraic variety X over a finite field, computing the cristalline cohomology of X. I am going to present a non-commutative generalization of this: even for a non-commutative ring A, one can define a functorial "Hochschild-Witt complex" with homology WHH(A); if A is commutative, then WHHi(A)=WΩi(X), X = Spec A (this is analogous to the isomorphism HHi(A)=Ωi(X) discovered by Hochschild, Kostant and Rosenberg). Moreover, the construction of the Hochschild-Witt complex is actually simpler than the Deligne-Illusie construction, and it allows to clarify the structure of the de Rham-Witt complex.
From Thomas: Christopher Davis, a former student of Kedlaya, now in the Bonn MPI, does apparently interesting things with "overconvergent de Rham-Witt cohomology", e.g. a theme in Rogne's seminar this summer. The most readable source shall be Chris' pdh thesis and Kedlaya suggested me to read that (because they want to prove some comparison theorems with that), but apparently Chris does not want to distribute it. Perhaps you are curious about that too and get it. An alternative source could be his paper with Zink and Langer, but far less readable.
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.