l-adic cohomology
-
General Introduction
See also Sheaf cohomology, Weil cohomology, Etale cohomology
<]]> -
Search results
<]]> -
Online References
<]]> -
Paper References
Katz: Review of
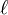 -adic cohomology (in the Motives volumes)
-adic cohomology (in the Motives volumes)Katz: Independence of
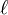 and Weak Lefschetz
and Weak LefschetzTate: Conjectures on Algebraic Cycles in
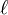 -adic cohomology (in the Motives volumes)<]]>
-adic cohomology (in the Motives volumes)<]]> -
Definition
<]]> -
Properties
<]]> -
Standard theorems
<]]> -
Open Problems
<]]> -
Connections to Number Theory
<]]> -
Computations and Examples
<]]> -
History and Applications
<]]> -
Some Research Articles
Deligne: Decompositions... (Motives vol) has a section.
Ekedahl: On the adic formalism
Kahn: We prove some finiteness theorems for the \'étale cohomology, Borel-Moore homology and cohomology with proper supports of schemes of finite type over a finite or p-adic field. This yields vanishing results for their l-adic cohomology, proving part of a conjecture of Jannsen.
Jannsen: On the $l$-adic cohomology of varieties over number fields and its Galois cohomology. Galois groups over $Q$ (Berkeley, CA, 1987), 315--360.
Jannsen: On the Galois cohomology of $l$-adic representations attached to varieties over local or global fields. Séminaire de Théorie des Nombres, Paris 1986--87, 165--182. Let $K$ be a local or global field, $\overline K$ its separable closure, and $X$ an algebraic variety over $K$. The author presents three conjectures on Galois cohomology of the étale cohomology groups of
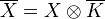 . Statements of conjectures: see Mathscinet - they failed to save.
. Statements of conjectures: see Mathscinet - they failed to save.He states with or without proofs that all conjectures except (1b) are true for $\roman{spec}\,K$ or a form of the standard cellular varieties, that (3) is true for $i=1$, and that (1) holds for $i=1$ if $X$ is an elliptic curve defined over, and having CM by, $K$ and $l$ is a regular prime for $X$.
Analogues of (1) and (3) in the function field case are proved and interrelations between the three conjectures and those of \n A. Be\u\i linson\en [in Current problems in mathematics, Vol. 24 (Russian), 181--238, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984; MR0760999 (86h:11103)] and \n J.-M. Fontaine\en [Ann. of Math. (2) 115 (1982), no. 3, 529--577; MR0657238 (84d:14010)] are discussed.
<]]> -
Other Information
<]]> -
Comments Posted
<]]> -
Comments
There are no comments.