Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- A-infinity algebraWrite comment View comments
http://mathoverflow.net/questions/57589/heuristic-behind-a-infty-algebras
See relevant nLab entries, also A-infinity space, A-infinity operad, A-infinity ring.
http://mathoverflow.net/questions/51817/question-about-a-infty-maps
arXiv:1205.6058 Homotopy unital Ainfinity-algebras fra arXiv Front: math.AT av Volodymyr Lyubashenko It is well known that the differential graded operad of Ainfinity-algebras is a cofibrant replacement (a dg-resolution) of the operad of associative differential graded algebras without units. In this article we find a cofibrant replacement of the operad of associative differential graded algebras with units. Algebras over it are called homotopy unital Ainfinity-algebras. We prove that the operad bimodule of Ainfinity-morphisms is a cofibrant replacement of the operad bimodule of morphisms of dg-algebras without units. Similarly we show that the operad bimodule of homotopy unital A_infinity-morphisms is a cofibrant replacement of the operad bimodule of morphisms of dg-algebras with units.
<]]>- A-infinity categoryWrite comment View comments
[CDATA[See nLab.
Book draft by Seidel on Fukaya categories and Picard-Lefschetz theory, in Symplectic folder. First chapter covers A-infty categories.
<]]>- abc conjectureWrite comment View comments
Rumour, summer 2012 - has the abc conjecture been proven by Mochizuki???
See this review of a Soulé article and the (paper) references it contains for stuff on the Arakelov theory approach to the abc conj via the Bogomolov inequality, and possible solution to the problem of absent absolute differentials. I have the article itself. The notion of successive minima might also be relevant - he mentioned some unpublished preprint with errors from the 90s or so.
http://mathoverflow.net/questions/78061/an-effective-shafarevich-and-the-belyi-degree-of-a-curve
Brief notes in Silverberg: Open questions. In Elliptic curves folder
Various posts on http://www.noncommutative.org/ and maybe other blogs of Lieven. E.g. http://www.neverendingbooks.org/index.php/meanwhile-at-angs.html and http://www.noncommutative.org/index.php/the-abc-conjecture.html
<]]>- Abelian categoryWrite comment View comments
An introduction by Daniel Murfet.
Borceaux vol 2.
http://ncatlab.org/nlab/show/additive+and+abelian+categories
P. Freyd, Abelian categories, Harper, 1966.
[Ga] P. Gabriel, Des categoryégories abéliennes, Bull. Soc. Math. France 90 (1962), 323-448. ONline version exists
Grothendieck's Tohoku paper
An abelian category is an additive category in which every map:
- admits a kernel and a cokernel (Ab1)
- is strict (Ab2)
Recall that a kernel of a morphism
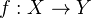is the fiber product 
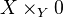. Also recall that a morphism is strict if the natural map from its coimage to its image is an isomorphism.Some properties of abelian cats:
- mono + epi implies iso
- finite limits and colimits exist
- any functor category from a small to an abelian category is abelian
- the opposite of an abelian category is abelian
An abelian category is called semisimple if all short exact sequences split.
A full subcategory of an abelian category is called
- thick if it is closed under kernels, cokernels and extensions.
- generating if "its objects can surject to anything"
- cogenerating if "its objects can "eat" anything", i.e. can receive an injection from any object.
Recall that Hom is left exact in both variables. An object is said to be injective if it is exact as a contravariant functor. An abelian category has enough injectives if the injectives are cogenerating. An object is projective if it is exact as a covariant functor. Enough projectives means that the projectives are generating.
Properties of injective objects: "Any morphism from a subobject to I can be extended to the whole object". (Probably enough for generators). Three facts about short exact sequences: In any short exact sequence, if A, B inj, then C inj. Also, if A inj, then the sequence splits. In a split short exact sequence, B is inj iff A & C are inj.
Freyd-Mitchell thm: Let C be a small abelian category. Then there exists a ring R and an exact fully faithful functor from C to R-mod. (See Kashiwara-Schapira chapter 9)
Some further "axioms" on abelian cats that are sometimes useful to consider (these are not satisfied for all abelian cats):
- All direct sums exist (Ab3)
- (assuming Ab3) "A compatible family of morphisms on an increasingly filtered family of subobjects induce a unique morphism on the sum subobject". (Ab5)
- Also Ab4. See Tohoku
Thm: Let
be abelian, satisfying Ab3. Then direct limits exist in , and the functor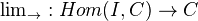 
is additive and right exact. (What is the significance of this result??)
A category is said to be
-linear if the Hom sets are -modules, composition is -linear, and if the category admits finite sums. A functor which respects the -module structure will also respect direct sums, up to a natural isomorphism.<]]>- Abelian varietyWrite comment View comments
Folder: AG/Theta functions (many nice things)
References: Mumford, Milne?
Notes from Tim's course (don't have all pages)
Swinnerton-Dyer: Book on analytic theory, in Elliptic curves folder
http://mathoverflow.net/questions/51955/references-for-abelian-schemes on equations for Jacobians
<]]>- Abstract algebraWrite comment View comments
Berrick and Keating: An introduction to rings and modules with K-theory in view. CUP 2000. (K-th folder)
<]]>- Abstract Brown representabilityWrite comment View comments
See Kashiwara-Schapira.
Hovey suggests the following problem (page 199 of his book). Define "pre-triangulated category with sequential colimits". Show: Every triangulated category gives rise to such a thing. The homotopy category of a model category is such a thing. Define a cohomology functor on such a thing, and prove that all cohomology functors on the homotopy category of a pointed cofibrantly generated model category are representable.
Rosicky: Generalized Brown Representability in homotopy categories (online at TAC), with an erratum here
Raventos and Muro has some project on representability for functors a priori defined only on compact objects, I believe. This could be of interest for example in the case of CTs defined on geometric objects but not a priori on all generalised spaces.
<]]>- Abstract homotopy theoryWrite comment View comments
Cisinski on homotopy theory in toposes. See also other papers by Cisinski.
Cox: Homotopy limits and the homotopy type of functor categories (1976) MR0407022
Jardine on the ideas of Cisinski
Anderson: Axiomatic homotopy theory (1978)
<]]>- Abstract stable homotopy theoryWrite comment View comments
Symmetric powers in stable homotopy cats by Guletskii and Gorchinskiy
<]]>- Accessible categoryWrite comment View comments
- <]]>
- AdamsWrite comment View comments
The selected works of Frank Adams, 2 vols
<]]>- Adams operationsWrite comment View comments
See Feliu thesis
Florence Lecomte, Simplicial schemes and Adams operations
<]]>- Adams spectral sequenceWrite comment View comments
See Adams summary (early in part III).
We consider the stable group
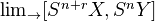for some finite complexes 
and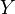 
.The reduced cohomology of
with coefficients in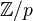 
is a module over the Steenrod algebra 
.The Adams spectral sequence goes from
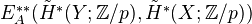
to the above stable group. (What does this mean???)
There is actually a much better and more general formulation of all this. See Chapter 15 in Adams Part III.
<]]>- Additive categoryWrite comment View comments
A category is additive if it satisfies four conditions, including existence of zero object, finite products and coproducts, and "coprod IMic to prod". One proves that a category is additive iff Hom sets are abelian groups, composition is bilinear, and it admits finite products.
http://ncatlab.org/nlab/show/additive+and+abelian+categories
<]]>- Adelic geometryWrite comment View comments
There is a lot of stuff written by Parshin, see for example his Invitation to higher local fields on arxiv. This also contains references to papers by people like Huber and Beilinson, some of which may be difficult to find.
arXiv:0909.1568 Igusa integrals and volume asymptotics in analytic and adelic geometry from arXiv Front: math.NT by Antoine Chambert-Loir, Yuri Tschinkel We establish asymptotic formulae for volumes of height balls in analytic varieties over local fields and in adelic points of algebraic varieties over number fields, relating the Mellin transforms of height functions to Igusa integrals and to global geometric invariants of the underlying variety. In the adelic setting, this involves the construction of general Tamagawa measures.
arXiv:0912.1577 Harmonic analysis on local fields and adelic spaces II from arXiv Front: math.NT by D. V. Osipov, A. N. Parshin This paper is the second part of arXiv:0707.1766. We develope harmonic analysis in some categories of filtered abelian groups and vector spaces over the fields R or C. These categories contain as objects local fields and adelic spaces arising from arithmetical surfaces. Some structure theorems are proven for quotients of the adelic groups of algebraic and arithmetical surfaces.
<]]>- Adelic stuffWrite comment View comments
- <]]>
- Adic spacesWrite comment View comments
See also rigid geometry, analytic space.
Wahle good refs for adic and analytic spaces.
<]]>- Adjoint functorWrite comment View comments
"A left adjoint is right exact"
In general, a left adjoint preserves colimits, and a right adjoint preserves limits.
http://mathoverflow.net/questions/6376/why-forgetful-functors-usually-have-left-adjoint
Examples of adjoints: (left adjoint, right adjoint)
- (geom. realization, sing)
- Lots of examples in Weibel (via index)
- "Informally, a free functor is a left adjoint to a forgetful functor"
<]]>- AdviceWrite comment View comments
Manin: I've had maybe 50 students. 3 or 4 of them failed, all because they insisted on reading. Do mathematics, look at recent arxiv preprints and track back the results you need. Only read what is of immediate use to your research.
Method of poetry: immerse yourself in quality papers
<]]>- Albanese varietyWrite comment View comments
- <]]>
- Algebra over a monoidal categoryWrite comment View comments
Let
be a Monoidal category. A -algebra structure on a category 
is a monoidal structure on 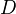together with a monoidal functor 
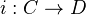. A -algebra functor is a monoidal functor "commuting with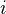 
up to natural isomorphism". The -algebras form a 2-category, and there is a forgetful 2-functor to -modules.Example: Let
be 
-mod (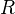 a commutative ring), and consider a map of 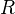-algs, 
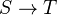. Get a -algebra functor from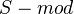 
to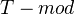 
by tensoring with 
over the base ring 
.If
is symmetric monoidal, then a symmetric -algebra structure on a category 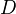is a symmetric monoidal structure on 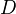together with a symmetric monoidal functor 
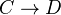. A symmetric -algebra functor is a symmetric monoidal functor that is also a -algebra functor. We can also define a central -algebra structure.Example: The category of modules over a commutative Hopf algebra (over a field) is a central algebra over the category of vector spaces. It is symmetric iff the Hopf algebra is cocommutative.
<]]>- Algebraic categoryWrite comment View comments
nLab "essentially algebraic theory"
nLab on algebraic theory
http://mathoverflow.net/questions/3003/in-what-sense-are-fields-an-algebraic-theory
See also Barr-Beck thm or something like that
Schwede has some notions for triangulated cats I think
Boerceaux vol 2 page 158: A cat equipped with a functor U to sets is called algebraic if (a) it has coequalizers and kernel pairs (b) U has a left adjoint F (c) U reflects isomorphisms (d) U preserves regular epimorphisms (e) UF preserves filtered colimits.
arXiv:1109.1598 Algebraic theories, span diagrams and commutative monoids in homotopy theory from arXiv Front: math.CT by James Cranch We adapt the notion of an algebraic theory to work in the setting of quasicategories developed recently by Joyal and Lurie. We develop the general theory at some length.
We study one extended example in detail: the theory of commutative monoids (which turns out to be essentially just a 2-category). This gives a straightforward, combinatorially explicit, and instructive notion of a commutative monoid. We prove that this definition is equivalent (in appropriate senses) both to the classical concept of an E-infinity monoid and to Lurie's concept of a commutative algebra object.<]]>- Algebraic curveWrite comment View comments
Loads of material on algebraic curves and Riemann surfaces in the folder under AG.
<]]>- Algebraic geometryWrite comment View comments
FGA EGA SGA english index
Add good introductory references. Should include:
Vakil: New revised book/course notes, see his blog.
http://mathoverflow.net/questions/28496/what-should-be-learned-in-a-first-serious-schemes-course
http://mathoverflow.net/questions/1291/a-learning-roadmap-for-algebraic-geometry
http://mathoverflow.net/questions/34110/algebraic-geometry-examples
http://mathoverflow.net/questions/78696/is-there-an-intuitive-reason-for-zariskis-main-theorem
http://mathoverflow.net/questions/111685/on-some-finiteness-properties-for-schemes
Mumford's Red Book
Cox, Little, O\'Shea: Ideals, varieties and algorithms
Dieudonne: History of AG
Putinar and Sullivant ed: Emerging applications of algebraic geometry
FGA, in folder AG/Various. Grothendieck topologies and stacks, Hilbert and Quot schemes, elementary deformation theory, Grothendieck's existence thm in formal geometry, the Picard scheme, summary of intersection theory.
Totaro recommends Lazarsfeld: Positivity
Many useful insights are listed here: http://mathoverflow.net/questions/28496/what-should-be-learned-in-a-first-serious-schemes-course
http://mathoverflow.net/questions/46/what-is-the-universal-property-of-normalization
Bourbaki seminars possibly of some interest:
- Exp 37: Quelques varietes usuelles en G.A.
- exp 49: Hyperplane sections of normal varieties
- Exp 53: Picard vareity and Neron-Severi group
- Exp 71: Serre: Cohomology and complex variables
- Exp 72: Weil on Picard varieties and jacobians
- Exp 75: Equivalence relations on algebraic curves having multiple points
- Exp 66: Neron on arithmetic
- Exp 77: Serre: Cohomology and arithmetic
- Exp 78: Thom on subvarieties and homologu classes of differentiable varieties
- Possibly 84 and 85
- Exp 86: Samuel: Les fonctions holomorphes abstraites de Zariski
- Exp 88: Travaux de Hirzebruch sur la topologie des varietes
- Exp 89: Thom
- Exp 94: The Enriques-Severi Lemma
- Exp 95: Analytic sheaves
- Exp 99: Travaux de Zariski sur Hilbert 14.
Books in the folder AG/Introductory (only the most interesting listed)
- Abhyankar: AG for scientists and engineers. Very down-to-earth, actually quite nice! Goes up to RoS for surfaces and similar things.
- AG1 by Shokurov and Danilov: Basic theory of curves and Jacobians. Basic theory of varieties, some schemes at the end.
- Dieudonne: Algebraic Geometry. Notes in English surveying EGA I-III. (Course notes from Maryland)
- Dieudonne: Fondements de la GA Moderne. Continuation of the Maryland notes. Together these two sets of notes seem like a marvellous route into EGA.
- Dolgachev Topics in Classical AG: Polarity, Conics, Plane cubics, Determinental equations, Theta characteristics, Plane quartics, Planar Cremona transformations, Del Pezza surfaces, Cubic surfaces, Automorphisms of Del Pezzo surfaces, Geometry of Lines.
- Eisenbud-Harris: The geometry of schemes. Excellent book.
- Griffiths-Harris
- Harder: Lectures on AG (Vol 1 out of 3 planned): Basic homological algebra, sheaf theory, cohomology of sheaves, Riemanns surfaces and AVs
- Harris: First course. Classical, no schemes, many examples.
- Hartshorne
- Liu
- Parshin-Shafarevich AG III. Covers Hodge theory, periods, curves and Jacobians.
- Ravi Vakil book project
- Shafarevich ed AG II. Covers cohomology and algebraic surfaces.
- There is one big file with all the Russian AG books (I-V), ed Shafarevich
- Thomas Zeta functions. Contains basic function field arithmetic and some stuff on Weil conjectures.
<]]>- Algebraic geometry examplesWrite comment View comments
Title: Schubert varieties are log Fano over the integers Authors: Dave Anderson, Alan Stapledon http://front.math.ucdavis.edu/1203.6678 Categories: math.AG Algebraic Geometry Comments: 3 pages; to appear in Proc. Amer. Math. Soc MSC: 14M15, 14E30, 20G99 Abstract: Given a Schubert variety Xw, we exhibit a divisor \Delta, defined over the integers, such that the pair (Xw,\Delta) is log Fano in all characteristics.
<]]>- Algebraic groupWrite comment View comments
See Alg groups folder under AG. Many good sources, for example PSPUM-9.
Short article in some Clay volume???
<]]>- Algebraic spaceWrite comment View comments
Ref: Knutson LNM0203.
Algebraic stacks may be viewed as groupoid objects in the category of algebraic spaces. (Joshua: The intersection cohomology...)
http://mathoverflow.net/questions/3194/what-are-the-benefits-of-using-algebraic-spaces-over-schemes
See Toen course in cours folder under Toen, I think around chapters 2 to 4-2 in particular.
http://mathoverflow.net/questions/11226/commutative-rings-to-algebraic-spaces-in-one-jump
<]]>- Algebraic stackWrite comment View comments
See also Stack.
An excellent introduction to derived AG is the CRM 2008 notes, in Toen web unpublished folder. These notes also covers algebraic stacks, the idea of moduli spaces, a little about cotangent complexes, and examples of derived algebraic stacks.
http://mathoverflow.net/questions/73115/query-on-comment-in-deligne-mumford-1969
<]]>- Algebraic surfaceWrite comment View comments
Zariski lectures LNM0083
Folder: AG/Surfaces
http://front.math.ucdavis.edu/0912.4291 Lecture notes on surfaces in positive characteristic
http://mathoverflow.net/questions/40555/calculations-of-pic0-pic-ns-of-surfaces
<]]>- Algebraic topologyWrite comment View comments
General references:
- Books of Hatcher (online)
- The book of May (online)
- Selick: Introduction to homotopy theory
- Many other books in the Alg Top folder!
Also folder under GEOMETRY
A History of Algebraic and Differential Topology, 1900 - 1960 Series: Modern Birkhäuser Classics Dieudonné, Jean 1st ed. 1989. 2nd printing, 2009, XXIV, 648 p., Softcover ISBN: 978-0-8176-4906-7
nLab almost no info at all Aug 09
<]]>- AlgebrasWrite comment View comments
There are loads of different types of algebras around. Start to list here for future ref.
Some introduction is in MacLane: Homology. In Homol alg folder
Skowronski ed: Trends in Representation Theory of Algebras and Related Topics, EMS
Central simple algebras: See Grillet
Jordan algebras: See Bourbaki exp 31
Chiral algebras: See Beilinson book
Hecke algebras
Vertex operator algebras
http://ncatlab.org/nlab/show/von+Neumann+algebra
Book by Chevalley on giga: The construction and study of certain important algebras
<]]>- Almost complex varietyWrite comment View comments
I think Kodaira did important work on almost complex structures, but might be wrong.
Bourbaki exp 35.
<]]>- Almost etaleWrite comment View comments
See Faltings theory folder, under NUMBER TH. Document: almost-etale-stuff
<]]>- Almost rings and schemesWrite comment View comments
- <]]>
- AlterationsWrite comment View comments
Some really really nice things in Resolution of singularities (tribute to Zariski), ed Hauser, Lipman et al. Progress in Mathematics.
An improved version of the alteration thm comes from Gabber's work on purity, see maybe study group notes of Riou or maybe Illusie. Or ask Riou. It was something along the following lines: Take any quite general scheme, and a prime l. Then there exist an alteration of degree prime to l (this is not exactly right, so check proper ref).
http://mathoverflow.net/questions/27821/alterations-of-regular-varieties
The work of Gabber (see Illusie et al on arXiv) contains applications of alterations.
<]]>- Anabelian geometryWrite comment View comments
See lots of material from the Newton Institute programme, fall of 2009. In particular, the presentation of Kim.
Jardine weird quote, I think: Grothendieck fundamental groupoid, leads to anabelian geometry in simplicial (pre?)sheaves
<]]>- Analytic continuationWrite comment View comments
Madhav Nori on analytic continuation and the Poisson formula: http://front.math.ucdavis.edu/1204.3533
<]]>- Analytic geometryWrite comment View comments
Paugam: Global analytic geometry
<]]>- Analytic number theoryWrite comment View comments
Old list of refs:
Article by Shintani on zeta-functions and prehomogeneous vector spaces (related to Sato's work)
Automorphic Forms and L-Functions for the Group GL(n,R). Goldfeld, CUP
Recent Perspectives in Random Matrix Theory and Number Theory. Ed. Mezzadri
Spectral Theory of the Riemann Zeta-Function. Motohashi, CUP
Euler through time... Varadarajan
Dynamical, Spectral, and Arithmetic Zeta Functions/ Lapidus ed.
On Random Matrices, Zeta Functions and Dynamical Systems (Springer, 3-540-23189-7)
Katz and Sarnak: Random matrices, Frobenius eigenvalues, and monodromy.
<]]>- Analytic spaceWrite comment View comments
I think there are real-analytic and complex-analytic spaces.
LNM0025 Narasimhan: Intro to analytic spaces
<]]>- Analytic torsionWrite comment View comments
Burgos talk abstract, Paris, March 2011: The holomorphic analytic torsion classes for Kähler fibrations provide us with a refinement of the Grothendieck-Riemann-Roch theorem at the level of differential forms. They are a key ingredient in the arithmetic Grothendieck-Riemann-Roch theorem. In this talk we will give an axiomatic characterization of holomorphic analytic torsion classes, use it extend analytic torsion classes to arbitrary projective morphisms and extract some consequences. This is joint work with R. Litcanu and G. Freixas.
<]]>- Andre-Oort conjectureWrite comment View comments
See Yafaev and Klingler (arxiv 2012)
Maybe Martin is working on this??
<]]>- AndréWrite comment View comments
- <]]>
- AnelWrite comment View comments
- <]]>
- Anodyne extensionWrite comment View comments
Consider the category of simplicial sets. We define the set
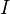as the set of inclusions 
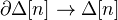for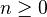 
. Define 
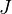to be the set of inclusions 
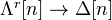for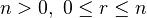 
. A map 
is a cofibration iff it is in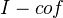 
. A map is a (Kan) fibration iff it is in 
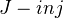. A map is a weak equivalence iff its geometric realization is a weak equivalence of topological spaces. The maps in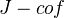 
are called anodyne extensions. See Cofibrantly generated for the notation.Every anodyne extension is a trivial cofibration of simplicial sets.
I think the anodyne extensions include the maps
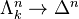. Possibly these suffice for certain "testing".Another formulation: A class of simplicial set monomorphisms is called saturated if contains all IMs, is closed under pushouts, retracts, countable compositions and arbitrary disjoint unions. An anodyne extension is a member of the smallest saturated class which contains the standard inclusions of horns.
Kan fibrations have the RLP wrt all standard inclusions of horns, and hence wrt all anodyne extensions.
<]]>- ArakelovWrite comment View comments
MathSciNet only has four items. I believe there might be other things by Arakelov in Russian.
<]]>- Arakelov theoryWrite comment View comments
An introduction by Burgos-Gil
Lang: Introduction to Arakelov theory
http://www.ncatlab.org/nlab/show/Arakelov+geometry
http://mathoverflow.net/questions/78460/learning-arakelov-geometry
Manin-Panchiskin has some material
Faltings: Calculus on arithmetic surfaces
Gillet in Arcata: Intro to higher-dimensional Arakelov theory
Soulé, Christophe Hermitian vector bundles on arithmetic varieties. Algebraic geometry---Santa Cruz 1995, 383--419, Proc. Sympos. Pure Math., 62, Part 1. This looks excellent, I haven't read it but noted that on p 397 there are references to several attempts to develop adelic intersection theory.
I think Neukirch ANT works out things for Pic-hat of the ring of integers in a number field.
MR1087394 (92d:14016) Gillet, Henri(1-ILCC); Soulé, Christophe(F-IHES) Arithmetic intersection theory. Inst. Hautes Études Sci. Publ. Math. No. 72 (1990), 93--174 (1991). (Long review)
MR1724892 (2000m:14030) Künnemann, Klaus(D-KOLN); Maillot, Vincent(F-ENS-MI) Théorèmes de Lefschetz et de Hodge arithmétiques pour les variétés admettant une décomposition cellulaire. (French)
A course syllabus for a course by Gillet
Vojta: Applications of arithmetic algebraic geometry to Diophantine approximations (1993)
One could maybe look at Bismut, at least the reviews
arXiv:0909.3680 On Volumes of Arithmetic Line Bundles II from arXiv Front: math.AG by Xinyi Yuan For a hermitian line bundle over an arithmetic variety, we construct a convex continuous function on the Okounkov body associated to the generic fibre of the line bundle. The integration of the continuous function gives the growth of the Euler characteristic of the hermitian line bundle. It is the global version of the recent work of Nystrom.
arXiv:1010.1599 Toward Dirichlet's unit theorem on arithmetic varieties from arXiv Front: math.NT by Atsushi Moriwaki In this paper, we would like to propose a fundamental question about a higher dimensional analogue of Dirichlet's unit theorem. We also give a partial answer to the question as an application of the arithmetic Hodge index theorem.
arXiv:1102.2063 Hermitian structures on the derived category of coherent sheaves from arXiv Front: math.AG by José Ignacio Burgos Gil, Gerard Freixas i Montplet, Razvan Litcanu The main objective of the present paper is to set up the theoretical basis and the language needed to deal with the problem of direct images of hermitian vector bundles for projective non-necessarily smooth morphisms. To this end, we first define hermitian structures on the objects of the bounded derived category of coherent sheaves on a smooth complex variety. Secondly we extend the theory of Bott-Chern classes to these hermitian structures. Finally we introduce the category $\oSm_{\ast/\CC}$ whose morphisms are projective morphisms with a hermitian structure on the relative tangent complex.
<]]>- ArapuraWrite comment View comments
- <]]>
- Arf-Kervaire invariantWrite comment View comments
Snaith: Stable homotopy around the Arf-Kervaire invariant (PIM 273) Some background on things like some classical stable homotopy theory, the Arf-Kervaire invariant, Connective K-theory, Algebraic K-theory, MU, KU, BP and more.
<]]>- Arithmetic dualityWrite comment View comments
Deninger: Duality in the etale cohomology of one-dimensional proper schemes and generalizations. Also other papers on Artin-Verdier duality. Artin-V duality for etale cohomology of global fields apparently explains Tate's results on duality in Galois cohomology, which are important in class field theory. See Haberland: Galois cohomology of number fields, for the general number field case. Mazur proved it for totally imaginary quadratic fields. Deninger: function fields, also connections with Poincaré duality.
Milne book
Scholbach: Various things in thesis
arXiv:0910.3759 Étale duality for constructible sheaves on arithmetic schemes from arXiv Front: math.AG by Uwe Jannsen, Shuji Saito, Kanetomo Sato In this note we relate three topics for arithmetic schemes: a general duality for étale constructible torsion sheaves, an étale homology theory, and a Gersten-Bloch-Ogus-Kato complex. The results in this paper have been used in other papers of the authors ([JS], [Sa], [SaH] in the list of references).
arXiv:1102.1302 Geometry of Numbers from arXiv Front: math.AG by Lin Weng We develop a global cohomology theory for number fields by offering topological cohomology groups, an arithmetical duality, a Riemann-Roch type theorem, and two types of vanishing theorem. As applications, we study moduli spaces of semi-stable lattices, and introduce non-abelian zeta functions for number fields.
arXiv:0911.4781 Algebraic K-theory of the fraction field of topological K-theory from arXiv Front: math.KT by Christian Ausoni, John Rognes We compute the algebraic K-theory modulo p and v1 of the S-algebra ell/p = k(1), using topological cyclic homology. We use this to compute the homotopy cofiber of a transfer map K(L/p) --> K(Lp), which we interpret as the algebraic K-theory of the "fraction field" of the p-complete Adams summand of topological K-theory. The results suggest that there is an arithmetic duality theorem for this fraction field, much like Tate--Poitou duality for p-adic fields.
<]]>- Arithmetic geometryWrite comment View comments
Silverberg: Open questions in arithmetic algebraic geometry (2001?)
The book Neron models is great.
Lots and lots of things under NUMBER THEORY not properly indexed (as of March 2009)
Many gems can be found in the MO answers of Emerton
http://mathoverflow.net/questions/61648/local-methods-in-algebraic-number-theory
<]]>- Arithmetic groupWrite comment View comments
Quite a lot seem to be written on cohomology of groups like SL(n, Z), which I guess is an example of an arithmetic group - I have not linked to these papers on K-theory archive. There is something called Eisenstein cohomology of arithmetic groups. Some key names: Borel, Soulé.
PSPUM-9, in Algebraic groups folder.
Milne: Algebraic and arithmetic groups. In Alg gps folder
A few things are in the Arithmetic groups folder under NUMBER THEORY
Book by Borel? There are various introductions and surveys by Borel, see MathSciNet.
Lizhen Ji: Arithmetic groups and their generalizations
A survey by Borel which seems excellent: Armand Borel, Introduction to the cohomology of arithmetic groups (51--86) MR2272919
See also Cohomology of arithmetic groups
http://mathoverflow.net/questions/3701/stable-homology-of-arithmetic-groups
<]]>- Arithmetic homotopyWrite comment View comments
- <]]>
- Arithmetic index theoryWrite comment View comments
This is mentioned on the 5th page (i.e. p 271) of Bloch: Algebraic cycles and higher K-theory. It relates to a conjecture relating orders of zeroes of Hasse-Weil zeta functions to the alternating sum of ranks of higher Chow groups, where the latter can maybe be interpreted as some sort of Euler-Poincaré characteristic for Bloch's complexes.
What could the relation be between this and Kontsevich's very general index theorem?
http://londonnumbertheory.wordpress.com/2009/10/15/computational-class-field-theory/ mentions that Atiyah-Singer is maybe a form of Riemann-Roch.
Minhyong Kim MO comment: I'm sorry to be encouraging random association, but Vojta's proof of Faltings's theorem does use an arithmetic Riemann-Roch theorem, the Archimedean component of which is a refined index theorem. Sorry, couldn't resist.
<]]>- Arithmetic jet spaceWrite comment View comments
arXiv:0908.2512 Differential forms on arithmetic jet spaces from arXiv Front: math.NT by James Borger, Alexandru Buium We study derivations and differential forms on the arithmetic jet spaces of smooth schemes, relative to several primes. As applications we give a new interpretation of arithmetic Laplacians and we discuss the de Rham cohomology of some specific arithmetic jet spaces.
<]]>- Arithmetic mysteriesWrite comment View comments
http://mathoverflow.net/questions/38066/which-languages-could-appear-on-weils-rosetta-stone
http://mathoverflow.net/questions/25975/is-there-an-arithmetic-cobordism-category
The two books of Neukirch contain some useful basics
Can we use for some arithmetic applications, the general philosophy that from the right perspective, everything is affine, and from the right perspective, everything is smooth?
Can we use functoriality wrt correspondences for understanding/computing CTs of arithmetic schemes?
<]]>- Arithmetic schemesWrite comment View comments
Try to understand and gather examples of arithmetic schemes.
Source of examples: Can I get notes from the summer school at EPFL 2012 on del Pezzo and K3 surfaces, by Anthony Várilly-Alvarado?
http://mathoverflow.net/questions/97086/does-smooth-and-proper-over-mathbb-z-imply-rational
Title: Hyperelliptic curves and their invariants: geometric, arithmetic and algorithmic aspects Authors: Reynald Lercier, Christophe Ritzenthaler Categories: math.NT Number Theory (math.AG Algebraic Geometry) Comments: 46 pages ; related programs are available on the web pages of the authors MSC: 14Q05, 13A50, 14H10, 14H37 Abstract: We apply classical invariant theory of binary forms to explicitly characterize isomorphism classes of hyperelliptic curves of small genus and, conversely, propose algorithms for reconstructing hyperelliptic models from given invariants. We focus on genus 3 hyperelliptic curves. Both geometric and arithmetic aspects are considered.
Arithmetic moduli of elliptic curves, by Katz and Mazur
Deninger: l-adic Lefschetz numbers of arithmetic schemes
Asked Jakob Scholbach about whether a scheme over Z which is nonflat must lie over a finite set of primes. Answer: The following is e.g. in Hartshorne: let X be reduced. A map
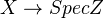is flat iff every irreducible component is dominant over Z, i.e., contains the generic point Spec Q. Actually I was erroneously forgetting the irreducible component (or connected component, since I only look at regular schemes at these places). So, if it is not flat (but reduced and irred.) it cannot be dominant, hence must be a 
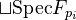- scheme (finite disjoint union of some finite fields). The reducedness is nowhere a problem for me, mainly since 
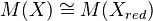by localization, i.e., the motive does not see whether the scheme is reduced or not.Understand relation to log geometry
Shuji Saito research summary. Check also his preprints and publications pages for new preprints, in Sep 2009 he mentions some in preparation.
David Holmes once mentioned a paper related to hyperelliptic genus two curves, and Tate's algorithm, in which they do blowups over Spec Z.
http://mathoverflow.net/questions/9576/smooth-proper-scheme-over-z about smooth proper schemes without sections.
http://mathoverflow.net/questions/20913/families-of-sheaves-on-arithmetic-varieties
http://mathoverflow.net/questions/77546/schemes-over-with-a-graded-existence-over-sub1-sub
All answers of Liu: http://mathoverflow.net/users/3485/qing-liu
Toric varieties
See for example the review of Maillot: Un théorème de Bernstein-Koushnirenko arithmétique (the article is not available online yet, maybe later on Science Direct), for examples of how toric varieties can be viewed as schemes over Z. In the setting of this article, the canonical metric on the Hermitian bundle is not smooth in general, but Maillot overcomes this problem. See also G´eom´etrie d’Arakelov des vari´et´es toriques et fibr´es en droites int´egrables by same author.
Maillot considers cellular arithmetic schemes in Progr Math 171 article, such as toric schemes, flag schemes, and Grassmann schemes over Z. See review if article not available.
arXiv:0910.2349 Non-liftable Calabi-Yau spaces from arXiv Front: math.AG by Slawomir Cynk, Matthias Schuett We construct many new non-liftable three-dimensional Calabi-Yau spaces in positive characteristic. The technique relies on lifting a nodal model to a smooth rigid Calabi-Yau space over some number field as introduced by the first author and D. van Straten.
arXiv:0910.2589 Explicit Kummer surface theory for arbitrary characteristic from arXiv Front: math.AG by Jan Steffen Müller We explicitly find an equation and a projective embedding of the Kummer surface associated to the Jacobian of a curve of genus 2 given by an equation of the form y^2 + h(x)y = f(x) over an arbitrary ground field as well as several maps that can be used to perform arithmetic on it. This extends earlier work by Flynn and has applications, for instance, in computations of canonical heights for genus 2 Jacobians and in cryptography.
arXiv:0907.0298 Elliptic Surfaces from arXiv Front: math.NT by Matthias Schuett, Tetsuji Shioda This survey paper concerns elliptic surfaces with section. We give a detailed overview of the theory including many examples. Emphasis is placed on rational elliptic surfaces and elliptic K3 surfaces. To this end, we particularly review the theory of Mordell-Weil lattices and address arithmetic questions.
arXiv:1002.2142 A Lefschetz fixed point formula for singular arithmetic schemes with smooth generic fibres from arXiv Front: math.AG by Shun Tang In this article, we consider singular equivariant arithmetic schemes whose generic fibres are smooth. For such schemes, we prove a relative fixed point formula of Lefschetz type in the context of Arakelov geometry. This formula is an analog, in the arithmetic case, of the Lefschetz formula proved by R. W. Thomason. In particular, our result implies a fixed point formula which was conjectured by V. Maillot and D. Rössler.
arXiv:1003.2451 The Langlands-Kottwitz approach for some simple Shimura Varieties from arXiv Front: math.AG by Peter Scholze We show how the Langlands-Kottwitz method can be used to determine the semisimple local factors of the Hasse-Weil zeta-function of certain Shimura varieties. On the way, we prove a conjecture of Haines and Kottwitz in this special case.
http://mathoverflow.net/questions/40486/comparing-cohomology-over-mathbb-c-and-over-mathbb-f-q
<]]>- Arithmetic surfacesWrite comment View comments
arXiv:0911.0590 An explicit approach to residues on and dualizing sheaves of arithmetic surfaces from arXiv Front: math.AG by Matthew Morrow We develop a theory of residues for arithmetic surfaces, establish the reciprocity law around a point, and use the residue maps to explicitly construct the dualizing sheaf of the surface. These are generalisations of known results for surfaces over a perfect field. In an appendix, explicit local ramification theory is used to recover the fact that in the case of a local complete intersection the dualizing and canonical sheaves coincide.
arXiv:0911.2951 Zariski decompositions on arithmetic surfaces from arXiv Front: math.AG by Atsushi Moriwaki In this paper, we establish the Zariski decompositions of arithmetic R-divisors of continuous type on arithmetic surfaces and investigate several properties. We also develop the general theory of arithmetic R-divisors on arithmetic varieties.
arXiv:1101.1883 Grothendieck's trace map for arithmetic surfaces via residues and higher adeles from arXiv Front: math.AG by Matthew Morrow We establish the reciprocity law along a vertical curve for residues of differential forms on arithmetic surfaces, and describe Grothendieck's trace map of the surface as a sum of residues.
http://mathoverflow.net/questions/70942/minimal-model-of-a-surface-over-spec-mathbbz
<]]>- Arithmetic topologyWrite comment View comments
Primes-knots dictionary, see Morin thesis.
http://www.neverendingbooks.org/index.php/what-is-the-knot-associated-to-a-prime.html
http://mathoverflow.net/questions/50879/what-is-the-knot-associated-to-a-prime
http://www.neverendingbooks.org/index.php/who-dreamed-up-the-primesknots-analogy.html
http://mathoverflow.net/questions/4075/questions-about-analogy-between-spec-z-and-3-manifolds
http://mathoverflow.net/questions/31250/prime-numbers-as-knots-alexander-polynomial
There is a CONM volume on primes and knots.
arXiv:1204.4892 On the Iwasawa invariants of a link in the 3-sphere from arXiv Front: math.NT by Teruhisa Kadokami, Yasushi Mizusawa Based on the analogy between knots and primes, J. Hillman, D. Matei and M. Morishita defined the Iwasawa invariants for sequences of cyclic covers of links with an analogue of Iwasawa's class number formula of number fields. In this paper, we consider the existence of covers of links with prescribed Iwasawa invariants, discussing analogies in number theory. We also propose and consider a problem analogous to Greenberg's conjecture.
<]]>- ArtinWrite comment View comments
MathSciNet for Michael Artin
Emil Artin Collected Papers, 1 vol.
Exposition by Emil Artin, a selection. 1 vol.
<]]>- Artin approximationWrite comment View comments
Popescu chapter in Handbook of Algebra
References in my etale essay.
<]]>- Artin conjectureWrite comment View comments
http://mathoverflow.net/questions/11450/applications-of-artins-holomorphy-conjecture
arXiv:0912.0058 Artin's Conjecture and Elliptic Curves from arXiv Front: math.NT by Edray Herber Goins Artin conjectured that certain Galois representations should give rise to entire L-series. We give some history on the conjecture and motivation of why it should be true by discussing the one-dimensional case. The first known example to verify the conjecture in the icosahedral case did not surface until Buhler's work in 1977. We explain how this icosahedral representation is attached to a modular elliptic curve isogenous to its Galois conjugates, and then explain how it is associated to a cusp form of weight 5 with level prime to 5.
<]]>- Artin stackWrite comment View comments
For the Grothendieck ring of higher Artin stacks, see Toen: Anneaux de Grothendieck etc, file Toen web prepr K-champ.pdf. For special Artin stacks, he shows by comparing this ring to the ordinary Grothendieck ring of varieties, that invariants such as Hodge numbers and Euler characteristics (l-adic and motivic) extend uniquely to special Artin stacks. In particular, get Lefschetz trace formula for such stacks.
<]]>- AtiyahWrite comment View comments
Collected works, 6 vols
Wikipedia with quite a lot of material, including descriptions of the collected works
<]]>- Atiyah-Hirzebruch spectral sequenceWrite comment View comments
Lurie stable homotopy notes: p 1 describes AHSS for a multiplicative cohomology theory. Def of complex-orientable theory in terms of degeneration of AHSS at the second page. I think the intro of the Levine-Morel book mentions AHSS to algebraic cobordism. What should the general picture be for AHSS in algebraic geometry?
http://mathoverflow.net/questions/30788/torsion-in-k-theory-versus-torsion-in-cohomology
http://mathoverflow.net/questions/30917/relation-between-motivic-cohomology-and-quillen-k-theory
<]]>- Atiyah-Singer index theoremWrite comment View comments
http://mathoverflow.net/questions/1162/atiyah-singer-index-theorem
http://mathoverflow.net/questions/23409/intuitive-explanation-for-the-atiyah-singer-index-theorem
http://mathoverflow.net/questions/38007/index-of-an-operator
Several other MO questions on A-S as well.
Fedosov: Deformation quantization and index theory, in folder Geometry-Various.
The Atiyah-Singer Theorem and Elementary Number Theory (Mathematics Lecture No. 3) fra Mathematics by: F. Hirzebruch, D Zagier
<]]>- Automorphic formsWrite comment View comments
Deitmar: Automorphic forms: http://www.springer.com/mathematics/book/978-1-4471-4434-2
Many introductions and surveys by Borel, I think.
LNM0054 Shimura short introduction
Book: Automorphic forms and applications. IAS/Park City Math. Ser. 12, AMS, 2007.
Various things on automorphic forms and representations in the Automorphic folder under N TH. Also Modular forms folder
LNM340 (Deligne et al) has some really good stuff, for example on modular curves viewed as stack, and on correspondence between adelic and classical points of view.
Harish-Chandra lectures in LNM0062
Jacquet-Langlands LNM0114
LNM0189 Weil: Dirichlet series and automorphic forms. Including some nice history.
LNM0210 Eichler: Projective varieties and modular forms. Studies RR with the Dedekind-Weber approach (which allows for singularities) rather than the Weil approach. Applications to varieties of Siegel and Hilbert modular forms, also def and brief intro to these kinds of forms.
LNM0216 Maass H. Siegel's modular forms and Dirichlet series
shimura: introd to the arithm th of autom forms
hida: mod forms and gal cohomology
Bailey, Knapp eds: Rep theory and automorphic forms (PSPUM 61), AMS, 1997
A week in Strasbourg on cohomologies and automorphic forms
<]]>- Automorphic L-functionsWrite comment View comments
- <]]>
- Automorphic representationsWrite comment View comments
- <]]>
- Automorphisms of schemesWrite comment View comments
Hanamura has several papers on birational automorphisms of varieties, some general, some more special examples. See MathSciNet.
<]]>- Axioms in alg geom tempWrite comment View comments
For the concept of absolute purity, see Thomason's Absolute cohomological purity, in Thomason folder. Could try to show that the six functors statement implies the statement in terms of cohomology groups. The paper also briefly lists where absolute purity is used (Gysin maps, cycle maps and more).
<]]>- Axioms in algebraic geometryWrite comment View comments
Introduction
In algebraic geometry, it is not completely clear what a cohomology theory really is, or rather, there are many different useful definitions of "cohomology theory". There are several issues here:
The domain category
Different kinds of cohomology theories are defined on different subcategories of the category of schemes. The most friendly such category is probably the category of smooth projective varieties over a nice field, for example a field admitting resolution of singularities. In algebraic topology, there are also several natural domain categories for cohomology (finite CW complexes, CW complexes, compactly generated topological spaces, ...) but the situation are still far simpler than in algebraic geometry.
The axioms
While in algebraic topology, there is essentially only one list of axioms (Eilenberg-Steenrod), in algebraic geometry there are many different lists of axioms in the literature. Examples include Weil cohomology axioms, Bloch-Ogus axioms, and Oriented cohomology axioms. These differ substantially, and each list gives rise to its own "universal" theory (which generates quite a lot of interesting mathematics.)
Remark: Jannsen discusses other variants to the Bloch-Ogus axioms, by Gillet and by Beilinson (see p 37-38).
Rigidity - see paper by Hornbostel.
Descent properties!!
Representability and stable homotopy theory
In algebraic geometry, every cohomology theory is represented by a spectrum, and vice versa, so one could define a cohomology theory to be something represented by an object in the stable homotopy category of spectra. In algebraic geometry, things are more complicated. There are many different stable homotopy categories, and it is not at all clear that every cohomology theory is represented by a spectrum.
References
Some notes by Joshua containing a very interesting axiomatization. See also this Inventiones article containing some results on pseudo pretheories, by Ostvaer and Rosenschon.
Some axioms of Voevodsky
Kth76 (1995): Voevodsky discusses algebraic Morava K-theory, and defines there a cohomology theory by four axioms: Exactness, Nisnevich descent, and two types of homotopy invariance.
Voevodsky: BK conjecture for Z mod 2 coeffs and algebraic Morava K-theories. File in Voevodsky folder. Discussion of BK conj and related conjectures. P 32: axioms for cohomology theories on simplicial schemes. Proof that existence of algebraic Morava K-theories satisfying certain properties would imply the BK conjecture.
Jannsen
There are some kind of axioms for generalized cohomology in Jannsen Motives vol article. See also the ref Ja3 in this article for some possibly different axioms.
Bivariant theories
Fulton and MacPherson: Categorical framework for the study of singular spaces. In Geometry-Various folder. This seems to be the original source for bivariant theories in general, with quite a lot of material.
Voevodsky pretheory
See Pretheory
Voevodsky letter axioms
In the letter to Beilinson, Voevodsky formulates axioms for a homology theory. He considers
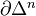as an (n-1)-dim sphere, write also S for the 1-dim sphere in this sense. Let Sch/k be the cat of separated schemes of finite type over a base k. Then a homological theory is a functor from Sch/k together with a family of natural isos 
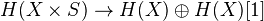. This functor should satisfy some conditions: Morally, homotopy invariance, MV exact triangle, an exact triangle for blowups, and transfer for flat finite morphisms. Get a 2-cat of homological theories over 
. Examples: Algebraic K-th with rational coeffs, l-adic homology, Hodge homology ass to a complex embedding. Thm: There is an initial object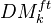 
in this cat, which we call the triang cat of eff mixed motives over k. Notion of reduced homological theory, and reduced motive of a scheme. Any motive in the above sense is of the form 
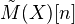, where we may assume affine and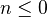 
. Tate object and comparison with K-theory. Bigger cat 
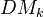which contains the previous as a full triang subcat, but admits a more explicit description rather than just the universal property. Can also be viewed as the closure of the previous, wrt direct sums and inductive limits. Need the h-topology, in particular coverings including surjective blowups, finite surjetive maps, etale coverings. Various filtrations on 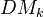(homotopy canonical, geometrical, motivic canonical, weight). The weight filtr should be related to pure numerical motives.References
In the first chapter of Levine-Morel, there is a nice discussion of axioms, and the relation between oriented theories and theories represented by spectra. Recommended: read the overview in the introduction, and the first two chapters. Another nice list is in Bloch's article on higher Chow groups.
In Levine, K-theory handbook, there is a description of "axiomatic" properties of the triangulated category of motives (which should be te derived category of Beilinson's abelian category of mixed motives). These axioms are: Additivity, Homotopy, Mayer-Vietoris, Kunneth, Gysin DT, Cycle classes, Unit, Motivic cohomology, and Projective bundle formula. See page 470.
In Levine there is also a notion of geometric cohomology theory. Should search the whole database for all notions of arithmetic and geometric CTs.
Should read Huber and Wildeshaus: Classical...
See MR1440308 for a many standard properties such as cohomological purity, excision, Gysin maps, finiteness, etc (for rigid cohomology).
Kahn, Coll-Th and Hoobler has a paper (Bloch-Ogus-Gabber theorem) where they discuss axioms in a rather nice way. This paper is removed from K-th archive and published in Fields Inst Comm.
Axioms related to motivic homotopy theory
There are some axiom sets in Déglise-Cisinski: Mixed Weil cohomology, and maybe also in Triang cats, in the stable homotopy theory section.
Various notions in a paper by Naumann? Spitzweck? et al?, maybe the paper on Landweber exactness. Graded, nongraded etc.
Thomason: Le principe de scindage (Thomason folder). He shows roughly that any theory for schemes satisfying certain axioms and mapping to Quillen K-theory, must be surjective when evaluated on the ground field
. This implies that Milnor K-theory, if required to satisfy these axioms, cannot be extended to the category of varieties over . The axioms are: should be a map from smooth quasi-projective k-varieties, to "multiplicative spectra", satisfing homotopy, Mayer-Vietoris, units axiom, and weak localization. See paper for details.There is something by Jannsen and Saito where they write down axioms for Borel-Moore homology I think.
arXiv:1208.2586 Invariants of upper motives from arXiv Front: math.KT by Olivier Haution Let H be a homology theory for algebraic varieties over a field k. To a complete k-variety X, one naturally associates an ideal of the coefficient ring H(k). We show that, when X is regular, this ideal depends only on the upper Chow motive of X. This generalises the classical results asserting that this ideal is a birational invariant of smooth varieties for particular choices of H, such as the Chow group. When H is the Grothendieck group of coherent sheaves, we obtain a lower bound on the canonical dimension of varieties. When H is the algebraic cobordism, we give a new proof of a theorem of Levine and Morel. Finally we discuss some splitting properties of geometrically unirational field extensions of small transcendence degree.
<]]>- Axioms in algebraic topologyWrite comment View comments
In algebraic topology, we "know" exactly what a cohomology theory is: it is a sequence of functors satisfying the Generalized Eilenberg-Steenrod axioms. This should be compared to the situation in algebraic geometry, where it is quite unclear what a cohomology theory really is.
<]]>- AyoubWrite comment View comments
- <]]>