Glossary

http://www.ncatlab.org/nlab/show/base+change

<]]>

Base change theoremsWrite comment View comments

Proper base change: For non-torsion sheaves, see Deninger article

Ayoub has general theorems which should specialize under realizations.

There should be some conceptual understanding of the duality between smooth and proper. Ask at MO maybe after reading SGA and Ayoub. This should explain the Hodge triangles of Deligne, and Tony's question.

There are some general ideas related to passing from characteristic zero to characteristic p, maybe via special fibers of something over a DVR. Some of this is hinted at here: http://mathoverflow.net/questions/90837/comparison-between-singular-and-etale-cohomology-in-batyrevs-paper-on-birational. This is related to base change, maybe, and should allow for comparison between Betti numbers of different kinds.

<]]>

BauesWrite comment View comments

Retired since April 2008. Could not find a personal web page, but some of his preprints are available here

<]]>

Baum-Connes conjectureWrite comment View comments

Relation to the Trace conjecture

Mislin-Valette: Book on the Baum-Connes conjecture. Valete: Intro to the Baum-Connes conj. Both in K-th folder.

<]]>

BeilinsonWrite comment View comments

http://mathoverflow.net/questions/54237/special-values-of-l-functions-as-periods

Wikipedia article

Publications:

Letter to Soulé, 1982
Height pairings between algebraic cycles
Higher regulators and values of L-functions (1984, in Russian)
Notes on absolute Hodge cohomology, 1986
Interpretation motivique de la conjecture de Zagier... (in Motives volumes, with Deligne)
Polylogarithms, 1992 (with Deligne)
Notes/note on motivic cohomology (with MacPherson and Schechtman, 1987)
Aomoto dilogarithms, mixed Hodge structures and motivic cohomology (with Goncharov et al, 1990)
Letter to Soulé, 11 Jan 1996
On the derived category of perverse sheaves
How to glue perverse sheaves
Faisceaux pervers (with Bernstein and Deligne)
Polylogarithm and cyclotomic elements (preprint)
Motivic polylogarithm and Zagier conjecture (preprint 1992, with Deligne)
Articles in Motive vol

<]]>

Beilinson conjecturesWrite comment View comments

http://mathoverflow.net/questions/36870/numerical-evidence-of-beilinsons-conjecture-in-local-fields-and-function-fields

http://mathoverflow.net/questions/22171/are-there-analogues-of-beilinsons-conjectures-for-motives-with-coefficients

<]]>

Beilinson conjectures BACKGROUNDWrite comment View comments

<]]>

Beilinson conjectures HEIGHT PAIRINGWrite comment View comments

Understand when the height pairing comes into the picture.

Schneider gives refs to three independent constructions of the height pairing: Beilinson, Bloch, and GS: Intersection sur les varieties d'Arakelov (C R Acad 299, 563-566 (1984) )

Beilinson's original article

Scholl: Height.dvi for "motivic reinterpretation"

<]]>

Beilinson conjectures KEY IDEASWrite comment View comments

What kind of geometric object do the conjectures talk about really? Even in the classical formulation, we always need to take motivic cohomology of an integral model. Scholbach's thesis, discussion of motives over Z in old and new sense. Why not just work with schemes over Z? (However, note that Scholbach can spread out a motive over Q)

Periods: Do we need to mention Kontsevich-Zagier???

Beilinson ideas on compatifying Z, various cohomology functors (maybe ass. to primes??), Arakelov motives, l.e.s. involving regulator.

Possibly mention arithmetic Chow groups, and the idea of covolume being the actual special value.

<]]>

Beilinson conjectures MOTIVES AND CT NOTIONSWrite comment View comments

Cover: - Pure - Ab. mixed - Triang. mixed - CTs: generalized/ordinary, geom/absolute. - Various constructions of motives, including realizations. - Explain first the dream, and then what is known. For example, explain why we cannot prove nice properties of pure motives, but we can define them. - Try to clarify whether we really need abelian mixed motives.

Scholl-Deninger section 2.9 explains how Deligne cohomology in a certain index range is isomorphic to a certain Ext^1 group in the cat of R-mixed Hodge structure with the action of a real Frobenius. (From this one would guess that Bette-Deligne is a geometric-absolute pair. Have working defs for MMQ and MMZ in terms of realizations, ref to Deligne: La groupe fondamental..., Scholl: Remarks on special values of L-functions, and LNM1400. For such motives get maps to Ext groups also for motivic cohomology, these are conjecturally isos. Some more details about this picture.

Expected dimension of cats of motives: This I believe is 1 (or 2??) for number fields, which maybe explains the form of the order of vanishing conjecture according to Kim, i.e. it's an "Euler char" but only 2 terms can possibly contribute.

Is it possible to say that a geometric-absolute pair is associated to every completion of a number field? Is this correct? The mystery is really de Rham-Betti-Deligne-absolute Hodge...

Relate the idea of oriented theories to Gillet's construction, for which the requirements are products, projective bundle thm, and weak Gysin.

Note: Motivic cohomology should be 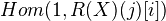Mathematical formula in the bounded derived cat of mixed motives, according to Jannsen. Here R is the functor from correspondences to the derived cat of mixed motives.

Jannsen end of p 285: Expectation that the cohomological dimension of mixed motives over a field is the Kronecker dimension of the field, so 1 in the global field case. and 0 for finite fields.

There is some discussion of the "integral part" of motivic cohomology in Bondarko's weights paper: http://front.math.ucdavis.edu/1007.4543

<]]>

Beilinson conjectures PROOF IDEASWrite comment View comments

Eisenstein symbol: See Deninger-Scholl section 4 and the imimediate stuff preceeding. This symbol is a certain "universal construction of elements of motivic cohomology of an elliptic curve, or a self-product of an elliptic curve. This looks really cool, there is some theorem by Beilinson about the regulator in this case. Some key concepts: Kuga-Sato var, a certain residue map from motivic cohomology, which is surjective by Beilinson's thm, the Eisenstein symbol being the inverse. Also L-functions of modular forms, and something about their associated motives, and stuff about critical points where everything is reduced to Deligne's conj, already proven in this case. More: L-functions of algebraic Hecke characters, giving results on Beilinson conj for certain Dirichlet characters and CM elliptic curves of Shimura type. Again rel to Deligne conj. Many references, comprehensive survey.

Somekawa on Fermat curves

What about polylogs??

Special cases survey, maybe in Nekovar?

Computer calculations? Dokchitser, de Jeu?

The work of Borel, explained in Burgos.

Poincaré duality over F1 or in some other sense???

<]]>

Beilinson conjectures QUESTIONSWrite comment View comments

Relation between zeta and L-functions, see Kim's notes. Partial answer (Kim): We don't have a good canonical def of the complete zeta function. Example for elliptic curve of partial zeta vs partial L-function. In this case, have recipe for bad factors, and also a canonical model, both give same answers. Agreement between etale cohomology of fiber of good model with inertia fixed points of of the thing / Q.

Can we ever hope to prove FE by some form of PD?? What is the analogue in the function field case?

Why not state the conjecture in terms of schemes over Z rather than varieties? We need to assume regular model anyway, right??

<]]>

Beilinson conjectures REFSWrite comment View comments

Beilinson: Higher regulators and values of L-functions.

Beilinson: Higher regulators of modular curves

Beilinson: Notes on absolute Hodge cohomology

Jannsen in the Motives volumes

http://londonnumbertheory.files.wordpress.com/2010/01/ihes1.pdf Kim slides on special values conjectures

http://mathoverflow.net/questions/2703/beilinson-conjectures maybe also other MO qs

The Hilbert-Polya strategy and height pairings by Deninger

A survey: Ramakrishnan: Regulators, algebraic cycles, and values of L-functions.

Rapoport, Schappacher, Schneider: book.

Nekovar in the Motives volume, for a motivic reformulation.

Concrete examples by de Jeu, Dokchitser, Zagier: Numerical verification of...

Other Motives vol articles?

Huber - on realizations, and maybe on the ideas of Beilinson??

Burgos book

Feliu thesis

arXiv:0909.3002 On the regulator of Fermat motives and generalized hypergeometric functions from arXiv Front: math.AG by Noriyuki Otsubo We calculate the Beilinson regulators of motives associated to Fermat curves and express them by special values of generalized hypergeometric functions. As a result, we obtain surjectivity results of the regulator, which support the Beilinson conjecture on special values of L-functions.

<]]>

Beilinson conjectures SPECIAL VALUES STATEMENTSWrite comment View comments

Scholl-Den start of section 3.

One can formulate a weaker conjecture by simply replacing the subscript Z motivic cohomology by an unspecified subspace.

Kim on p 13 says that the general conjecture about orders of vanishing is expressed in terms of a conjectural cat of mixed motives over Z, as dim Ext1 - dim Hom. Kim in general has a very nice structure on his overview, explaining what happens the central, near-central points etc, and explaining the rational and transcendental terms. He says the conceptual structure falls into two parts: Relations between and L-functions and Ext groups in cats of motives, and geometric interpretation of these Ext groups.

There is a formulation in Schneider.

<]]>

Beilinson conjectures TALKS OUTLINEWrite comment View comments

DAY 1:

Background on motives and cohomology
Statement of conjectures

DAY 2:

The regulator map: definitions and interpretations
The height pairing: definitions and interpretations
Evidence/proof ideas
Scholbach and F1 stuff somewhere

<]]>

Beilinson regulatorWrite comment View comments

S Saito and Asakura: Maximal components etc. review

Various defs of motivic cohomology: K-theory, analogous to Atiyah (see Atiyah: K-theory). Higher Chow groups. Voevodsky's complexes. Suslin-Friedlander??? Homotopical def.

Scholl and Deninger defines motivic cohomology with rational coeffs and Z subscript as the just the motivic cohomology for q>p, and as the image of motivic cohomology of a proper regular model. Conjecturally this is equiv to defining it in the latter way for all p,q.

Deligne cohomology should be interpreted as Exts in a cat of mixed Hodge structures (see Scholl-Den section 2.9)

Deligne cohomology relates to Betti and de Rham cohomology through a certain les, and also via 2 short exact sequence's. (Sch-Den p 3) so it seems like somehow we encode the period map, or some aspect of it, in the Deligne cohomology groups with Q-structure. For open varieties the naive def gives in general infinite-dimensional groups, must refine a little...

Bloch has a construction of the regulator, using higher Chow groups. This is briefly explained in Deninger-Scholl, section 2.8. Same construction works for continuous etale cohomology.

Abstract Chern class theory explained in Schneider. Relate this to oriented theories maybe.

Explain the regulator as a realization map.

The idea of defining the regulator on the level of complexes, or on the level of representing spectra.

Source: Nekovar, Feliu, ...

Various concrete cases of the regulator covered in the RSS volume

arXiv:1209.6451 Regulators and cycle maps in higher-dimensional differential algebraic K-theory fra arXiv Front: math.KT av Ulrich Bunke, Georg Tamme We develop differential algebraic K-theory of regular and separated schemes of finite type over Spec(Z). Our approach is based on a new construction of a functorial, spectrum level Beilinson regulator using differential forms. We construct a cycle map which represents differential algebraic K-theory classes by geometric vector bundles. As an application we derive Lott's relation between short exact sequences of geometric bundles with a higher analytic torsion form.

<]]>

Beilinson-Lichtenbaum conjecturesWrite comment View comments

See Levine in K-theory handbook, page 439-440. Statement: For 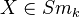Mathematical formula , existence of certain complexes in the derived category of sheaves on the Zariski (resp etale) site of , satisfying a list of properties.

<]]>

Beilinson-Soule vanishing conjectureWrite comment View comments

Reza Akhtar - Miami University Title: The Beilinson-Soulé vanishing conjecture with finite coefficients. Abstract: The Beilinson-Soulé vanishing conjecture asserts that for any variety $X$ over a field $k$, the motivic cohomology groups $H^i(X, \mathbb{Z}(n))$ vanish for $i<0$ and any $n$. We discuss a "finite coefficients" variation on this conjecture and give an elementary proof under the hypothesis that the base field contains an algebraically closed field.

<]]>

Beilinson-Tate conjectureWrite comment View comments

arXiv:0909.2670 Beilinson-Tate cycles on semiabelian varieties from arXiv Front: math.AG by Donu Arapura, Manish Kumar Along the lines of Hodge and Tate conjectures, Beilinson conjectured that in the qth cohomology all the weight 2q Hodge cycles of a smooth complex variety and all the weight 2q Tate cycles of a smooth variety over a finitely generated field comes from the higher Chow groups. For product of curves and semiabelian varieties, Beilinson-Hodge conjecture was shown in a previous paper by the authors. Here both Beilinson-Hodge and Beilinson-Tate conjectures are shown to be true for varieties dominated by product of curves. We also show that lower weight Hodge cycles (resp. Tate cycles) are algebraic in these situations.

<]]>

BerglundWrite comment View comments

<]]>

Bernoulli numbersWrite comment View comments

Baez problem sheet

Table of Bernoulli numbers in Washington

<]]>

BicategoryWrite comment View comments

Benabou intro in LNM0047

Leinster basics

<]]>

BiglariWrite comment View comments

IAS/PArk City proceedings from 2009

<]]>

Birational geometryWrite comment View comments

Folder Birational under AG

arXiv:1006.5156 Finite generation of adjoint rings after Lazic: an introduction from arXiv Front: math.AG by Alessio Corti An introduction to all the key ideas of Lazic's proof of the theorem on the finite generation of adjoint rings.

arXiv:1210.7382 Around and beyond the canonical class fra arXiv Front: math.AG av Vladimir Lazić This survey is an invitation to recent developments in higher dimensional birational geometry.

arXiv:1210.2670 Lectures on birational geometry fra arXiv Front: math.AG av Caucher Birkar Lecture notes of a course on birational geometry (taught at College de France, Winter 2011, with the support of Fondation Sciences Mathématiques de Paris). Topics covered: introduction into the subject, contractions and extremal rays, pairs and singularities, Kodaira dimension, minimal model program, cone and contraction, vanishing, base point freeness, flips and local finite generation, pl flips and extension theorems, existence of minimal models and Mori fibre spaces, global finite generation, etc.

<]]>

Birch-Swinnerton-Dyer conjectureWrite comment View comments

Clay formulation

A chapter in Husemoller: Elliptic curves

Brief notes in Silverberg: Open questions. In Elliptic curves folder

Stein: A computatinal approach. In Elliptic curves folder

http://mathoverflow.net/questions/11502/the-current-status-of-the-birch-swinnerton-dyer-conjecture

arXiv:0909.4803 On Neron class groups of abelian varieties from arXiv Front: math.NT by Cristian D. Gonzalez-Aviles Let F be a global field and let S denote a nonempty finite set of primes of F containing the set S' of archimedean primes of F. In this paper we study the Neron S-class group C{A,F,S} of an abelian variety A defined over F. In the well-known analogy that exists between the Birch and Swinnerton-Dyer conjecture for A over F and Dirichlet's analytic class number formula for the field F (in the number field case), the finite group C{A,F,S'} (not the Tate-Shafarevich group of A) is a natural analog of the ideal class group of F.

Summer school in Sardinia: See my own hand-written notes, or the typed-up notes when they appear, and Chris' own notes on his material.

Birch-Swinnerton-Dyer and parity (Vladimir Dokchitser). Topics: Review of the Birch-Swinnerton-Dyer conjecture and the parity conjecture, their consequences, isogeny invariance, finiteness of the Tate-Shafarevich group implies parity

L-functions and root numbers (Tim Dokchitser). Topics: Action of Galois on points of finite order and the Tate module, L-functions of elliptic curves, Artin formalism, root numbers and the functional equation.

Modular symbols and BSD over abelian fields (Christian Wuthrich). Topics: Modular symbols, Stickelberger elements, the Equivariant Tamagawa Number Conjecture for cyclic extensions, consequences for the Tate-Shafaravich.

<]]>

Bisimplicial setsWrite comment View comments

Jardine-Goerss chapter IV. Source of spectral sequence constructions, e.g. the Serre spectral sequence. There are many model structures, for example the Bousfield-Kan (pointwise WEs), the Reedy (pointwise WEs), the Moerdijk (diagonal WEs), and the E2 structures. Other spectral sequences include the Bousfield-Friedlander, which is in fact a reindexed version of the Bousfield-Kan spectral sequence for a tower of fibrations.

<]]>

Blakers-Massey theoremWrite comment View comments

<]]>

BlochWrite comment View comments

Young mathematicians network

Selected publications:

and algebraic cycles (1974)
Gersten's conjecture and the homology of schemes (1974, with Ogus)
Algebraic K-theory and crystalline cohomology (1977)
Algebraic K-theory and classfield theory for arithmetic surfaces (1981)
Height pairings for algebraic cycles (1984)
Higher regulators, algebraic K-theory and zeta functions of elliptic curves. Irvine lectures, (reprinted?) 2000.
Algebraic cycles and higher K-theory (1986)
A note on Gersten's conjecture in the mixed characteristic case (1986)
Algebraic cycles and the Beilinson conjectures (1986)
The moving lemma for higher Chow groups (1994)
L-functions and Tamagawa numbers of motives (with Kato, 1990)
Mixed Tate motives (with Kriz, 1994)
Deligne groups (unpublished)
Lectures on algebraic cycles
A spectral sequence for motivic cohomology (with Lichtenbaum, 1995)

<]]>

Bloch's conjectureWrite comment View comments

Claudio Pedrini, Bloch's conjecture and the $K$-theory of projective surfaces (195--213)

<]]>

Bloch-Kato conjectureWrite comment View comments

The best starting point might be Weibel's attempt to structure and survey the whole proof, and his list of references. See his webpage, or notes from some talk og his.

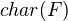Let Mathematical formula be a field, and an integer, prime to . Then the Galois symbol

The command "\\" may only appear inside a "\begin ... \end" block

\\theta: K^M_q(F) / n \\to H^p_{Gal}(F, \\mu_n^{\\otimes q})

is an isomorphism.

For background on many ideas, see Gille and Szamuely, in Various folder under ALGEBRA

Some related papers

Voevodsky-Suslin

Voevodsky and Suslin: Bloch-Kato conj and motivic cohomology with finite coeffs, file in Voevodsky folder

Voevodsky: BK conjecture for Z mod 2 coeffs and algebraic Morava K-theories. File in Voevodsky folder. Discussion of BK conj and related conjectures. P 32: axioms for cohomology theories on simplicial schemes. Proof that existence of algebraic Morava K-theories satisfying certain properties would imply the BK conjecture.

Weibel on some axioms related to the Voevodsky-Rost program: K0809

Some special case, by Koya, and another special case

Something by Levine and Geisser

An ingredient on norm varieties

The Gersten conjecture for Milnor K-theory , by Moritz Kerz

Papers involved in BK proof, from Weibel talk: Weibel , J Top 2009, pp346 V: Eilenberg-M spaces V: Motivic cohomology with Z/2 coeffs IHES 2003 V: Reduced power ops (not refereed/published) Suslin-Joukhovitsky JPAA 206. Haesemeyer-W: Chain lemma etc after Rost, Oslo Symposium 2009 Rost: Chain lemma etc, on his website V: Simplicial radditive functors, AKA Delta-closed classes V: Motives over simplicial schemes V: Motivic cohomology with Z/l coeffs (2003, 2008) S-V: Bloch-Kato paper 2001 Also Geisser-Levine Suslin: Grayson spectral sequence

<]]>

Bloch-Kato conjecture on L-valuesWrite comment View comments

To understand Bloch-Kato conj, read Fontaine 1991 Bourbaki talk in his folder.

<]]>

Bloch-Ogus-Gabber theoremWrite comment View comments

Kahn et al: The Bloch-Ogus-Gabber theorem

<]]>

BlogsWrite comment View comments

Rigorous trivialities

n-category cafe

Noncommutative geometry

Number theory research

Low-dimensional topology

Secret blogging seminar

Gowers, Tao, vivatsgasse

Not even wrong (Physics)

Kowalski

Mathematics and Physics (Borcherds)

Not really blogs

Slashdot

http://www.eurekajournalwatch.org/index.php/Main_Page

ResarchGate?

<]]>

BondalWrite comment View comments

Could not find a personal web page.

<]]>

BondarkoWrite comment View comments

http://mathoverflow.net/questions/53036/books-you-would-like-to-read-if-somebody-would-just-write-them

<]]>

BooksWrite comment View comments

<]]>

Boolean localisationWrite comment View comments

A trick that faithfully embeds any Grothendieck topos into one that satisfies the axiom of choice. ("Barr's theorem")

<]]>

BorelWrite comment View comments

Wikipedia page

Notices article on Borel\'s life

Borel Oeuvres/Collected papers, 4 vols

Selected publications:

Stable real cohomology of arithmetic groups (1974)
Cohomologie de 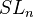et valeurs de fonctions zeta aux points entiers (1977). Errata (1980)
Values of zeta functions at integers, cohomology and polylogarithms (1995)
The rank conjecture for number fields (with Yang, 1994)

<]]>

Borel conjectureWrite comment View comments

Ref: Carlsson in K-theory handbook, page 30. Conjecture: Two homotopy equivalent closed 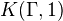Mathematical formula -manifolds are homeomorphic.

<]]>

Borel regulatorWrite comment View comments

943 : Computing Borel’s Regulator II, by Zacky Choo, Wajid Mannan, Rubén J. Sánchez-García, and Victor P. Snaith. In our earlier article we described a power series formula for the Borel regulator evaluated on the odd-dimensional homology of the general linear group of a number field and, concentrating on dimension three for simplicity, described a computer algorithm which calculates the value to any chosen degree of accuracy. In this sequel we give an algorithm for the construction of the input homology classes and describe the results of one cyclotomic field computation. Zacky Choo zackychoo@yahoo.com Wajid Mannan wajid@mannan.info Rubén J. Sánchez-García sanchez@math.uni-duesseldorf.de Victor P. Snaith V.Snaith@sheffield.ac.uk

First article by Choo et al is here: http://front.math.ucdavis.edu/0908.3765

<]]>

BorgerWrite comment View comments

Webpage of Borger

<]]>

BottWrite comment View comments

Collected papers, 4 vols

<]]>

BourbakiWrite comment View comments

Seminaire Bourbaki at NUMDAM.

Wikipedia entry

Bourbaki archives as pointed out by "Not even wrong"

<]]>

BousfieldWrite comment View comments

http://ncatlab.org/nlab/show/Bousfield+localization+of+triangulated+categories

Apparently no web page.

Only one paper on arXiv (as of March 2009), downloaded

<]]>

Bousfield localizationWrite comment View comments

The original source might be the best: Bousfield, A.K., Kan, D.M.: Homotopy Limits, Completions and Localizations. Lecture Notes in Mat. 304, Springer-Verlag, 1972

See slides of Strickland.

Chapter X of Goerss-Jardine.

Neisendorfer in Homotopy folder: Algebraic methods in unstable homotopy theory. Huge book, including among other things a presentation of localization theory, well worth reading!

A paper of Hovey

Bousfield: The localization of spectra with respect to homology. Topology 18 (1979), 257-281.

A good reference in probably the book of Hirschhorn

nLab

Vaquie in Seville lectures: On existence of left Bousfield loc for a combinatorial and left proper MC. "Cellular" statement is in Hirschhorn, but combinatorial is folklore.

<]]>

BPS stateWrite comment View comments

http://nlab.mathforge.org/nlab/show/BPS-state

<]]>

Braided tensor categoryWrite comment View comments

Joyal and Street: Braided tensor categories. Adv Math 102.

<]]>

BraneWrite comment View comments

http://nlab.mathforge.org/nlab/show/brane

<]]>

BrauerWrite comment View comments

See article on his life and work.

There are Collected Papers, 3 volumes

<]]>

Brauer groupWrite comment View comments

LNM0181 DeMeyer and Ingraham

http://math.columbia.edu/~dejong/wordpress/?p=2062

Skorobogatov: torsors book, for good intro to selmer/brauer gps etc.

Check work of Skorobogatov and Colliot-Th.

File: Brauer group basics, in folder AG/Various

Skorobogatov webpage

Skorobogatov and Zarhin: A finiteness thm for the Brauer group of abelian varieties and K3 surfaces

http://mathoverflow.net/questions/67812/is-the-brauer-group-of-a-surface-an-elliptic-curve

http://mathoverflow.net/questions/7537/two-conjectures-by-gabber-on-brauer-and-picard-groups

http://mathoverflow.net/questions/78508/brauer-group-of-complete-dvr

http://mathoverflow.net/questions/79575/how-do-brauer-groups-relate-to-zeta-functions

A book by Caenepeel with material on Grothendieck topologies and Br.

See the end of Jinhyun Park's note on proper base change, last paragraph on representability of Pic. Is there a Brauer scheme representing Br???

arXiv:1211.6161 Etale twists in noncommutative algebraic geometry and the twisted Brauer space fra arXiv Front: math.AG av Benjamin Antieau This paper studies etale twists of derived categories of schemes and associative algebras. A general method, based on a new construction called the twisted Brauer space, is given for classifying etale twists, and a complete classification is carried out for genus 0 curves, quadrics, and noncommutative projective spaces. A partial classification is given for curves of higher genus. The techniques build upon my recent work with David Gepner on the Brauer groups of commutative ring spectra.

arXiv:1210.0290 Brauer groups and étale cohomology in derived algebraic geometry fra arXiv Front: math.AG av Benjamin Antieau, David Gepner In this paper, we study Azumaya algebras and Brauer groups in derived algebraic geometry. We establish various fundamental facts about Brauer groups in this setting, and we provide a computational tool, which we use to compute the Brauer group in several examples. In particular, we show that the Brauer group of the sphere spectrum vanishes, and we use this to prove two uniqueness theorems for the stable homotopy category. Our key technical results include the local geometricity, in the sense of Artin n-stacks, of the moduli space of perfect modules over a smooth and proper algebra, the étale local triviality of Azumaya algebras over connective derived schemes, and a local to global principle for the algebraicity of stacks of stable categories.

Alexei Skorobogatov (Imperial). Talk from 2012? "Towards calculating the transcendental Brauer group" (MR13, 2:30pm as usual) Abstract: The transcendental Brauer group is the part of the Brauer group of a variety that survives the extension of the ground field to its algebraic closure. I will address the finiteness problem for the transcendental Brauer group, give examples when it can be bounded or even computed explicitly, and discuss some other related results.

<]]>

Brauer inductionWrite comment View comments

Snaith has many papers on explicit Brauer induction.

<]]>

Brave new algebraWrite comment View comments

Here is a short introduction, and an even better one

A survey by May

Papers by May

An introductory article of Greenlees

An interesting article on different approaches to the "smash product problem": K0319; see also K0320 for the corresponding model structures.

http://mathoverflow.net/questions/4561/what-is-the-intuition-behind-brave-new-algebra

<]]>

Brave new algebraic geometryWrite comment View comments

Toen and Vezzosi, file Toen web publ del.pdf

Toen and Vaquie: Under Spec Z. Some notes: Idea: Relative alg geom. Think of commutative monoids in a symm monoidal cat C as models for affine schemes relative to C. If there is a reasonable symmetric monoidal functor from C to Z-modules, get a base change functor, and a notion of scheme under Spec(Z). Homotopical version of this requires C to have a model structure. Now have flat and Zariski topology. Can make sense of schemes: a functor with a Zariski covering. Stuff about toric varieties and GL. Brave new AG over the sphere spectrum, and the spectrum with one element. For the sphere spectrum, we start with the symmetric monoidal model cat of Gamma-spaces (very special??), whose homotopy cat is equivalent to the homotopy cat of connective symmetric spectra. The corresponding model cat of commutative monoids is a model for the homotopy theory of brave new comm rings. For the spectrum with one element, we start with C being simplicial sets.

<]]>

BreenWrite comment View comments

<]]>

BridgelandWrite comment View comments

This wonderful man is putting all his papers on his webpage.

<]]>

Brieskorn modulesWrite comment View comments

MR2351618 Barlet and Saito: Brieskorn modules and Gauss-Manin systems for non-isolated hypersurface singularities

<]]>

BrownWrite comment View comments

There are several Browns.

Some publications

R. Brown: Convenient categories of topological spaces: historical note. Preprint.

Ronald Brown

Webpage

Kenneth S. Brown (Ken Brown)

About the paper: Abstract homotopy theory and generalized sheaf cohomology: nLab

Edgar Brown

http://mathoverflow.net/questions/71812/on-brown-representability-theorem

<]]>

Brown representabilityWrite comment View comments

For the classical theorem in topology, see Classical Brown representability. For an abstraction of this, see Abstract Brown representability

LNM0012: Halbexakte Homotopiefunktoren, studies systematically the functors satisfying the conditions for Brown rep. Unfortunately in German...

http://mathoverflow.net/questions/11458/applications-of-the-brown-representability-theorem

Jardine preprint June 2009.

See Motivic homotopy theory for a summary of Voevodsky's ICM talk.

Joyal and Tierney: Classifying spaces for sheaves of simplicial groupoids. MR1239557 Has a rep result for H1 in the sense of iso classes of G-torsors, in a cat of simplicial sheaves.

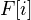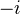One can express sheaf cohomology as Hom in the bounded derived category of abelian sheaves on Mathematical formula , from the constant sheaf Z to the sheaf which is placed in degree I think.

A survey of well generated triangulated categories. (English summary) Representations of algebras and related topics, 307--329, Fields Inst. Commun., 45. Summarizes Neeman\'s book on triang cats. I don\'t have this book I think

http://ncatlab.org/nlab/show/Brown+representability+theorem

http://mathoverflow.net/questions/32287/representing-cohomology-of-a-sheaf-a-la-eilenberg-maclane

http://ncatlab.org/nlab/show/representable+functor

http://www.ncatlab.org/nlab/show/Eilenberg-MacLane+object

Naumann in talk July 2009: SH(Z) is Brown, meaning that there is a Brown rep thm I think.

arXiv:0909.1943 Brown representability in $\A^1$-homotopy theory from arXiv Front: math.AG by N. Naumann, M. Spitzweck We prove the following result of V. Voevodsky. If $S$ is a finite dimensional noetherian scheme such that $S=\cup\alpha\Spec(R\alpha)$ for {\em countable} rings $R_\alpha$, then the stable motivic homotopy category over $S$ satisfies Brown representability.

Email from Oriol Raventos Feb 2010:

Hi Andreas,

I'm actually writing my PhD on this. It's not finished yet, but I'm also writing a small preprint, since some other people asked me about it. I'll send it to you as soon as I have it.

In the meanwhile, you can look at the slides of the talk of Fernando Muro in a recent conference in Prague:

http://personal.us.es/fmuro/talks.htm

I can provide you any details if you need them.

We haven't looked carefully at the case of Motivic Homotopy Theory, although we thought the paper in the Arxiv by Nauman and Spitzweck about it could be very interesting.

I hope it helped. If you have some more concrete question I'll may try to answer it. Anyway I'll send you the first draft when I have it.

Best wishes,

Oriol Raventós

<]]>

Brown-Gersten spectral sequenceWrite comment View comments

arXiv:0912.3786 Cech approximation to the Brown-Gersten spectral sequence from arXiv Front: math.KT by Benjamin Antieau In this paper, we show that the etale index of a torsion cohomological Brauer class is divisible by the period of the class. The tool used to make this computation is the Cech approximation of the title. To create the approximation, we use the folklore theorem that the homotopy limit and Postnikov spectral sequences for a cosimplicial space agree beginning with the E2-page. As far we know, this folklore theorem has no proof in the literature, so we include a proof.

<]]>

BundleWrite comment View comments

http://www.ncatlab.org/nlab/show/bundle

Bundles for adults: http://chromotopy.org/?p=25

<]]>

Burgos GilWrite comment View comments

Note: Sometimes referred as just Burgos, or maybe even just Gil.

Webpage. Includes publication list with links to MathSciNet and some articles as pdf files.