Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- C-star algebraWrite comment View comments
http://nlab.mathforge.org/nlab/show/C-star+algebra
arXiv:1004.1488 The unitary symmetric monoidal model category of small C-categories from arXiv Front: math.CT by Ivo Dell'Ambrogio 1 person liked this We produce a cofibrantly generated simplicial symmetric monoidal model structure for the category of (small unital) C-categories, whose weak equivalences are the unitary equivalences. The closed monoidal structure consists of the maximal tensor product, which generalizes that of C-algebras, with the Ghez-Lima-Roberts C-categories of -functors, C(A,B), providing the internal Hom's.
C*-algebras: See many things in the folder Noncomm geom and Cstar-alg.
<]]>- Calabi-Yau varietyWrite comment View comments
The last chapters of Husemoller contains intro to Calabi-Yau and K3 stuff
<]]>- Calculus of functorsWrite comment View comments
http://mathoverflow.net/questions/38911/a-reference-for-calculus-of-functors-for-model-categories
arXiv:1208.1919 On calculus of functors in model categories from arXiv Front: math.CT by Alexandru E. Stanculescu We present an analysis of some constructions and arguments from the universe of T. G. Goodwillie's Calculus, in a general model theoretic setting.
<]]>- CartanWrite comment View comments
Elie Cartan, Oeuvres completes, 3 vols
H Cartan, collected works, 3 vols
<]]>- CartierWrite comment View comments
- <]]>
- Cartier dualityWrite comment View comments
- <]]>
- Categorical sheavesWrite comment View comments
- <]]>
- CategorificationWrite comment View comments
nLab on horizontal categorification. Example: L-infinity algebras, I think.
http://mathoverflow.net/questions/4841/what-precisely-is-categorification
See also n-Lab on categorification
arXiv:1011.0144 Lectures on algebraic categorification from arXiv Front: math.CT by Volodymyr Mazorchuk This is a write-up of the lectures given by the author during the Master Class "Categorification" at Århus University, Denmark in October 2010.
Email from Alexander Palen Ellis: My advisor's (and by extension, I guess, my) main project right now is categorification of representations. The basic idea given an algebra A, we want to find a category and some distinguished endo-functors acting on something, such that when you take K0 of the whole mess you recover your original algebra A acting on various modules for that algebra. The case we care about most is when A is a quantum group, say Uq(g) -- if this can be successfully done, then the Hopf algebra structure on Uq(g) lifts to a "Hopf category" structure on the categorification. This in turn, by work of Frenkel, should yield interesting 4D TQFTS (there are already 3D ones from Uq(g) itself). More generally, one expects categorification to "jack up the dimension" of existing invariants of things, yielding much richer structures. In particular, you often get integrality / positivity results (since you can interpret certain structure constants in an algebra as "the number of times you've applied a certain functor").
For categorification of the character of a linear rep, see Toen preprint: infty-categories monoidales rigides etc. File Toen web prepr dag-loop.pdf.
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Contains quite a lot of material of categorification.
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Notion of derived cat sheaves, a categorification of the notion of complexes of sheaves of O-modules on schemes (also quasi-cohomology and perfect versions). Chern character for these categorical sheaves, a categorified version of the Chern char for perfect complexes with values in cyclic homology. Idea of categorical sheaves: For X a scheme, should have a symmetric monoidal 2-cat Cat(X) which is a categorification of Mod(X), in the sense that Mod(X) should be the cat of endomorphisms of the unit objects in Cat(X). More details. Categorification of homological algebra and dg-cats. See Derived categorical sheaves for a longer summary of this paper.
"One common feature of recent trends is “categorification”, often synonymous with “geometrization”. Categorification stands for the passage from a traditional mathematical object to its higher categorical analogue, and, more loosely, for the emphasis on categories instead of particular objects. The categories involved are typically of geometric nature (categories of sheaves of certain kind) and are constructed in a homological framework, i.e., they are triangulated categories, or refinements of these. Examples in representation theory include geometric Langlands duality, ..., homological mirror symmetry and, more generally, focus on derived categories of coherent sheaves in algebraic geometry, which is a categorification of standard cohomology theories."
<]]>- Category theoryWrite comment View comments
See Category folder under Foundations
http://www.ncatlab.org/nlab/show/database+of+categories
http://nlab.mathforge.org/nlab/show/stuff%2C+structure%2C+property
Borceaux volumes
Joyal's list of majojr currents in category theory, email to categories list in Dec 2009:
1) Algebraic topology and homological algebra 2) Abelian categories 3) Algebraic geometry and topos theory 4) General cartesian algebra 5) Categorical logic 6) Homotopical algebra 7) Elementary topos theory and set theory 8) Monoidal categories and enriched category theory 9) General tensor algebra and coalgebra 10) Category theory and computer science 11) Quantum field theory 12) Higher categories and homotopy theory
Algebraic theories and limit sketches are included in (4). Multicategories, operads are included in (9).
I have included Quillen homotopical algebra in (6).
<]]>- Category theory conceptsWrite comment View comments
Annoying precision has many really nice posts on basic category theory. Including, I think, the Yoneda lemma, epis and monos, and the center of a group.
http://www.ncatlab.org/nlab/show/closed+monoidal+category related to cartesian closed category
http://mathoverflow.net/questions/57099/why-do-filtered-colimits-commute-with-finite-limits
http://mathoverflow.net/questions/78471/intuition-for-coends
http://mathoverflow.net/questions/83437/the-main-theorems-of-category-theory-and-their-applications
http://mathoverflow.net/questions/32071/is-the-dual-notion-of-a-presheaf-useful
<]]>- Category theory readingWrite comment View comments
For spaces and spectra over a category, see Davis and Lueck
A bibliography from Stanford Encyclopedia of Philosophy
<]]>- Cellular varietiesWrite comment View comments
http://mathoverflow.net/questions/76480/an-example-of-an-affine-variety-with-non-zero-chow-groups contains some comment about quadrics
<]]>- Central simple algebrasWrite comment View comments
A good reference book for the material underlying the work of Rost, Voevodsky, Suslin, Merkurjev and others in this direction.
<]]>- Characteristic classesWrite comment View comments
References: Hatcher. Milnor and Stasheff (1974)
For one approach (through sheaf cohomology maybe), see Iversen, in Homol alg folder
http://mathoverflow.net/questions/9676/characteristic-classes-in-generalized-cohomology-theories nice remark by Tilson
<]]>- Cheeger-Simons classesWrite comment View comments
For CS secondary char classes, see maybe MR1472547
<]]>- ChernWrite comment View comments
Selected papers, 4 vols. Also book: Chern a great geometer etc
<]]>- Chern characterWrite comment View comments
A very general notion of Chern character is found in Toen preprint: infty-categories monoidales rigides etc. File Toen web prepr dag-loop.pdf. See also Derived categorical sheaves
http://mathoverflow.net/questions/60403/can-chern-class-character-be-categorified
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Notion of derived cat sheaves, a categorification of the notion of complexes of sheaves of O-modules on schemes (also quasi-cohomology and perfect versions). Chern character for these categorical sheaves, a categorified version of the Chern char for perfect complexes with values in cyclic homology. Using the derived loop space. "This work can be seen as an attempt to define algebraic analogues of of elliptic objects and char classes for them". 1. Motivations: Elliptic cohomology, geometric interpretations, chromatic level and n-categorical level, 2-VBs. Maybe the typical generalized CT of chromatic level n should be related to n-cats, more precisely cohomology classes should be rep by maps from X to a certain n-stack. Rognes red-shift conjecture: Intuitively saying that the K-th spectrum of a commutative ring spectrum of chrom level n is of chrom level (n+1). More on ell cohomology and 2-cats. Idea of categorical sheaves: For X a scheme, should have a symmetric monoidal 2-cat Cat(X) which is a categorification of Mod(X), in the sense that Mod(X) should be the cat of endomorphisms of the unit objects in Cat(X). More details. Notions of secondary cohomology and secondary K-theory. Notion of derived categorical sheaves, more reasonable than nonderived version. Relation between
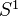 -equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.<]]>
-equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.<]]>- Chern classesWrite comment View comments
Grothendieck: La théorie des classes de Chern
See also Hatcher\'s book on K-theory and vector bundles
Chern classes and RR formalism at Concrete Nonsense
Scheider in the RSS volume has a very nice expose of Gillet's general construction of Chern classes. In the Beilinson conj survey, pp11.
<]]>- Chern-Simons theoryWrite comment View comments
- <]]>
- ChowWrite comment View comments
Collected papers 1 vol, ed Chern and Shokurov
<]]>- Chow-Kunneth decompositionWrite comment View comments
Several articles by Murre, see for example his survey in "Transcendental aspects of algebraic cycles". Some of them in Reine, not in Murre folder.
<]]>- Chromatic motivic homotopy theoryWrite comment View comments
arXiv:1002.5007 Motivic invariants of p-adic fields from arXiv Front: math.KT by Kyle M. Ormsby I provide a complete analysis of the motivic Adams spectral sequences converging to the bigraded coefficients of the 2-completions of the motivic spectra BPGL and kgl over p-adic fields, p>2. The former spectrum is the algebraic Brown-Peterson spectrum at the prime 2 (and hence is part of the study of algebraic cobordism), and the latter is a certain BPGL-module that plays the role of a "connective" motivic algebraic K-theory spectrum. This is the first in a series of two papers investigating motivic invariants of p-adic fields, and it lays the groundwork for an understanding of the motivic Adams-Novikov spectral sequence over such base fields.
<]]>- Chromatic pictureWrite comment View comments
Kuhn: Goodwillie towers and chromatic homotopy: an overview
Possible "way in": http://chromotopy.org/?p=372
http://mathoverflow.net/questions/87174/absence-of-maps-between-p-local-and-q-local-spectra
Some slides of Ravenel
Talbot 2013 workshop on chromatic homotopy theory.
More slides of Ravenel
Here is something about uniqueness of triangulated cats.
Chromotopy write a lot about chromatic homotopy...
http://sbseminar.wordpress.com/2010/01/28/chromatic-stable-homotopy-theory-and-the-ahss
arXiv:0911.5238 Continuous homotopy fixed points for Lubin-Tate spectra from arXiv Front: math.AT by Gereon Quick We construct a stable model structure on profinite symmetric spectra with a continuous action of an arbitrary profinite group. This provides a natural framework for a new construction of homotopy fixed point spectra and of homotopy fixed point spectral sequences for the action of the extended Morava stabilizer group on Lubin-Tate spectra. These continuous homotopy fixed points are canonically equivalent to the homotopy fixed points of Devinatz and Hopkins but have a drastically simplified construction.
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Notion of derived cat sheaves, a categorification of the notion of complexes of sheaves of O-modules on schemes (also quasi-cohomology and perfect versions). Chern character for these categorical sheaves, a categorified version of the Chern char for perfect complexes with values in cyclic homology. Using the derived loop space. "This work can be seen as an attempt to define algebraic analogues of of elliptic objects and char classes for them". 1. Motivations: Elliptic cohomology, geometric interpretations, chromatic level and n-categorical level, 2-VBs. Maybe the typical generalized CT of chromatic level n should be related to n-cats, more precisely cohomology classes should be rep by maps from X to a certain n-stack. Rognes red-shift conjecture: Intuitively saying that the K-th spectrum of a commutative ring spectrum of chrom level n is of chrom level (n+1). More on ell cohomology and 2-cats. Idea of categorical sheaves: For X a scheme, should have a symmetric monoidal 2-cat Cat(X) which is a categorification of Mod(X), in the sense that Mod(X) should be the cat of endomorphisms of the unit objects in Cat(X). More details. Notions of secondary cohomology and secondary K-theory. Notion of derived categorical sheaves, more reasonable than nonderived version. Relation between
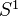 -equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.
-equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.arXiv:1101.5201 Every K(n)-local spectrum is the homotopy fixed points of its Morava module from arXiv Front: math.AT by Daniel G. Davis, Takeshi Torii Let n \geq 1 and let p be any prime. Also, let En be the Lubin-Tate spectrum, Gn the extended Morava stabilizer group, and K(n) the nth Morava K-theory spectrum. Then work of Devinatz and Hopkins and some results due to Behrens and the first author of this note, show that if X is a finite spectrum, then the localization L{K(n)}(X) is equivalent to the homotopy fixed point spectrum (L{K(n)}(En \wedge X))^{hGn}, which is formed with respect to the continuous action of Gn on L{K(n)}(En \wedge X). In this note, we show that this equivalence holds for any (S-cofibrant) spectrum X. Also, we show that for all such X, the strongly convergent Adams-type spectral sequence abutting to \pi\ast(L{K(n)}(X)) is isomorphic to the descent spectral sequence that abuts to \pi\ast((L{K(n)}(En \wedge X))^{hG_n}).
<]]>- CisinskiWrite comment View comments
- <]]>
- Class field theoryWrite comment View comments
Bourbaki exp 42: Local CFT following Hochschild
Exp 47: Nonabelian generalisation of local CFT
Exp 83: Weil on class field theory
Class field theory folder
Cox: Primes of the form etc, is an excellent book
http://londonnumbertheory.wordpress.com/2009/10/07/questions-on-class-field-theory/ mentions among other things an analogy between generalized Jacobians and what I think is ray class groups wrt some modulus.
http://londonnumbertheory.wordpress.com/2009/10/15/computational-class-field-theory/
Ulrich Thiel: Mackey functors and abelian class field theories. Abstract: Motivated by the work of Jürgen Neukirch and Ivan Fesenko we propose a general definition of an abelian class field theory from a purely group-theoretical and functorial point of view. This definition allows a modeling of abelian extensions of a field inside more general objects than the invariants of a discrete module over the absolute Galois group of the field. The main objects serving as such models are cohomological Mackey functors as they have enough structure to make several reduction theorems of classical approaches work in this generalized setting and, as observed by Fesenko, they even have enough structure to make Neukirch's approach to class field theories via Frobenius lifts work. This approach is discussed in full detail and in its most general setting, including the pro-P setting proposed by Neukirch. As an application and justification of this generalization we describe Fesenko's approach to class field theory of higher local fields of positive characteristic, where the modeling of abelian extensions takes place inside the cohomological Mackey functor formed by the Milnor-Paršin K-groups. The motivation for this work (which is the author's Diplom thesis) was the attempt to understand what a class field theory is and to give a single-line definition which captures certain common aspects of several instances of class field theories. We do not claim to prove any new theorem here, but we think that our general and uniform approach offers a point of view not discussed in this form in the existing literature.
<]]>- Classical Brown representabilityWrite comment View comments
http://golem.ph.utexas.edu/category/2012/08/brown_representability.html
http://mathoverflow.net/questions/104866/brown-representability-for-non-connected-spaces
http://mathoverflow.net/questions/1346/representablity-of-cohomology-ring
http://mathoverflow.net/questions/1438/why-is-homology-not-corepresentable
We follow Kono and Tamaki.
We say that a functor
 is a homotopy functor if
is a homotopy functor if 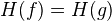 whenever
whenever  is homotopic to
is homotopic to 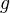 . I guess this is the same as a functor on the homotopy category.
. I guess this is the same as a functor on the homotopy category.A contravariant representable homotopy functor must satisfy the Wedge axiom and a Mayer-Vietoris property: For two subspaces
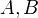 of a space
of a space  , and two elements
, and two elements 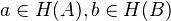 , there exists an element
, there exists an element 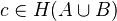 which "restricts" to
which "restricts" to 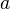 and to
and to 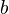 .
.A homotopy functor satisfying these two properties is called a Brown functor. (We also require
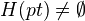 )
)Thm: A Brown functor takes values in
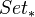 . Moreover,
. Moreover, 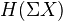 is a group and
is a group and 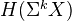 is an abelian group for
is an abelian group for 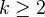 .
.Thm: Any Brown functor is representable. Similar statement for finite CW complexes, under some additional hypothesis.
<]]>- Classifying spaceWrite comment View comments
[nLab on Classifying topos and Classifying space
Jardine-Goerss chapter V treats simplicial sets with an action of a simplicial group, classification of principal
 -fibrations, construction of a model of
-fibrations, construction of a model of 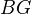 via universal cocycles.
via universal cocycles. There are descriptions of the mod p cohomology of the classifying spaces of compact Lie groups, see LNM1370, and Dwyer, Wilkerson: A cohomology decomposition thm (1992).
Dwyer et al: Homotopical uniqueness of classifying spaces
Book: Dwyer, Henn: Homotopy theoretic methods in group cohomology. Explains various things including nerves, equivariant homotopy theory, transfer, the T-functor of Lannes
There are results by Suslin, Jardine, Karoubi and others about bijective maps between cohomology of classifying spaces computed in topological and discrete versions. See MR764100 for some discussion about when this holds and a profinite counterexample.
For classifying spaces of algebraic groups in the setting of A1-homotopy theory, see Morel-Voevodsky: A1-homotopy theory of schemes, chapter 4. Notion of etale classifying space, and relation to algebraic K-theory.
http://mathoverflow.net/questions/51694/history-of-classifying-spaces
ALGTOP discussion here, scroll down a bit.
<]]>- Closed monoidal categoryWrite comment View comments
Like a Monoidal category, but using the category of categories and adjunctions instead of the category of categories and functors. Get various 2-categories: Closed monoidal cats, closed symmetric monoidal cats, closed modules (or algebras) over a given closed symmetric monoidal category. See Hovey pp. 106.
Examples: Closed monoidal cats: Sets, R-mods, Bimod-R. Closed symmetric monoidal cats: k-spaces, CG spaces,
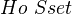 , the homotopy category of k-spaces.<]]>
, the homotopy category of k-spaces.<]]>- CoalgebraWrite comment View comments
- <]]>
- Cobordism hypothesisWrite comment View comments
- <]]>
- CocycleWrite comment View comments
- <]]>
- Coefficient groupWrite comment View comments
The coeffiecient group of a Generalized cohomology theory is defined to be
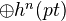 <]]>
<]]>- CofiberWrite comment View comments
In a pointed category with colimits and limits, we define the cofiber, or cokernel, of a map
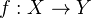 to be the coequalizer
to be the coequalizer 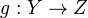 of
of  and the zero map.<]]>
and the zero map.<]]>- Cofiber sequenceWrite comment View comments
Let
 be a Pointed model category. A cofiber sequence in
be a Pointed model category. A cofiber sequence in 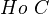 is a diagram
is a diagram 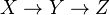 in
in 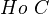 together with a right coaction of
together with a right coaction of  on
on 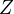 that is IMic in
that is IMic in 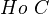 to a diagram of the form
to a diagram of the form 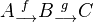 where
where  is a cofibration of cofibrant objects in
is a cofibration of cofibrant objects in  with cofiber
with cofiber 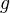 and where
and where  has the standard right coaction by
has the standard right coaction by 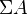 .
.To a cofiber sequence one can associate a boundary map
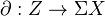 . See Hovey p. 156.
. See Hovey p. 156.Some further properties: Cofiber sequences are replete in
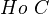 . The sequence
. The sequence 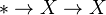 is a cofiber sequence. Any map fits as the first map in a cofiber sequence, and as the last in a fiber sequence. If
is a cofiber sequence. Any map fits as the first map in a cofiber sequence, and as the last in a fiber sequence. If  is a cofiber sequence, then
is a cofiber sequence, then 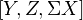 is too (must specify coaction here). Applying this last statement again and again gives a long exact sequence, called the Puppe sequence. If the first two maps are given between two cofiber sequences, can find a third map making everything commute. Also another fill-in statement. Verdier's octahedral axiom holds for a cofiber sequence. A left Quillen functor preserves cofiber sequences, and a right Quillen functor preserves fiber sequences. Both kind of sequences are preserved by the closed
is too (must specify coaction here). Applying this last statement again and again gives a long exact sequence, called the Puppe sequence. If the first two maps are given between two cofiber sequences, can find a third map making everything commute. Also another fill-in statement. Verdier's octahedral axiom holds for a cofiber sequence. A left Quillen functor preserves cofiber sequences, and a right Quillen functor preserves fiber sequences. Both kind of sequences are preserved by the closed  -module structure induced by the framing (i.e. "smashing" and "RHom").
-module structure induced by the framing (i.e. "smashing" and "RHom").The above properties are summarized in Hovey's def of pre-triangulated category, see page 170.
<]]>- Cofibrant objectWrite comment View comments
In a model category, an object is called cofibrant if the map from the initial object to it is a cofibration.
<]]>- Cofibrant replacementWrite comment View comments
In a Model category, the functorial factorization
 ensure that for any object
ensure that for any object  , the map
, the map 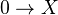 from the initial object factors through a cofibrant object, denoted by
from the initial object factors through a cofibrant object, denoted by 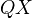 . This construction is a functor
. This construction is a functor 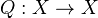 , called the cofibrant replacement functor.
, called the cofibrant replacement functor.http://mathoverflow.net/questions/54500/how-canonical-is-cofibrant-replacement
<]]>- Cofibrantly generatedWrite comment View comments
A model category is said to be cofibrantly generated if there are sets
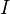 and
and 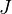 of maps such that
of maps such that- The domains of the maps of I are small relative to I-cell
- The domains of the maps of J are small relative to J-cell
- The class of fibrations is J-inj
- The class of trivial fibrations is I-inj
In this situtation, we refer to I as the set of generating cofibrations, and to J as the set of generating trivial cofibrations. A cofibrantly generated model category is called finitely generated if we can choose I and J so that the domains and codomains of I and J are finite relative to I-cell.
Here we have used the following abbreviations: Let I be class of morphisms in a category
 .
. - A morphism is I-injective if if it has the RLP wrt every morphism in I. Write I-inj for the class of such morphisms.
- A morphism is I-projective if if it has the LLP wrt every morphism in I. Write I-proj for the class of such morphisms.
- A morphism is an I-cofibration if it has the LLP wrt every I-injective morphism. Notation: I-cofib.
- A morphism is an I-fibration if it has the RLP wrt every I-projective morphism. Notation: I-fib.
- If
 has all small colimits, define I-cell to be the class of transfinite compositions of pushouts of elements of I. Remark: I-cell is contained in I-cof.
has all small colimits, define I-cell to be the class of transfinite compositions of pushouts of elements of I. Remark: I-cell is contained in I-cof.
Much more material on this is found in Hovey, Section 2.1. See for exampel Thm 2.1.19, which explains how cofibrantly generated model cats are constructed. We also get a criterion for when a functor is a Quillen functor.
For non-cofibrantly generated model cats, including examples and localization theorems, see the web page of Chorny
A cryptic note: Cofibrantly gen implies projective, and combinatorial implies injective. Does this refer to model structures on functor cats or what??
<]]>- CofibrationWrite comment View comments
Cofibrations are part of a model structure.
Cofibrations (trivial cofibrations) are closed under pushouts.
<]]>- Cohen-Lenstra heuristicsWrite comment View comments
arXiv:0912.4977 The Global Cohen-Lenstra Heuristic from arXiv Front: math.NT by Johannes Lengler The Cohen-Lenstra heuristic is a universal principle that assigns to each group a probability that tells how often this group should occur "in nature". The most important, but not the only, applications are sequences of class groups, which behave like random sequences of groups with respect to the so-called Cohen-Lenstra probability measure.
So far, it was only possible to define this probability measure for finite abelian $p$-groups. We prove that it is also possible to define an analogous probability measure on the set of \emph{all} finite abelian groups when restricting to the $\Sigma$-algebra on the set of all finite abelian groups that is generated by uniform properties, thereby solving a problem that was open since 1984.<]]>- Cohomological descentWrite comment View comments
David ZB on cohomology descent on the overconvergent site: http://front.math.ucdavis.edu/1204.5246
Weibel in Thomason's obituary
Weibel's Thomason obituary sketches the following things: For a diagram of spectra indexed by a small category J, the levelwise holims turn out to assemble to a spectrum, called the hypercohomology. Special cases: Hypercohomology of a complex of sheaves, homotopy fixed point spectrum. Explanation of Thomason's homotopy limit problem (special cases being the Segal conjecture and the Quillen-Lichtenbaum conjecture). For a presheaf
 , with values in spectra, we get the hypercohomology spectrum together with an augmentation map
, with values in spectra, we get the hypercohomology spectrum together with an augmentation map 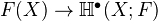 . Cohomological descent means that for every open
. Cohomological descent means that for every open 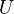 , the augmentation is a weak equivalence. Cohomological descent implies Mayer-Vietoris (the M-V square is homotopy cartesian), and for a Noetherian scheme of finite Krull dimension, cohomological descent for the Zariski topology is equivalent to M-V. There is also the hypercohomology spectral sequence, and special cases of this are explained to some extent.
, the augmentation is a weak equivalence. Cohomological descent implies Mayer-Vietoris (the M-V square is homotopy cartesian), and for a Noetherian scheme of finite Krull dimension, cohomological descent for the Zariski topology is equivalent to M-V. There is also the hypercohomology spectral sequence, and special cases of this are explained to some extent. At least for a scheme which is quasiprojective over a finite-dimensional Noetherian ring, we have the presheaf of Quillen K-theory spectra, and hence we can construct the corresponding Zariski and etale hypercohomology spectra. For
 regular, the Quillen K-theory spectrum has CD for the Zariski topology. For nonregular X, there is a fringing effect related to Bass K-groups which means that the Quillen K-theory spectrum cannot have CD, but it is the (-1)-connected cover of another K-theory spectrum (Bass?) which does have cohomological descent for the Zariski topology/ (still for any X q-proj over a fin-dim Noeth ring).
regular, the Quillen K-theory spectrum has CD for the Zariski topology. For nonregular X, there is a fringing effect related to Bass K-groups which means that the Quillen K-theory spectrum cannot have CD, but it is the (-1)-connected cover of another K-theory spectrum (Bass?) which does have cohomological descent for the Zariski topology/ (still for any X q-proj over a fin-dim Noeth ring).Can also consider K-theory with finite coefficients; it the homotopy groups of a certain spectrum, which can be described in many ways, for example as the smash product with the mod m Moore spectrum. Such a smash prod preserves cd, so the mod m spectrum also has Zariski cd as above.
More about the Quillen-Lichtenbaum conjecture:
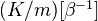 satisfies etale cohomological descent under some hypotheses. Comparison between K-theory and etale K-theory, see article for details.<]]>
satisfies etale cohomological descent under some hypotheses. Comparison between K-theory and etale K-theory, see article for details.<]]>- Cohomological functorWrite comment View comments
A functor from a triangulated category to an abelian category is called cohomological if for any distinguished triangle (X,Y,Z), the sequence
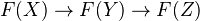 is exact.
is exact.See more under Triangulated category. See also the very last paragraph in Hovey's book, where he seems to define a different (more general???) notion of cohomology functor.
<]]>- Cohomological Hasse principleWrite comment View comments
- <]]>
- Cohomological physicsWrite comment View comments
- <]]>
- Cohomological purityWrite comment View comments
See Colliot-Thelene: Birational invariants, Purity, and the Gersten conjecture. In Proc. Symp. Pure Math. vol 58.1 (1995). Section 3.2.
(It's known for Dedekind schemes, and for
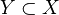 both smooth varieties, but a conjecture in general. Some work by Thomason?)<]]>
both smooth varieties, but a conjecture in general. Some work by Thomason?)<]]>- CohomologyWrite comment View comments
A somewhat bizarre entry, but wanted to include the nlab discussion: http://nlab.mathforge.org/nlab/show/cohomology
Could try to answer some of the following questions one day:
http://mathoverflow.net/questions/6125/what-is-a-cohomology-theory-seriously
http://mathoverflow.net/questions/27121/k-weil-cohomology-theories
<]]>- Cohomology in categoriesWrite comment View comments
Check Segal: Categories and cohomology theories. Topology 13 (1974), 293-312.
Cyclic homology of exact categories: Keller
Baues and Muro, see page 118. See perhaps also other things by Baues, e.g. Combinatorial foundations book.
A note by May on Grothendieck rings and Picard groups, and another note on caterads. See also K0409 and K0474.
Possibly of some interest: Nenashev, Garkusha, Davis and Lueck
Ulbrich: On cohomology of graded group categories. Compositio Mathematica, 63 no. 3 (1987)
<]]>- Cohomology operationWrite comment View comments
Consider two Generalized cohomology theories
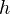 and
and  on CW pairs. A sequence of natural transformations
on CW pairs. A sequence of natural transformations 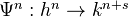 commuting with the connecting homomorphisms is called a natural transformation of degree
commuting with the connecting homomorphisms is called a natural transformation of degree  . If
. If 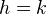 , call this a stable cohomology operation of degree
, call this a stable cohomology operation of degree  . There is a similar notion for Reduced cohomology theories.
. There is a similar notion for Reduced cohomology theories.Book: Cohomology Operations and Applications in Homotopy Theory, by Mosher and Tangora
<]]>- Cohomology popular writingsWrite comment View comments
- <]]>
- Combinatorial homotopy theoryWrite comment View comments
J. H. C. Whitehead, Combinatorial homotopy. I, Bull. Amer. Math. Soc. 55 (1949), 213-245. MR 11, #48.
<]]>- Combinatorial model categoryWrite comment View comments
http://ncatlab.org/nlab/show/combinatorial+model+category
http://ncatlab.org/nlab/show/combinatorial+simplicial+model+category
http://golem.ph.utexas.edu/category/2009/11/combinatorial_model_categories.html
<]]>- Commutative algebraWrite comment View comments
Add good references, for example:
Atiyah and MacDonald (link?). Solution are here
Eisenbud
Lots of other books in the Commutative algebra folder under ALGEBRA
Serre: Local algebra. French version in LNM0011
Dieudonne: Topics in local algebra
<]]>- Compact objectWrite comment View comments
http://ncatlab.org/nlab/show/compact+object+in+an+(infinity,1)-category
http://ncatlab.org/nlab/show/small+object
I think, but may be completely wrong, that compact would mean constructible for sheaves of sets, and perfect for complexes of abelian sheaves. In motivic homotopy theory, I believe that suspension spectra of smooth schemes are compact.
MO questions with several nice answers and a link to an nLab summary: http://mathoverflow.net/questions/59282/sums-compact-objects-f-g-objects-in-categories-of-modules
<]]>- Compactly generated categoryWrite comment View comments
- <]]>
- Completions of categoriesWrite comment View comments
The problem of "completing" a category is discussed in LNM0024. Here Lambek discusses notions like sup-complete and many other things, and also some drawbacks of the naive presheaves approach (some stuff is not preserved by this). A related problem was mentioned by Bondal in the Grothendieck conference talk Jan 2009, and he used this to motivate the introduction of Groth topologies, and the use of sheaves instead of presheaves.
<]]>- Complex manifoldsWrite comment View comments
I think there is a very nice book by Huybrechts
Complex manifolds folder in Geometry. Many nice things, for example Global aspects of complex geometry.
http://mathoverflow.net/questions/4895/the-relationship-between-complex-and-algebraic-geomety
Larusson: The cat of complex manifolds can be embedded into a model cat in a way such that a manifold is cofibrant iff it is Stein, and fibrant iff it is Oka. See AMS Notice Jan 2010: What is an Oka manifold. Original article not referenced.
<]]>- Complex multiplicationWrite comment View comments
LNM0021: Seminar on CM, Serre, Iwawasa et al.
http://mathoverflow.net/questions/99322/books-or-notes-on-complex-multiplication
Book by Taniyama and Shimura, in the AV folder.
<]]>- Complex structureWrite comment View comments
Appendix 4.7 of Felix, Oprea, Tanre in Homotopy th folder: Basic Hermitian and symplectic linear algebra, and basic notions of complex structures.
Deformations of complex structures: Original papers by Kodaira. Book: Grundlehren 283, Springer.
<]]>- Computational algebraic geometryWrite comment View comments
MEGA is the acronym for Effective Methods in Algebraic Geometry (and its equivalent in Italian, French, Spanish, German, Russian, etc.), a series of roughly biennial conferences on computational and application aspects of Algebraic Geometry and related topics with very high standards. Previous meetings were held in 1990 (Castiglioncello, Italy), 1992 (Nice, France), 1994 (Santander, Spain), 1996 (Eindhoven, Nederlands), 1998 (St. Malo, France) 2000 (Bath, United Kingdom), 2003 (Kaiserslautern, Germany), 2005 (Porto Conte, Italy) and 2007 (Strobl, Austria).
Proceedings containing a selection of the papers and invited talks presented at previous Mega conferences have been published by Birkhäuser in the series Progress in Mathematics (volumes no. 94, 109 and 143), by the Journal of Pure and Applied Algebra (volumes no. 117 and 118, 139 and 164) and by the Journal of Symbolic Computation (volumes no. 39 3-4 and 42 1-2).
Refs for computing de Rham cohomology of a complex variety: http://arxiv.org/pdf/0905.2212v1
Stillman et al ed: Software for algebraic geometry
Title: Effective computation of Picard groups and Brauer-Manin obstruction of degree two K3 surfaces over number fields Authors: Brendan Hassett, Andrew Kresch, Yuri Tschinkel http://front.math.ucdavis.edu/1203.2214 Categories: math.AG Algebraic Geometry Comments: 15 pages MSC: 14G25 (primary), 14F22, 14J28 (secondary) Abstract: Using the Kuga-Satake correspondence we provide an effective algorithm for the computation of the Picard and Brauer groups of K3 surfaces of degree 2 over number fields
arXiv:1205.5896 Approximate computations with modular curves from arXiv Front: math.AG by Jean-Marc Couveignes, Bas Edixhoven This article gives an introduction for mathematicians interested in numerical computations in algebraic geometry and number theory to some recent progress in algorithmic number theory, emphasising the key role of approximate computations with modular curves and their Jacobians. These approximations are done in polynomial time in the dimension and the required number of significant digits. We explain the main ideas of how the approximations are done, illustrating them with examples, and we sketch some applications in number theory.
<]]>- Computational algebraic topologyWrite comment View comments
[An excellent set of notes by Sergeraert.
Computational homology, by Kaczynski, Mischaikow, Mrozek. Springer
http://mathoverflow.net/questions/57166/computational-software-in-algebraic-topology
http://mathoverflow.net/questions/22232/which-properties-of-finite-simplicial-sets-can-be-computed
arXiv:1208.3816 Constructive Homological Algebra and Applications from arXiv Front: math.KT by Julio Rubio, Francis Sergeraert This text was written and used for a MAP Summer School at the University of Genova, August 28 to September 2, 2006. Available since then on the web site of the second author, it has been used and referenced by several colleagues working in Commutative Algebra and Algebraic Topology. To make safer such references, it was suggested to place it on the Arxiv repository.
It is a relatively detailed exposition of the use of the Basic Perturbation Lemma to make constructive Homological Algebra (standard Homological Algebra is not constructive) and how this technology can be used in Commutative Algebra (Koszul complexes) and Algebraic Topology (effective versions of spectral sequences).arXiv:1206.4345 Geometric Objects and Cohomology Operations from arXiv Front: math.AT by Rocio Gonzalez-Diaz, Pedro Real Cohomology operations (including the cohomology ring) of a geometric object are finer algebraic invariants than the homology of it.
In the literature, there exist various algorithms for computing the homology groups of simplicial complexes but concerning the algorithmic treatment of cohomology operations, very little is known. In this paper, we establish a version of the incremental algorithm for computing homology which saves algebraic information, allowing us the computation of the cup product and the effective evaluation of the primary and secondary cohomology operations on the cohomology of a finite simplicial complex. We study the computational complexity of these processes and a program in Mathematica for cohomology computations is presented.<]]>- Computational mathematicsWrite comment View comments
Oberwolfach software references
Towards computer-aided real mathematics
http://mathoverflow.net/questions/119/is-there-a-good-computer-package-for-working-with-bicomplexes
http://mathoverflow.net/questions/3044/tools-for-collaborative-paper-writing
"The chrome extension GmailTeX allows one to render TeX in messages received, or live as you compose a message"
<]]>- Computing cohomologyWrite comment View comments
http://mathoverflow.net/questions/19846/a-list-of-machineries-for-computing-cohomology
http://mathoverflow.net/questions/33315/lists-of-computed-cohomologies
<]]>- Computing zeta functionsWrite comment View comments
Over finite fields: Check Kedlaya's webpage.
A preprint using rigid cohomology: http://front.math.ucdavis.edu/1110.4049
<]]>- Conformal field theoryWrite comment View comments
http://nlab.mathforge.org/nlab/show/conformal+field+theory
For conformal field theory and other types of field theory: Check out the MO answers of Ben-Zvi.
<]]>- ConiveauWrite comment View comments
See Gillet: K-theory and Intersection theory
There is also something in the K-theory handbook
A very nice paper by Levine on the homotopy coniveau filtration.
Kahn et al: The Bloch-Ogus-Gabber theorem. Gives a general argument for many different CTs at once.
arXiv:0907.3535 Coniveau filtrations and finite dimensionality for pure motives from arXiv Front: math.AG by Charles Vial Let $X$ be a smooth projective variety over a field $k \subset \C$. We define a coniveau filtration $\widetilde{N}$ -- a priori different from the usual coniveau filtration $N$ -- on the singular cohomology of $X$ with rational coefficients. If $X$ satisfies the Lefschetz conjecture B, we prove that the projectors on the filtered pieces of the cohomology of $X$ are induced by algebraic correspondences. If moreover $X$ is finite dimensional in the sense of Kimura (for example, $X$ could be any abelian variety or any finite quotient thereof) the Chow motive of $X$ admits a refined Chow-Künneth decomposition lifting the coniveau grading on the cohomology of $X$ and we study the behavior of the Chow groups of $X$ under this decomposition. As an application, we give several conjectural descriptions of the rational Chow groups of $X$ depending on the support of the cohomology groups of $X$. We also consider the case where $k$ is an arbitrary field. Results valid in characteristic zero extend to positive characteristic if one is ready to admit that the Lefschetz conjecture holds in general.
<]]>- ConnectionWrite comment View comments
Ref: Geometry and Topology of Manifolds, Banach Center Pub Vol 76
Cohomology, Connections, Curvature and Characteristic classes: Mond
LNM0163 Deligne lectures on local systems, integrable connections, Gauss-Manin conn, differential eqs, regularity at infinity, etc.
http://nlab.mathforge.org/nlab/show/connection
nLab connection on a bundle
http://www.ncatlab.org/nlab/show/Grothendieck+connection
http://ncatlab.org/nlab/show/connection+for+coring
http://ncatlab.org/nlab/show/connection+for+a+differential+graded+algebra
<]]>- ConnectiveWrite comment View comments
Someone (maybe Gepner) said somewhere that connective (E-infty spectra??) are (more or less??) group-like (E-infty spectra/S-modules)
<]]>- ConnesWrite comment View comments
- <]]>
- Connes-Consani theoryWrite comment View comments
arXiv:1103.4672 On the arithmetic of the BC-system from arXiv Front: math.NT by Alain Connes, Caterina Consani For each prime p and each embedding of the multiplicative group of an algebraic closure of Fp as complex roots of unity, we construct a p-adic indecomposable representation of the integral BC-system as additive endomorphisms of the big Witt ring of an algebraic closure of Fp. The obtained representations are the p-adic analogues of the complex, extremal KMS states at zero temperature of the BC-system. The role of the Riemann zeta function, as partition function of the BC-system over complex numbers is replaced, in the p-adic case, by the p-adic L-functions and the polylogarithms whose values at roots of unity encode the KMS states. We use Iwasawa theory to extend the KMS theory to a covering of the completion of an algebraic closure of the p-adic field. We show that our previous work on the hyperring structure of the adeles class space, combines with p-adic analysis to refine the space of valuations on the cyclotomic extension of Q as a noncommutative space intimately related to the integral BC-system and whose arithmetic geometry comes close to fulfill the expectations of the "arithmetic site". Finally, we explain how the integral BC-system appears naturally also in de Smit and Lenstra construction of the standard model of an algebraic closure of F_p which singles out the subsystem associated to the Z^-extension of Q.
<]]>- ConsaniWrite comment View comments
- <]]>
- Constructible sheavesWrite comment View comments
These should be the compact objects!!
<]]>- Continuous functorWrite comment View comments
- <]]>
- CortinasWrite comment View comments
- <]]>
- Cosmic Galois groupWrite comment View comments
arXiv:1108.4627 The Cosmic Galois group as Koszul dual to Waldhausen's A(pt) from arXiv Front: math.AT by Jack Morava K. Hess's theory of homotopical descent, applied to the large categories of motives defined recently by Blumberg, Gepner, and Tabuada, suggests that the Koszul dual of Waldhausen's K-theory of the sphere spectrum, regarded as a supplemented algebra via the Dennis trace, plays a very general role as a kind of motivic group.
After tensoring with the rationals, the resulting Hopf algebra has close relations to the ring of quasi-symmetric functions and work of Baker and Richter on one hand, and on the other to work of Deligne and others on the motivic group for mixed Tate motives.<]]>- Cotangent bundleWrite comment View comments
- <]]>
- Cotangent complexWrite comment View comments
See Illusie.
http://ncatlab.org/nlab/show/cotangent+complex
http://mathoverflow.net/questions/2607/intuition-about-the-cotangent-complex
Groth in LNM0079 on relative cot complex and additive cofibred cats
An excellent introduction to derived AG is the CRM 2008 notes, in Toen web unpublished folder. These notes also covers algebraic stacks, the idea of moduli spaces, a little about cotangent complexes, and examples of derived algebraic stacks.
arXiv:1008.0601 A note on the cotangent complex in derived algebraic geometry from arXiv Front: math.AT by Gabriele Vezzosi This note is supposed to answer some questions on deformation theory in derived algebraic geometry. We show that derived algebraic geometry allows for a geometrical interpretation of the full cotangent complex and gives a natural setting for deformation and obstruction theories.
<]]>- CoxWrite comment View comments
- <]]>
- CraneWrite comment View comments
- <]]>
- Cross functorsWrite comment View comments
Online lectures by Voevodsky
<]]>- Crossed complexWrite comment View comments
Many things by Ronald Brown, for example: The classifying spaces of a crossed complex (el)
Many papers by Pirashvili, have not bothered to download.
<]]>- Crossed modulesWrite comment View comments
See Baues: Homotopy types, for their role in homotopy theory.
The category of crossed modules is equivalent to the category of internal categories in Grp.
I think this might be the same thing as Crossed complex nLab (almost, see the link for explanation)
<]]>- CrystalWrite comment View comments
- <]]>
- Crystalline representationWrite comment View comments
[arXiv:0907.0221] Local constancy for the reduction mod p of 2-dimensional crystalline representations from arXiv Front: math.NT by Laurent Berger Irreducible crystalline representations of dimension 2 of Gal(Qpbar/Qp) depend up to twist on two parameters, the weight k and the trace of frobenius ap. We show that the reduction modulo p of such a representation is a locally constant function of ap (with an explicit radius) and a locally constant function of the weight k if a_p <> 0. We then give an algorithm for computing the reductions modulo p of these representations. The main ingredient is Fontaine's theory of (phi,Gamma)-modules as well as the theory of Wach modules.
<]]>- Cubical objectWrite comment View comments
- <]]>
- Cubical setWrite comment View comments
http://nlab.mathforge.org/nlab/show/cubical+set
From ALG-TOP Sep 2009, very interesting
(there might also be further follow-up emails)
I am enquiring about the history of cubical and simplicial sets, and would be grateful for any corrections/additions/references for the following account. As I do not have sure contact details with Dan Kan I am posting this generally, and would be very happy to have his or other account.
- Dan Kan's first work on abstract homotopy was cubical and published as @article {Kan55, AUTHOR = {Kan, D. M.}, TITLE = {Abstract homotopy. {I}}, JOURNAL = {Proc. Nat. Acad. Sci. U.S.A.}, VOLUME = {41}, YEAR = {1955}, PAGES = {1092--1096}, MRCLASS = {55.0X}, % MRNUMBER = {18,142d}, MRREVIEWER = {J. C. Moore}, }
However his second paper was simplicial, and I remember being told in the 1950s as a research student that reasons for abandoning the cubical approach were (i) the geometric realisation of I x I in cubical terms had non trivial homotopy type, and (ii) John Milnor had successfully written on the geometric realisation of simplicial sets, and in particular on the product.
Was the example in (i) ever published or remarked on in some form near that time; it is in quite recent work by Rick Jardine in HHA.
Ronnie Brown
Thanks for all the helpful comments.
I talked to Dan Kan on the phone last night - we first met in Oxford over 50 years ago!
He confirmed that the reasons for giving up the cubical theory in the 1950s were 1. Normalisation of the chains was essential. 2. Cubical groups were not fibrant. 3. The geometric realisation of I x I had the wrong homotopy type.
No getting round 1. A relevant reference is @article {antolini-weist, AUTHOR = {Antolini, Rosa and Wiest, Bert}, TITLE = {The singular cubical set of a topological space}, JOURNAL = {Math. Proc. Cambridge Philos. Soc.}, FJOURNAL = {Mathematical Proceedings of the Cambridge Philosophical Society}, VOLUME = {126}, YEAR = {1999}, NUMBER = {1}, PAGES = {149--154}, ISSN = {0305-0041}, CODEN = {MPCPCO}, MRCLASS = {55U10 (55U15)}, MRNUMBER = {MR1681660 (2000e:55014)}, MRREVIEWER = {Stanley Kochman}, }
A relevant reference for 2. is @article {tonks-cubgps, AUTHOR = {Tonks, A. P.}, TITLE = {Cubical groups which are {K}an}, JOURNAL = {J. Pure Appl. Algebra}, FJOURNAL = {Journal of Pure and Applied Algebra}, VOLUME = {81}, YEAR = {1992}, NUMBER = {1}, PAGES = {83--87}, ISSN = {0022-4049}, CODEN = {JPAAA2}, MRCLASS = {55U10 (18D35 18G30)}, MRNUMBER = {MR1173825 (93h:55013)}, MRREVIEWER = {Marek Golasi{\'n}ski}, } which shows cubical groups with
connections' introduced by Higgins and me, in order to formulate the notion ofThe command "%" is illegal in math mode (perhaps you intended to use "\%" instead?)connections' (see below) are Kan. Various extra structures on cubical sets are discussed in @article {Grandis-cubsite, AUTHOR = {Grandis, M. and Mauri, L.}, TITLE = {Cubical sets and their site}, JOURNAL = {Theory Applic. Categories}, FJOURNAL = {Theory and Applications of Categories}, VOLUME = {11}, YEAR = {2003}, PAGES = {185-201}, MRCLASS = {}, % MRNUMBER = {39 \#952}, MRREVIEWER = {}, } including the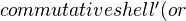 cube'). (You get extra types of `degenerate' cubes using the monoid structure max on the unit interval.) A major reason for using cubes was the easy notion of multiple compositions, tricky in simplicial or globular theories. Another reason was easy homotopies. See our papers in JPAA.
cube'). (You get extra types of `degenerate' cubes using the monoid structure max on the unit interval.) A major reason for using cubes was the easy notion of multiple compositions, tricky in simplicial or globular theories. Another reason was easy homotopies. See our papers in JPAA.
- now is OK according to recent work of Maltsiniotis on cubical sets with connection, which develops work of section 8.4 of @article {cisinski-ast, AUTHOR = {Cisinski, Denis-Charles}, TITLE = {Les pr\'efaisceaux comme mod`eles des types d'homotopie}, JOURNAL = {Ast\'erisque}, FJOURNAL = {Ast\'erisque}, NUMBER = {308}, YEAR = {2006}, PAGES = {xxiv+390}, ISSN = {0303-1179}, ISBN = {978-2-85629-225-9}, MRCLASS = {55-02 (18F20 18G50 55P60 55U35)}, MRNUMBER = {MR2294028 (2007k:55002)}, MRREVIEWER = {Philippe Gaucher}, } H. Federer had some useful `Lecture Notes on Algebraic Topology' (Brown University, 1962) which it would be good to have available as a scan. Of course cubical homology was used by Serre, and in books by Hilton and Wylie, and by Massey.
See also I. Patchkoria on derived functors: arXiv: 0907.1905, which uses `pseudo-connections'.
Ronnie Brown
<]]>- Cup productWrite comment View comments
- <]]>
- CurtisWrite comment View comments
- <]]>
- Curtis spectral sequenceWrite comment View comments
arXiv:0910.2817 Derived functors of non-additive functors and homotopy theory from arXiv Front: math.AT by Lawrence Breen, Roman Mikhailov We develop a functorial approach to the study of the homotopy groups of spheres and Moore spaces $M(A,n)$, based on the Curtis spectral sequence and the decomposition of Lie functors as iterates of simpler functors such as the symmetric or exterior algebra functors. The discussion takes place over the integers, and includes a functorial description of the derived functors of certain Lie algebra functors, as well as of all the main cubical functors (such as the degree 3 component $SP^3$ of the symmetric algebra functor). As an illustration of this method, we retrieve in a purely algebraic manner the 3-torsion component of the homotopy groups of the 2-sphere up to degree 14, and give a unified presentation of homotopy groups $\pi_i(M(A,n))$ for small values of both $n$ and $i$.
<]]>- CW complexWrite comment View comments
References:
- Cellular Structures in Topology (Cambridge Studies in Advanced Mathematics) by Rudolf Fritsch
<]]>- Cyclic categoryWrite comment View comments
- <]]>
- Cyclotomic unitsWrite comment View comments
Soulé on cyclotomic units in Asterisque 147-148 MR891430, seems to be a really nice paper, on groups of cyclotomic units in odd K-groups of rings of integers, and relation to p-adic regulators and p-adic L-functions.
<]]>- Cylinder objectWrite comment View comments
In a model category, a cylinder object for an object
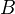 is a factorisation of the fold map
is a factorisation of the fold map 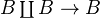 into a cofibration followed by a WE. The functorial factorisations provide a functorial cylinder object, denoted by
into a cofibration followed by a WE. The functorial factorisations provide a functorial cylinder object, denoted by 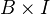 .<]]>
.<]]>