Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- D-modulesWrite comment View comments
See Alex Shannon's essay.
Last chapter of Gelfand-Manin: Algebra V
http://ncatlab.org/nlab/show/D-module
http://ncatlab.org/nlab/show/D-geometry
arXiv:1206.1435 Three lectures on Algebraic Microlocal Analysis from arXiv Front: math.AG by Pierre Schapira These three lectures present some fundamental and classical aspects of microlocal analysis. Starting with the Sato's microlocalization functor and the microsupport of sheaves, we then construct a microlocal analogue of the Hochschild homology for sheaves and apply it to recover index theorems for D-modules and elliptic pairs. In the third lecture, we construct the ind-sheaves of temperate and Whitney holomorphic functions and give some applications to the study of irregular holonomic D-modules.
<]]>- Dagger categoryWrite comment View comments
- <]]>
- de JeuWrite comment View comments
- <]]>
- de JongWrite comment View comments
- <]]>
- de Rham complexWrite comment View comments
- <]]>
- de Rham-Witt complexWrite comment View comments
Lots of articles by Hesselholt and others. Older work by Deligne, Illusie, Bloch. Perhaps something in the K-theory handbook.
<]]>- DedekindWrite comment View comments
3 volumes of his works
<]]>- Deformation of complex structuresWrite comment View comments
For this and Maurer-Cartan equations, see Huybrechts book in Complex manifolds folder. See also Kodaira in same folder.
Deformations of complex structures: Original papers by Kodaira. Book: Grundlehren 283, Springer.
<]]>- Deformation theoryWrite comment View comments
Sernesi: Deformations of algebraic schemes
New book by Hartshorne
A series of arxiv preprints by Orlov.
http://mathoverflow.net/questions/40574/innovations-in-deformation-theory
Jonathan Wise: Obstruction theories and virtual fundamental classes. http://front.math.ucdavis.edu/1111.4200
Thesis of Illusie
Introduction to singularities and deformations, Greuel et al, Springer
http://nlab.mathforge.org/nlab/show/deformation+theory
http://mathoverflow.net/questions/5364/what-is-a-deformation-of-a-category
http://mathoverflow.net/questions/570/deformation-theory-of-representations-of-an-algebraic-group
Greuel et al: Introduction to Singularities and Deformations (Springer Monographs in Mathematics)
Green, Griffiths: Formal Deformation of Chow Groups. In Abel volume.
http://mathoverflow.net/questions/33526/deformations-and-the-dual-numbers
<]]>- DegliseWrite comment View comments
See Déglise
<]]>- DeligneWrite comment View comments
Some publications
- Deligne-Mumford: The irreducibility of the space of curves of given genus
- Deligne: Hodge cycles on abelian varieties (notes by Milne), 1982, in LNM900.
- Deligne: Décompositions dans la catégorie dérivée (in the Motives volumes)
- Categories spectrales (manuscript, 1968)
- Letters to Illusie, Oct 1973 and Oct 1976
<]]>- Deligne-Mumford stackWrite comment View comments
Toen: On motives for DM stacks. Discusses Chow rings and Chow motives, 2 different defs. Motivation: Gromov-Witten invariants.
<]]>- DeloopingWrite comment View comments
http://mathoverflow.net/questions/41525/how-should-i-think-about-delooping
See the article in K-theory handbook on deloopings, in vol 1
arXiv:1304.0557 Delooping of relative exact categories fra arXiv Front: math.CT av Toshiro Hiranouchi, Satoshi Mochizuki We introduce a delooping model of relative exact categories. It gives us a condition that the negative K-group of a relative exact category becomes trivial.
<]]>- DemazureWrite comment View comments
- <]]>
- Dendroidal setWrite comment View comments
See Moerdijk excellent Barcelona notes, in Toen folder.
<]]>- DeningerWrite comment View comments
- <]]>
- DerivatorWrite comment View comments
http://nlab.mathforge.org/nlab/show/derivator
Groth: Monoidal derivators and additive derivators
arXiv:1101.4144 Homotopical exact squares and derivators from arXiv Front: math.CT by Georges Maltsiniotis The aim of this paper is to generalize in a homotopical framework the notion of exact square introduced by René Guitart, and explain the relationship between this generalization and the theory of derivators.
[arXiv:1212.3277] The additivity of traces in monoidal derivators from arXiv Front: math.AT by Moritz Groth, Kate Ponto, Michael Shulman We develop the theory of monoidal structures on derivators, culminating in a proof that generalized trace maps in a closed symmetric monoidal stable derivator are additive along distinguished triangles. This includes the additivity of classical Euler characteristics and Lefschetz numbers, as well as many generalizations of these invariants.
The proof of additivity closely follows that of May for triangulated categories, but the derivator context makes the underlying ideas more transparent, showcasing the advantages of derivators over triangulated categories, model categories, and (infinity,1)-categories. We expect many other generalizations of classical stable results to be possible in this context as well.<]]>- Derived algebraic geometryWrite comment View comments
http://mathoverflow.net/questions/37825/what-are-jacob-luries-key-insights
See Toen: Essen talk, for intro to his ideas, including refs to dg schemes, and a reasonable amount of substance on derived moduli stacks towards the end.
http://mathoverflow.net/questions/55053/complicating-an-example-by-toen-motivations-for-dag
An excellent introduction to derived AG is the CRM 2008 notes, in Toen web unpublished folder. These notes also covers algebraic stacks, the idea of moduli spaces, a little about cotangent complexes, and examples of derived algebraic stacks.
nlab on derived noncomm geom
nlab on DAG
http://mathoverflow.net/questions/30396/derived-algebraic-geometry-and-chow-rings-chow-motives
arXiv:1208.6325 Grothendieck-Riemann-Roch for derived schemes from arXiv Front: math.AG by Parker Lowrey, Timo Schürg We define bivariant algebraic K-theory and bivariant derived Chow on the homotopy category of derived schemes over a smooth base. The orientation on the latter corresponds to virtual Gysin homomorphisms. We then provide a morphism between these two bivariant theories and compare the two orientations. This comparison then yields a homological and cohomological Grothendieck-Riemann-Roch formula for virtual classes.
<]]>- Derived categorical sheavesWrite comment View comments
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. Notion of derived cat sheaves, a categorification of the notion of complexes of sheaves of O-modules on schemes (also quasi-cohomology and perfect versions). Chern character for these categorical sheaves, a categorified version of the Chern char for perfect complexes with values in cyclic homology. Using the derived loop space. "This work can be seen as an attempt to define algebraic analogues of of elliptic objects and char classes for them". 1. Motivations: Elliptic cohomology, geometric interpretations, chromatic level and n-categorical level, 2-VBs. Maybe the typical generalized CT of chromatic level n should be related to n-cats, more precisely cohomology classes should be rep by maps from X to a certain n-stack. Rognes red-shift conjecture: Intuitively saying that the K-th spectrum of a commutative ring spectrum of chrom level n is of chrom level (n+1). More on ell cohomology and 2-cats. Idea of categorical sheaves: For X a scheme, should have a symmetric monoidal 2-cat Cat(X) which is a categorification of Mod(X), in the sense that Mod(X) should be the cat of endomorphisms of the unit objects in Cat(X). More details. Notions of secondary cohomology and secondary K-theory. Notion of derived categorical sheaves, more reasonable than nonderived version. Relation between
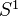 -equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.<]]>
-equivariant functions on LX and negative cyclic homology. 2. Categorification of homological algebra and dg-cats. 3. Loop spaces in DAG. More, including relations with variations of Hodge structures. Final remark on algebraic elliptic cohomology. "Algebraic K-theory determines complex topological K-theory", ref to Walker 2002.<]]>- Derived categories in algebraic geometryWrite comment View comments
Many articles by Bridgeland.
http://ncatlab.org/nlab/show/reconstruction+theorem
Orlov paper on representability of eqiovalences by objects on the product
About moduli for higher-dimensional varieties: Toen and Anel prove that the number of iso classes of smooth projective complex alg vars with the same derived cat must be countable. File Toen web publ dgcat-alg.pdf. They use some kind of (nonalgebraic) stack which in some sense is a moduli space for smooth projective varieties.
http://front.math.ucdavis.edu/0912.4040 Title: Derived invariance of the number of holomorphic 1-forms and vector fields. Authors: Mihnea Popa, Christian Schnell. Abstract: We prove that smooth projective varieties with equivalent derived categories have isogenous (and sometimes isomorphic) Picard varieties. In particular their irregularity and number of independent vector fields are the same. This is turn implies, in combination with the invariance of Hochschild homology, that all Hodge numbers are the same for arbitrary derived equivalent threefolds, as well as other consequences of derived equivalence based on numerical criteria.
<]]>- Derived categoryWrite comment View comments
References
arXiv:1206.6632 A Course on Derived Categories from arXiv Front: math.CT by Amnon Yekutieli These are notes for an advanced course given at Ben Gurion University in Spring 2012.
Caldararu in Homol alg folder (good!)
http://www.ncatlab.org/nlab/show/derived+category
On derived cats in terms of model cats: http://mathoverflow.net/questions/372/derived-categories-and-homotopy-categories
Krause lectures, in Homological algebra folder
Hartshorne LNM0020
Keller chapter in Handbook of Algebra vol 1, in Various folder under ALGEBRA
An appendix to Hartshorne: Residues and duality
Huybrechts: Fourier-Mukai transform in algebraic geometry (book)
Notes by Dolgachev, in Homological algebra folder
Gelfand-Manin: Algebra V
Gelfand and Manin: Methods book
Bondal-Orlov in Compositio
The derived category of R-modules is the homotopy category of the model category of chain complexes of R-modules.
Can define the derived category of an exact category: see Laumon in LNM 1016.
For brief intro, and longer treatment of equivariant derived cats, see Bernstein and Lunts, in Homol alg folder.
A nice note by May
Ask Bao for other refs. Bao said that automorphisms of the derived cat are just (3) the shifts (
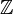 ) times the semidirect product of (2) automorphisms of the variety and (3) twists with (any???) line bundles)
) times the semidirect product of (2) automorphisms of the variety and (3) twists with (any???) line bundles)Here are some notes by Murfet:
- Derived categories Part I
- Derived categories Part II
- Derived categories of sheaves
- Derived categories of quasi-coherent sheaves
Definition and properties
Memo: Let
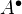 be a complex of abelian groups. Then
be a complex of abelian groups. Then 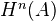 is the set of homotopy classes of maps from
is the set of homotopy classes of maps from 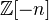 to
to 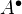 . Here I think the first complex is
. Here I think the first complex is  places in degree
places in degree  . (And when writing down a complex, the degree increases as one goes to the right - I think this means that the complex is cohomological.)
. (And when writing down a complex, the degree increases as one goes to the right - I think this means that the complex is cohomological.)Discussion with Scholl, Nov 2007
Can think of
 as the complexes of injectives in
as the complexes of injectives in 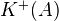 . For
. For 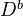 , think complexes of injectives, which have bounded cohomology.
, think complexes of injectives, which have bounded cohomology.More references
LECTURES ON DERIVED AND TRIANGULATED CATEGORIES 33 [Li] J. Lipman, Notes on derived categories and derived functors, available at http://www.math.purdue.edu/lipman.
A list of references in an article by Orlov, related to the derived category of coherent sheaves on a variety.
J.-L. Verdier, Des categoryégories dérivées des categoryégories abéliennes, Astérisque 239, 1996.
A. Rosenberg, The spectrum of abelian categories and reconstructions of schemes, in Rings, Hopf Algebras, and Brauer groups, 257-274, Lectures Notes in Pure and Appl. Math. 197, Marcel Dekker, New York, 1998.
[Ke1] B. Keller, Introduction to abelian and derived categories, in Representations of reductive groups, edited by R. W. Carter and M. Geck, Cambridge University Press 1998, 41-62 (available on Keller's webpage).
[Ke2] B. Keller, Derived categories and their uses, in Handbook of algebra, edited by M. Hazewinkel, Elsevier 1996 (available on Keller's webpage).
An essay topic from Grojnowski
The aim of this essay is to give an introduction to homological algebra, as it is applied in algebraic geometry and string theory (homological mirror symmetry), and/or in representation theory. As well as learning some abstract machinery, you will be gaining proficiency in either computing cohomology of coherent sheaves (geometry), or in representation theory (quivers, symplectic reflection algebras, finite groups). The category of representations of an algebra, or of coherent sheaves on an algebraic variety, is an abelian category; its derived category is built out of the category of chain complexes of such objects. Cutting your abelian category into pieces (for example, by partitioning your variety into an open subvariety and its closed complement) allows you to cut the derived category into pieces, but the derived category has ’more’ decompositions than the abelian. Moreover, different abelian categories may have the same derived category. There are two ways into this essay, for those with and without algebraic geometry. If you know some algebraic geometry: Begin with Fourier-Mukai transform, which is an involution on the derived category of an elliptic curve. Use this to describe all vector bundles on an elliptic curve. More generally, do this for abelian varieties. A nice consequence is the Torelli theorem. Then back up, and learn classical Koszul duality, the derived equivalence between modules for SV and ^V ; as well as Beilinson’s theorem describing all sheaves on Pn. ADHM correspondence, describing quiver moduli spaces. After this, try some explicit examples of flops by blowing up and down; this is due to Bondal- Orlov. You can continue in this way, and learn some of the derived category approach to 27 birational geometry. Some lovely classical computations can be studied in this language; see for example the papers of Kuznetsov. This is probably enough for an essay, but if you’re ambitious: Then read Bridgeland’s paper constructing smooth 3-fold flops as the moduli space of perverse point sheaves. Other nice examples of derived categories were inspired by physics; they are called Landau- Ginzburg models. These are an avatar of coherent sheaves on the space of vanishing cycles of a function f : X ! C, and were constructed by Orlov and Kontsevich. You may wish to play with these. At this point, you should read Bridgeland’s papers on stability conditions. He constructs a complex variety attached to an abelian or derived category, each point of which parameterizes a t-structure and a notion of stability condition. You should compute these spaces (or follow the computations in the literature!) for a line bundle over P2, at least. If you don’t know any algebraic geometry, this is still a good essay — derived equivalences are at the heart of representation theory — but the examples you should work with are representations of groups, or quivers, or Hecke algebras. One very rich source of examples are the ’cluster algebras’ of Fomin-Zelevinsky; Keller’s survey paper (listed below) is a fun introduction. But if you are interested in this essay, come talk to me and we’ll find a way into the subject that works best with your background. References For the basics of homological algebra, the textbooks of Weibel and Gelfand & Manin. Some survey papers: [1] Bridgeland, Spaces of stability conditions, arxiv/0611510 Bridgeland, Derived categories of coherent sheaves, arxiv/0602129 Bondal & Orlov, Derived categories of coherent sheaves, arxiv/0206295 [2] Keller, Cluster algebras, quiver representations and triangulated categories, arxiv/0807.1960
<]]>- Derived category of coherent sheavesWrite comment View comments
Several arxiv preprints by Orlov, including one discussing the relation with motives.
<]]>- Derived deformation theoryWrite comment View comments
[arXiv:0908.1963] Derived deformations of schemes from arXiv Front: math.AG by J. P. Pridham We introduce a new approach to constructing derived deformation groupoids, by considering them as parameter spaces for strong homotopy bialgebras. This allows them to be constructed for all classical deformation problems, such as deformations of an arbitrary scheme, in any characteristic.
<]]>- Derived functorWrite comment View comments
See Murfet
According to Weibel, (p. 29) a notion of left derived functor can be defined for any functor from a category to an abelian category, as long as the domain is closed under finite limits and has enough projective objects.
Derived functors are examples of Kan extensions, see MacLane.
Eilenberg: Bourbaki exp 46
Derived functors can be defined in the more general setting of homotopical algebra nLab
One can talk about versions of derived functors in settings without enough projectives or injectives. See eg Buchsbaum in LNM0061, and maybe ask Julia.
Tierney and Vogel in LNM0086 talks about deriving any functor from a cat with finite limits and a projective class, to an abelian cat. This encompasses several other notions.
http://www.ncatlab.org/nlab/show/satellite
http://ncatlab.org/nlab/show/derived+functor+on+a+derived+category
Def: A left Ken Brown functor is a functor which carries trivial cofibs between cofibrant objects to weak equivalences. I think it is true that a left KB functor admits an absolute total left derived functor (Maltsiniotis lectures in Seville). Also, consider a composition of a functor
 followed by another functor
followed by another functor 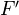 . Assume both are KB, and that
. Assume both are KB, and that  takes cofibrant objects to cofibrant objects. Then
takes cofibrant objects to cofibrant objects. Then 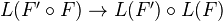 is an iso.<]]>
is an iso.<]]>- Derived loop spaceWrite comment View comments
Toen: Algebres simplicicales etc, file Toen web prepr rhamloop.pdf. Comparison between functions on derived loop spaces and de Rham theory. Take a smooth k-algebra, k aof char zero. Then (roughly) the de Rham algebra of A and the simplical algebra
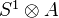 determine each other (functorial equivalence). Consequence: For a smooth k-scheme
determine each other (functorial equivalence). Consequence: For a smooth k-scheme  , the algebraic de Rham cohomology is identified with
, the algebraic de Rham cohomology is identified with 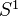 -equivariant functions on the derived loop space of
-equivariant functions on the derived loop space of  . Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]>
. Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]>- Derived stackWrite comment View comments
Toen remark in Seville: The inclusion from stacks to derived stacks is a full embedding which admits a right adjoint, but does NOT commute with holim. That's why we need derived stacks to get "correct" limits.
arXiv:1101.3300 Constructing derived moduli stacks from arXiv Front: math.AG by J. P. Pridham We introduce frameworks for constructing global derived moduli stacks associated to a broad range of problems, bridging the gap between the concrete and abstract conceptions of derived moduli. Our three approaches are via differential graded Lie algebras, via cosimplicial groups, and via quasi-comonoids, each more general than the last. Explicit examples of derived moduli problems addressed here are finite schemes, polarised projective schemes, torsors, coherent sheaves, and finite group schemes.
arXiv:1102.1150 Derived algebraic geometry, determinants of perfect complexes, and applications to obstruction theories for maps and complexes from arXiv Front: math.KT by Timo Schürg, Bertrand Toën, Gabriele Vezzosi We show how a quasi-smooth derived enhancement of a Deligne-Mumford stack naturally endows the stack with a functorial perfect obstruction theory in the sense of Behrend-Fantechi. This result is then applied to moduli of maps and perfect complexes on a smooth complex projective variety. For moduli of maps, for X=S a smooth algebraic K3-surface, $g\geq 0$, and $\beta \neq 0$ a curve class, we construct a derived stack whose truncation is the usual stack of pointed stable maps from curves of genus g to S hitting the class $\beta$, and such that the inclusion of the truncation into the full derived stack induces on the stack a perfect obstruction theory whose tangent and obstruction spaces coincide with the corresponding reduced spaces of Okounkov-Maulik-Pandharipande-Thomas. The approach we present here uses derived algebraic geometry and yields not only a full rigorous proof of the existence of a reduced obstruction theory - not relying on any result on semiregularity maps - but also a new global geometric interpretation. For moduli of complexes, we construct a map from the derived stack of stable embeddings of curves (into a smooth complex projective variety X) to the derived stack of simple perfect complexes on X with vanishing negative Ext's, and show how this map induces a morphism of the correponding obstruction theories, in the case X is a Calabi-Yau threefold. We relate this result to the conjectural comparison between Gromov-Witten snd Donaldson-Thomas invariants. An important ingredient of our construction is a perfect determinant map from the derived stack of perfect complexes to the derived stack of line bundles whose tangent morphism is, pointwise, Illusie's trace map for perfect complexes.
<]]>- DescentWrite comment View comments
nLab entry, check this and also this
Conrad: Cohomological descent (hypercover.pdf)
http://ncatlab.org/nlab/show/descent+for+simplicial+presheaves
http://ncatlab.org/nlab/show/hypercompletion
http://ncatlab.org/nlab/show/Carlos+Simpson
Descent: See Borceaux vol2 chapter for a categorical viewpoint.
Déglise uses something for rigid cohomology
Guillen and Navarro Aznar uses something called a "descent category" in their "extension" paper.
Friedlander, Walker: Semitopological K-theory of real varieties. Proves Nisnevich descent! Review says that the corresponding fact for alg K-th was proved by Thomason.
Giraud: Technique de descente, 1964.
R. Street, Descent, Oberwolfach preprint, mentioned by Toby Bartels at nLab
rectified infinity-stack at nLab
A must-read for descent: Toen: Thm de RR pour les champs de DM. File Toen web publ rrchamp.pdf. Discusses K-theory and RR for DM stacks, but also various notions of descent, including basic stuff on simplicial presheaves, homological descent, and etale descent.
For the notion of descent data, see Toen course in cours folder under Toen, chapter 5. Also in Vistoli maybe.
Possibly interesting: Descent theory for derived categories. Alexei D Elagin 2009 Russ. Math. Surv. 64 748-749
Email from Peter, July 09:
I stick to the slogan: descent means glueing is respected... what ever that means. So it is some sheaf condition. Somehow descent for a functor (aka this functor being a (higher) stack) means, after Toen and many others, that F(X) = holim(cech simpl. object of any (hyper)covering of X). See the notes, hopefully... For seeing how Galois descent is an instance of that I found the relevant chapter in Waterhouse illuminating - I don't claim I understood it but it seems to put one on the right track.
Brown rep.: After Neeman's article ("Brown rep. and Grothendieck duality via Bousfield's techniques") Brown rep. holds for compactly generated triangulated categories which SH(Z) should be; I think connected schemes are generators for sPre(Sm/k) - every presheaf is a colim of Homs, i.e. of schemes (and non-connected schemes are coproducts of connected sch.s), every simplicial set is a colim of its simplices, now one would have to combine these, maybe one needs additionally the constant sheaves with value
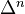 as generators (?).
Then hence they would be generating for SH(Z) (localizing only makes
them a "bigger" subset of all objects). Intuition says that these are
compact in SH(Z) but I know no proof.
as generators (?).
Then hence they would be generating for SH(Z) (localizing only makes
them a "bigger" subset of all objects). Intuition says that these are
compact in SH(Z) but I know no proof.One can shift the difficulty thus: Neeman proves in his book that Brown rep. holds for "well-generated" categories (see Krause for a definition) and Rosicky says in the introduction to his article that he shows that combinatorial model cats give well-generated triangulated cats. Now here the Brown rep. theorem is probably more difficult but it is easy to see that SH(Z) falls under its scope. Roughly: Combinatorial = accessible i.e. everything is filtered colim of presentable objects, i.e. objects s.t. Hom out of them commutes with filtered colims. This is clearly the case for sPre(C), C any cat: It is a functor category, namely
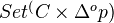 and in such
everythin is filtered colim of representables...
and in such
everythin is filtered colim of representables...
A bibliography:
- J. Bénabou and J. Roubaud paper Monades et Descente jour Comptes Rendus Acad. Sc. Paris 270, série A \\\\\\\\pages 96--98 \\\\\\\\yr 1970 \\\\\\\\lang French
- R. Betti \\\\\\\\paper Adjointness in descent theory \\\\\\\\jour J. Pure Appl. Algebra 116, No.1-3 \\\\\\\\pages 41--47 \\\\\\\\yr 1997
- I. Bucur \\\\\\\\book Selected Topics in Algebra \\\\\\\\publaddr D. Reidel Publishing Company (Dordrecht, Boston, Lancaster) \\\\\\\\yr 1984
- J. Duskin\\\\\\\\paper An Outline of a Theory of Higher Dimensional Descent \\\\\\\\jour Bull. Soc. Math. de Belgique (Serie A) \\\\\\\\vol Tome XLI Fasc. 2 \\\\\\\\pages 249--277 \\\\\\\\yr 1989
- Duskin \\\\\\\\paper The Theory of Descent \\\\\\\\paperinfo (xx+230 pp.) unpublished appendix
- Duskin \\\\\\\\talk Triples and Descent preprint of talks given at Oberwolfach \\\\\\\\yr Sep. 17-23 1995.
- A. Grothendieck\\\\\\\\paper Technique de Déscente et Théoréms d\\\\\\\\'Existence en Géométrie Algébrique. Généralités. Déscente par Morphisms Fidélment Plat \\\\\\\\inbook Séminaire Bourbaki, $12^e$ no.190 \\\\\\\\yr 59--60 \\\\\\\\lang French
- \\\\\\\\bysame \\\\\\\\paper Categories Fibrées et Déscente,Déscente Fidelment plat, and Déscente des Morphisms etales \\\\\\\\inbook S.G.A. 1 exposé VI,VIII and IX,respectively Lec. Notes in Math. \\\\\\\\#224 \\\\\\\\yr 1971\\\\\\\\lang French
- G. Janelidze and W. Tholen \\\\\\\\paper Facets of descent. I. \\\\\\\\jour [J] Appl. Categ. Struct. 2, No.3, \\\\\\\\pages 245--281 \\\\\\\\yr 1994.
- G. Janelidze and W. Tholen \\\\\\\\paper Facets of descent. II. \\\\\\\\jour [J] Appl. Categ. Struct. 5, No.3, \\\\\\\\pages 229--248 \\\\\\\\yr 1997
- A. Joyal and M. Tierney \\\\\\\\paper An Extension of the Galois Theory of Grothendieck \\\\\\\\jour Memoirs Amer. Math. Soc. 309 \\\\\\\\yr 1984
- M .A. Knus, and M. Ojanguren \\\\\\\\book Théorie de la Dé scente et Algébras de Azumaya \\\\\\\\bookinfo Lec. Notes in Math. \\\\\\\\#389 \\\\\\\\yr 1974 \\\\\\\\lang French
- W. Lawvere \\\\\\\\book Theory of Categories over a Base Topos \\\\\\\\publaddr Mimeographed notes, Perugia \\\\\\\\yr 1972--73 \\\\\\\\pages 30 and 70
- I. Moerdijk \\\\\\\\paper Descent Theory for Toposes \\\\\\\\jour Bull. Soc. Math. de Belgique (Series A)\\\\\\\\vol Tome XLI Fasc. 2 \\\\\\\\pages 373--391 \\\\\\\\yr 1989
- M. Sobraland W. Tholen \\\\\\\\paper Effective Descent Morphisms and Effective Equivalence Relations \\\\\\\\inbook Can. Math. Soc. Conference Proceedings \\\\\\\\vol 13 \\\\\\\\pages 421--433 \\\\\\\\yr 1992
- W.C. Waterhouse \\\\\\\\book Introduction to Affine Group Schemes \\\\\\\\bookinfo Graduate texts in math. \\\\\\\\#66 \\\\\\\\yr 1979 \\\\\\\\publaddr Springer-Verlag (New York)
<]]>- Descent IIWrite comment View comments
http://mathoverflow.net/questions/22032/what-is-descent-theory
http://www.ncatlab.org/nlab/show/cohomological+descent
Menini and Dragos on Descent theory and Amitsur cohomology of triples, with a nice general introduction on descent theory in the algebraic setting.
arXiv:1103.3135 Cohomological descent theory for a morphism of stacks and for equivariant derived categories from arXiv Front: math.AG by Alexey Elagin In the paper we answer the following question: for a morphism of varieties (or, more generally, stacks), when the derived category of the base can be recovered from the derived category of the covering variety by means of descent theory? As a corollary, we show that for an action of a reductive group on a scheme, the derived category of equivariant sheaves is equivalent to the category of objects, equipped with an action of the group, in the ordinary derived category.
arXiv:1001.1556 A general framework for homotopic descent and codescent from arXiv Front: math.KT by Kathryn Hess In this paper we elaborate a general homotopy-theoretic framework in which to study problems of descent and completion and of their duals, codescent and cocompletion. Our approach to homotopic (co)descent and to derived (co)completion can be viewed as $\infty$-category-theoretic, as our framework is constructed in the universe of simplicially enriched categories, which are a model for $(\infty, 1)$-categories.
We provide general criteria, reminiscent of Mandell's theorem on $E_{\infty}$-algebra models of $p$-complete spaces, under which homotopic (co)descent is satisfied. Furthermore, we construct general descent and codescent spectral sequences, which we interpret in terms of derived (co)completion and homotopic (co)descent.We show that a number of very well-known spectral sequences, such as the unstable and stable Adams spectral sequences, the Adams-Novikov spectral sequence and the descent spectral sequence of a map, are examples of general (co)descent spectral sequences. There is also a close relationship between the Lichtenbaum-Quillen conjecture and homotopic descent along the Dwyer-Friedlander map from algebraic K-theory to étale K-theory. Moreover, there are intriguing analogies between derived cocompletion (respectively, completion) and homotopy left (respectively, right) Kan extensions and their associated assembly (respectively, coassembly) maps.arXiv:0911.3554 Flat descent for Artin n-stacks from arXiv Front: math.CT by B. Toen We prove two flat descent statements for Artin n-stacks. We first show that an n-stack for the etale topology which is an Artin n-stack in the sense of HAGII, is also an n-stack for the fppf topology. Moreover, an n-stack for the fppf topology which possess a fppf n-atlas is an Artin n-stack (i.e. possesses a smooth n-atlas). We deduce from these results some comparison statements between fppf and etale (non-ablelian) cohomolgies. This paper is written in the setting of derived algebraic geometry and its results are also valid for derived Artin n-stacks.
arXiv:0808.3684 (Co)Simplicial Descent Categories from arXiv Front: math.AT by Beatriz Rodriguez Gonzalez Let D be a category and E a class of morphisms in D. In this paper we study the question of how to transfer homotopic structure from the category of simplicial objects in D, sD, to D through a `good' functor s : sD --> D, which we call simple functor. For instance, the homotopy colimit in a Quillen simplicial model category is a good simple functor. As a remarkable example outside the setting of Quillen models we include Deligne's simple of mixed Hodge complexes. We prove here that the simple functor induces an equivalence on the corresponding localized categories. We also show that sD is in a natural way a Brown category of cofibrant objects. We use these facts to produce cofiber sequences on the localized category of D by E, which give rise to a natural Verdier triangulated structure in the stable case.
http://mathoverflow.net/questions/72140/schemes-do-not-form-a-stack-in-the-etale-topology
http://mathoverflow.net/questions/6979/what-is-etale-descent
http://mathoverflow.net/questions/37970/do-coequalizers-in-ringspc-automatically-lead-to-descent
There is some descent stuff in Waterhouse, with group schemes in mind. In alg gps and gp schemes folder.
http://www.ncatlab.org/nlab/show/descent+in+noncommutative+algebraic+geometry
nlab: monadic descent
<]]>- Descent IIIWrite comment View comments
arXiv:1206.3439 Pure morphisms are effective for modules from arXiv Front: math.CT by Bachuki Mesablishvili Yet another proof of the result asserting that a morphism of commutative rings is an effective descent morphism for modules if and only if it is pure is given. Moreover, it is shown that this result cannot be derived from Moerdijk's descent criterion.
http://mathoverflow.net/questions/34904/when-does-a-vector-bundle-descent
On proper descent for crystalline cohomology (fails): http://math.columbia.edu/~dejong/wordpress/?p=2201
arXiv:1211.1813 Pro excision and h-descent for K-theory fra arXiv Front: math.AG av Matthew Morrow In this paper it is proved that K-theory (and Hochschild and cyclic homology) satisfies pro versions of both excision for ideals (of commutative Noetherian rings) and descent in the h-topology in characteristic zero; this is achieved by passing to the limit over all infinitesimal thickenings of the ideal or exceptional fibre in question.
<]]>- Descent spectral sequenceWrite comment View comments
- <]]>
- Dessins d'enfantsWrite comment View comments
http://mathoverflow.net/questions/53362/what-do-dessins-tell-us-about-the-absolute-galois-group
See the final chapter of Douady: Algebre et th galoisiennes, in folder AG/Various
http://mathoverflow.net/questions/1909/what-are-dessins-denfants
<]]>- DeterminantsWrite comment View comments
Knudsen: Determinant of cohomology. In Homol alg folder
Something in the work of Faltings/Gillet/Soulé I think???
arXiv:1006.5399 On determinant functors and $K$-theory from arXiv Front: math.CT by Fernando Muro, Andrew Tonks, Malte Witte In this paper we introduce a new approach to determinant functors which allows us to extend Deligne's determinant functors for exact categories to Waldhausen categories, (strongly) triangulated categories, and derivators. We construct universal determinant functors in all cases by original methods which are interesting even for the known cases. Moreover, we show that the target of each universal determinant functor computes the corresponding $K$-theory in dimensions $0$ and $1$. As applications, we answer open questions by Maltsiniotis and Neeman on the $K$-theory of (strongly) triangulated categories and a question of Grothendieck to Knudsen on determinant functors. We also prove additivity and localization theorems for low-dimensional $K$-theory and obtain generators and (some) relations for various $K_{1}$-groups.
<]]>- DevissageWrite comment View comments
- <]]>
- DG stuffWrite comment View comments
Why is DG stuff coming up everywhere?
http://ncatlab.org/nlab/show/differential+graded+objects+-+contents
http://ncatlab.org/nlab/show/motives+and+dg-categories
http://ncatlab.org/nlab/show/differential+graded+vector+space
http://mathoverflow.net/questions/37202/derived-algebraic-geometry-via-dg-rings
Lunts and Orlov: Uniqueness of enhancement for triang cats arXiv
For model structure on DG-algebras, see Gelfand and Manin: Methods of homological algebra, Chapter 5.
Hesselholt in K-theory handbook, p. 81: The derived category of abelian groups is a triangulated category and a smmetric monoidal category. A monoid for the tensor product is called a differential graded ring. If
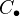 is a simplicial abelian group, write
is a simplicial abelian group, write 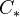 for the associated chain complex. If
for the associated chain complex. If 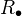 is a simplicial ring, then
is a simplicial ring, then 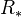 is a DG ring (details spelled out...). If
is a DG ring (details spelled out...). If  is a commutative ring, then
is a commutative ring, then 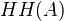 is a simplicial ring.
is a simplicial ring.I think this is what I thinking of: http://www.math.univ-toulouse.fr/~toen/swisk.pdf but I haven't actually read them myself. There might also be something else by Toen on his webpage.
Also, here is a thesis which looks good: http://people.math.jussieu.fr/~keller/TabuadaThese.pdf
Things by Keller: http://front.math.ucdavis.edu/0601.5185 and also http://www.numdam.org/item?id=ASENS_1994_4_27_1_63_0 both look useful to me.
Maybe there is something useful in Neeman's chapter in the K-theory handbook vol 2, which might possibly be the same as this link: http://wwwmaths.anu.edu.au/~neeman/preprints/author.ps
nLab: dg-algebra and dg-category
<]]>- DG-algebraWrite comment View comments
Toen: Anneaux de definition etc, file Toen web publ defdgalg.pdf, on rings of definition for smooth and proper dg-algebras. An application is the possibility of arguments passing to char p, and in particular study of Hodge to de Rham degeneration. Ref to Kaledin: Noncommutative Hodge-to-de-Rham deg via etc.
Toen: Finitude homotopique etc. File Toen web publ dgalgsat.pdf.
http://ncatlab.org/nlab/show/differential+graded+algebra
http://www.ncatlab.org/nlab/show/differential+graded+coalgebra
http://ncatlab.org/nlab/show/differential+graded+Hopf+algebra
http://www.ncatlab.org/nlab/show/model+structure+on+dg-algebras
<]]>- DG-categoryWrite comment View comments
[Ke3] B. Keller, On differential graded categories, preprint (available on Keller's webpage).
Toen: Lecture on DG-categories. File Toen web unpubl swisk.pdf. Treats basic theory, localization, relation to model cats, functorial cones, K-theory and Hochschild cohomology, and descent problems.
Toen: The homotopy theory of dg-cats and derived Morita theory. File Toen web publ mapdgcat.pdf.
Toen and Vaquie: Moduli of objects in dg-cats: Discusses triang cats with some finiteness assumptions, admitting a dg-enhancement. File Toen web publ ttt.pdf.
http://ncatlab.org/nlab/show/dg-category
arXiv:0908.4187 Uniqueness of enhancement for triangulated categories from arXiv Front: math.AG by Valery A. Lunts, Dmitri O. Orlov The paper contains general results on the uniqueness of a DG enhancement for triangulated categories. As a consequence we obtain such uniqueness for the unbounded categories of quasi-coherent sheaves, for the triangulated categories of perfect complexes, and for the bounded derived categories of coherent sheaves on quasi-projective schemes. If a scheme is projective then we also prove a strong uniqueness for the triangulated category of perfect complexes and for the bounded derived categories of coherent sheaves. These results directly imply that fully faithful functors from the bounded derived categories of coherent sheaves and the triangulated categories of perfect complexes on projective schemes can be represented by objects on the product.
<]]>- DG-schemeWrite comment View comments
Toen and Vezzosi: Algebraic geometry over model categories. Early paper, looks very nice! Applications to interpreting DG-schemes, and to defining etale K-theory of E-infty algebras. Expectation to extend the classical work for E-infty algebras to the more general setting of AG over a model cat, for the following concepts: tangent Lie algebra, cotangent complex, Hochschild cohomology, K-theory, A-Q cohomology. Would like to do AG over a symmetric monoidal infty-cat, need strictification results. An E-infty alg should be a monoid in a SM infty-cat. Pp 34: Short nice review of operads and E-infty stuff.
<]]>- DGAWrite comment View comments
J.F. Jardine, "A closed model structure for differential graded algebras", Cyclic Cohomology and Noncommutative Geometry, Fields Institute Communications, Vol. 17, AMS (1997), 55-58.
Ivorra gave a talk in Oberw July 09 in which he defined an A-infty algebra as something with an infinite sequenec of maps, and said that if you take all these except the first three to be zero, you recover the def of a DGA. Hence I guess CDGAs should correspond to E-infty algebras, and sheaves of cDGAs to blabla.
<]]>- DGLAWrite comment View comments
http://ncatlab.org/nlab/show/differential+graded+Lie+algebra
http://mathoverflow.net/questions/385/deformation-theory-and-differential-graded-lie-algebras
<]]>- DieudonneWrite comment View comments
There exists collected works
<]]>- Dieudonne theoryWrite comment View comments
Starting point: Classification of formal groups over fields of char p. See Breen survey in Asterisque 63 (1978) if needed.
http://mathoverflow.net/questions/96507/reference-for-dieudonne-modules
<]]>- Differential formsWrite comment View comments
See diff forms folder
http://ncatlab.org/nlab/show/differential+form
http://nlab.mathforge.org/nlab/show/K%C3%A4hler+differential
<]]>- Differential geometryWrite comment View comments
Lots of exciting books in Diff geom folder
Very basic but very good notes: David Mond, in Geometry-Various folder. These are from a course, which also used Morita: Geometry of differential forms (ch 5 in particular), and Madsen-Tornehave: From calculus to cohomology.
More books on library.nu, including Schaum's outline and Spivak's series.
Surveys in differential geometry, a supplement to the Journal of Diff geom. This might be a good way to get into current diff geom. A number of volumes
<]]>- Differential operatorWrite comment View comments
Johannes once explained something nice about these, maybe in the copy of his papers.
A book by Snaith: An introduction to global analysis
<]]>- Differential topologyWrite comment View comments
- <]]>
- DimensionWrite comment View comments
There are many different notions of dimension. I think Manin has a survey paper. Artin-Stafford use Gelfand-Kirillov dimension of an algebra in their Inventiones paper.
Dobbs LNM0147: Cech cohomological dimension for comm rings.
http://ncatlab.org/nlab/show/cohomological+dimension
http://ncatlab.org/nlab/show/homotopy+dimension
<]]>- Diophantine approximationWrite comment View comments
[arXiv:0908.3973] Report on some recent advances in Diophantine approximation from arXiv Front: math.NT by Michel Waldschmidt A basic question of Diophantine approximation, which is the first issue we discuss, is to investigate the rational approximations to a single real number. Next, we consider the algebraic or polynomial approximations to a single complex number, as well as the simultaneous approximation of powers of a real number by rational numbers with the same denominator. Finally we study generalisations of these questions to higher dimensions. Several recent advances have been made by B. Adamczewski, Y. Bugeaud, S. Fischler, M. Laurent, T. Rivoal, D. Roy and W.M. Schmidt, among others. We review some of these works.
<]]>- Diophantine geometryWrite comment View comments
arXiv:1210.0304 Diophantine Geometry and Analytic Spaces fra arXiv Front: math.AG av Antoine Chambert-Loir This text is the write-up of a talk at the Bellairs Workshop in Number Theory on Tropical and Non-Archimedean Geometry that took place at the Bellairs Research Institute, Barbados, in May 2011. The goal of this text is to present recent work by in Diophantine Geometry over function fields due to Gubler and Yamaki, where analytic geometry in the sense of Berkovich plays a significant place. I also give an introduction to basic concepts and notions on Diophantine Geometry, such as heights, the Manin-Mumford conjecture, the Bogomolov conjecture, and its proof by Ullmo and Zhang.
<]]>- DoctrineWrite comment View comments
- <]]>
- DokchitserWrite comment View comments
- <]]>
- Dold-Kan correspondenceWrite comment View comments
An adjoint equivalence
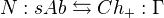 . The Eilenberg-MacLane space
. The Eilenberg-MacLane space 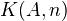 can be defined as
can be defined as 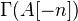 where
where 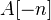 is
is  placed in degree
placed in degree  .
.Details are written out in Weibel (chapter 8?) and also in Goerss-Schemmerhorn, section 4 and p. 16. One way of thinking of this is that since simplicial groups are fibrant as simplicial sets, their homotopy groups can be computed combinatorially, and the recipe for doing this is given by the Dold-Kan correspondence.
For details on the model cat of simplicial abelian groups and the Dold-Kan corr, see Goerss-Jardine section III.2. Consequences include the description of cohomology as a Hom into an EM space, and the fact that every simplicial abelian group is non-canonically homotopy equivalent to a product of EM spaces.
Stable version in Tierney LNM0087.
Moore complex in nlab
http://ncatlab.org/nlab/show/Dold-Kan+correspondence
A preprint of Shoikhet related to monoidal properties of Dold-Kan: http://front.math.ucdavis.edu/1109.5441
http://ncatlab.org/nlab/show/monoidal+Dold-Kan+correspondence
I mentioned some more general versions of DK in the Homotopical cats blog post I think, with refs.
Dendroidal Dold-Kan correspondence
D-K corr holds in general for simplicial objects in a semiabelian category, see remark at nLab
http://mathoverflow.net/questions/32755/is-there-any-generalization-of-the-dold-kan-correspondence
arXiv:1109.5441 A bialgebra axiom and the Dold-Kan correspondence from arXiv Front: math.KT by Boris Shoikhet We introduce a bialgebra axiom for a pair $(c,\ell)$ of a colax-monoidal and a lax-monoidal structures on a functor $F\colon \mathscr{M}1\to \mathscr{M}2$ between two (strict) symmetric monoidal categories. This axiom can be regarded as a weakening of the property of $F$ to be a strict symmetric monoidal functor. We show that this axiom transforms well when passing to the adjoint functor or to the categories of monoids. Rather unexpectedly, this axiom holds for the Alexander-Whitney colax-monoidal and the Eilenberg-MacLane lax-monoidal structures on the normalized chain complex functor in the Dold-Kan correspondence. This fact, proven in Section 2, opens up a way for many applications, which we will consider in our sequel paper(s).
<]]>- Dold-Thom theoremWrite comment View comments
- <]]>
- Donaldson-Thomas invariantsWrite comment View comments
Joyce survey on generalized Donaldson-Thomas invariants http://arxiv.org/abs/0910.0105
arXiv:0910.4315 Motivic Donaldson-Thomas invariants: summary of results from arXiv Front: math.AG by Maxim Kontsevich, Yan Soibelman This is a short summary of main results of our paper arXiv:0811.2435 where the concept of motivic Donaldson-Thomas invariant was introduced. It also contains a discussion of some open questions from the loc.cit., in particular, the geometry related to the split attractor flow.
http://ncatlab.org/nlab/show/Donaldson-Thomas+invariant
arXiv:1103.4229 Stability conditions and curve counting invariants on Calabi-Yau 3-folds from arXiv Front: math.AG by Yukinobu Toda The purpose of this paper is twofold: first we give a survey on the recent developments of curve counting invariants on Calabi-Yau 3-folds, e.g. Gromov-Witten theory, Donaldson-Thomas theory and Pandharipande-Thomas theory. Next we focus on the proof of the rationality conjecture of the generating series of PT invariants, and discuss its conjectural Gopakumar-Vafa form.
[arXiv:0910.0105] Generalized Donaldson-Thomas invariants from arXiv Front: math.AG by Dominic Joyce This is a survey of the book arXiv:0810.5645 with Yinan Song. Let X be a Calabi-Yau 3-fold over C. The Donaldson-Thomas invariants of X are integers DT^a(t) which count stable sheaves with Chern character a on X, with respect to a Gieseker stability condition t. They are defined only for Chern characters a for which there are no strictly semistable sheaves on X. They have the good property that they are unchanged under deformations of X. Their behaviour under change of stability condition t was not understood until now.
We discuss "generalized Donaldson-Thomas invariants" \bar{DT}^a(t). These are rational numbers, defined for all Chern characters a, and are equal to DT^a(t) if there are no strictly semistable sheaves in class a. They are deformation-invariant, and have a known transformation law under change of stability condition. We conjecture they can be written in terms of integral "BPS invariants" \hat{DT}^a(t) when the stability condition t is "generic".We extend the theory to abelian categories of representations of a quiver with relations coming from a superpotential, and connect our ideas with Szendroi's "noncommutative Donaldson-Thomas invariants" and work by Reineke and others. There is significant overlap between arXiv:0810.5645 and the independent paper arXiv:0811.2435 by Kontsevich and Soibelman.Vittoria Bussi (Oxford): Donaldson–Thomas theory: generalizations and related conjectures. Joyce-style abstract: Generalized Donaldson–Thomas invariants defined by Joyce and Song are rational numbers which "count" both τ-stable and τ-semistable coherent sheaves with Chern character α on a Calabi–Yau 3-fold X, where τ denotes Gieseker stability for some ample line bundle on X. These invariants are defined for all classes α, and are equal to the classical DT defined by Thomas when it is defined. They are unchanged under deformations of X, and transform by a wall-crossing formula under change of stability condition τ. Joyce and Song use gauge theory and transcendental complex analytic methods, so that the theory of generalized Donaldson–Thomas invariants is valid only in the complex case. This also forces them to put constraints on the Calabi–Yau 3-fold they can define generalized Donaldson–Thomas invariants for. This seminar will propose a new algebraic method extending the theory to algebraically closed fields K of characteristic zero. We will describe the local structure of the moduli stack M of coherent sheaves on X, showing that an atlas for M may be written locally as the zero locus of an almost closed 1-form defined on an etale neighborhood in the tangent space of M and use this to deduce identities on the Behrend function. This last statement has yet a gap in its proof, which we are going to fix soon. This will yield also the extension of generalized Donaldson–Thomas theory to compactly supported coherent sheaves on noncompact quasi-projective Calabi–Yau 3-folds. A similar argument, adapted to complexes of sheaves, should yield also to the validity of generalized DT invariants theory in the derived categorical framework, extending an announced result by Behrend and Getzler, and proving an important conjecture by Toda. Finally we depict several ideas on further developments of in the DT theory, suggested by our strategy, in the direction of motivic and categorified DT invariants in the sense of Kontsevich and Soibelman.
<]]>- DrinfeldWrite comment View comments
- <]]>
- DualityWrite comment View comments
Is there a direct link between Poincaré duality and Langlands duality, since both are reflected in functional equations?
http://mathoverflow.net/questions/73711/the-concept-of-duality
Functional analysis on the eve of the 21st century Contains article by Kapranov: Analogies between the Langlands Correspondence and Topological QFT. Follow-up here at MO.
Alex S mentioned some very general form of Poincaré duality
Gross-Hopkins duality mentioned by Behrens here
Hartshorne: Residues and duality, LNM0020.
Something about string theory and a very general form of Poincaré duality
An interesting framework by Greenlees, Dwyer, Iyengar
Duality for abelian schemes: See Oort: LNM0015.
Altman and Kleiman LNM0146 Intro to Grothendieck duality. Looks very readable.
Preprint in progress of Rognes: Topological arithmetic duality
Scholbach thesis hints at duality underlying L-function stuff.
Saito: Cohomological Hasse principle for a threefold over a finite field review. Uses "arithmetic Poincaré duality", according to the review.
http://nlab.mathforge.org/nlab/show/dualizable+object
Minhyong Kim gave a talk in Cambridge in Feb 2011 called "Remarks on non-abelian duality"
<]]>- DuggerWrite comment View comments
Web page with lots of excellent material including "Navigating the motivic world", and stuff on simplicial sheaves
<]]>- Durov geometryWrite comment View comments
arXiv:1207.3890 On the algebraic K-theory of Spec Z^N fra arXiv Front: math.KT av Stella Anevski In his thesis, N. Durov develops a theory of algebraic geometry in which schemes are locally determined by commutative algebraic monads. In this setting, one is able to construct the Arakelov geometric compactification of the spectrum of the ring of integers in a purely algebraic fashion. This object arises as the limit of a certain projective system of generalized schemes. We study the constituents of this projective system, and compute their algebraic K-theory.
<]]>- DwyerWrite comment View comments
- <]]>
- DégliseWrite comment View comments
- <]]>