Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- E-infinity algebraWrite comment View comments
http://mathoverflow.net/questions/36444/definition-of-an-e-infinity-algebra
Over a ring which is not a field, must work with E-infinity algebras instead of CDGAs. See Toen Essen talk p 30 for a discussion of viewing this setup in terms of model sites, and the right notion of all the usual topologies on schemes in the homotopical setting.
Toen and Vezzosi: Algebraic geometry over model categories. Early paper, looks very nice! Applications to interpreting DG-schemes, and to defining etale K-theory of E-infty algebras. Expectation to extend the classical work for E-infty algebras to the more general setting of AG over a model cat, for the following concepts: tangent Lie algebra, cotangent complex, Hochschild cohomology, K-theory, A-Q cohomology. Would like to do AG over a symmetric monoidal infty-cat, need strictification results. An E-infty alg should be a monoid in a SM infty-cat. Pp 34: Short nice review of operads and E-infty stuff.
http://mathoverflow.net/questions/77350/new-model-structure-on-e-infty-algebras
Cisinski email to Jakob (Feb 2011): une structure d'algèbre sur l'opérade E-infini. De manière imagée, cela veut dire un produit qui soit unitaire à homotopie près, associatif à homotopie près, et commutatif à homotopie près, mais avec beaucoup plus de structures (assez pour encoder tout cela pour les opérations sur n variables, et pour dire que les homotopies en question sont elles mêmes uniques à homotopie près...). Ce point de vue des opérades est un peu plus lourd que celui des monoïdes commutatifs, mais a le mérite d'être très robuste (dans la nature, il y a beaucoup plus d'algèbres sur l'opérade E-infini que de monoïdes commutatifs). La bonne nouvelle, c'est que, dans le monde des complexes d'espaces vectoriels sur un corps de caractéristique nulle, toute algèbre sur l'opérade E-infini est quasi-isomorphe à une k-algèbre différentielles graduée commutative; la manière précise d'énoncer cela est: pour tout corps de caractéristique nulle k, il existe une équivalence de Quillen entre la catégorie des algèbres sur l'opérade E-infini dans la catégorie des (faisceaux de) complexes de k-espaces vectoriels et la catégorie des monoïdes commutatifs dans la catégorie des (faisceaux de) complexes de k-espaces vectoriels (aussi connus sous le nom de k-algèbres différentielles graduées commutatives).
http://mathoverflow.net/questions/46384/definition-of-an-e-n-algebra
arXiv:1109.1598 Algebraic theories, span diagrams and commutative monoids in homotopy theory from arXiv Front: math.CT by James Cranch We adapt the notion of an algebraic theory to work in the setting of quasicategories developed recently by Joyal and Lurie. We develop the general theory at some length.
We study one extended example in detail: the theory of commutative monoids (which turns out to be essentially just a 2-category). This gives a straightforward, combinatorially explicit, and instructive notion of a commutative monoid. We prove that this definition is equivalent (in appropriate senses) both to the classical concept of an E-infinity monoid and to Lurie's concept of a commutative algebra object.<]]>- E-infinity ringWrite comment View comments
http://www.ncatlab.org/nlab/show/E-infinity-ring
nLab: E_k operad
http://www.ncatlab.org/nlab/show/Barratt-Eccles+operad
See this review for a remark about the interpretation of E-infinity for non-CW homotopy types, e.g. related to profinite groups.
E-infinity stuff. LNM0577: E-infinity ring spaces and E-infty ring spectra
arXiv:0910.3566 H-infinity is not E-infinity from arXiv Front: math.AT by Justin Noel We provide an example of a spectrum with an H-infty structure which does not rigidify to an E3 structure. It follows that not every H-infinity ring spectrum comes from an underlying E-infinity ring spectrum. After comparing definitions, we obtain this example by applying Sigma^\infty+ to the counterexample to the transfer conjecture constructed by Kraines and Lada.
arXiv:1103.2764 Diagram spaces and symmetric spectra from arXiv Front: math.AT by Steffen Sagave, Christian Schlichtkrull We present a general homotopical analysis of structured diagram spaces and discuss the relation to symmetric spectra. The main motivating examples are the I-spaces, which are diagrams indexed by finite sets and injections, and J-spaces, which are diagrams indexed by the Grayson-Quillen construction on the category of finite sets and bijections. We show that the category of I-spaces provides a convenient model for the homotopy category of spaces in which every E-infinity space can be rectified to a strictly commutative monoid. Similarly, the commutative monoids in the category of J-spaces model graded E-infinity spaces. Using the theory of J-spaces we introduce the graded units of a symmetric ring spectrum. The graded units detect periodicity phenomena in stable homotopy and we show how this can be applied to the theory of topological logarithmic structures.
<]]>- Effective epimorphismWrite comment View comments
See Tamme p. 25-26.
<]]>- EhresmannWrite comment View comments
Oeuvres, many volumes, at least up to IV-2.
<]]>- Eichler-Shimura theoryWrite comment View comments
A chapter in Knapp: Elliptic curves
Probably references in Diamond-Shurman
<]]>- EigencurveWrite comment View comments
Coleman, R.; Mazur, B. The eigencurve. Galois representations in arithmetic algebraic geometry (Durham, 1996), 1--113, London Math. Soc. Lecture Note Ser., 254, Cambridge Univ. Press, Cambridge, 1998
A seminar page from Essen with lots of references.
http://mathoverflow.net/questions/75144/global-applications-of-eigenvarieties
<]]>- EilenbergWrite comment View comments
- <]]>
- Eilenberg-MacLane spaceWrite comment View comments
See also May or any proper book on algebraic topology
http://mathoverflow.net/questions/61545/low-degree-cohomology-of-eilenberg-maclane-space-kg-2
http://mathoverflow.net/questions/40553/loopspace-of-an-eilenberg-maclane-space-kg-n
<]]>- Eilenberg-Zilber theoremWrite comment View comments
See Jardine-Goerss chapter IV. The theorem says roughly that the two ways of extracting a chain complex from a bisimplicial abelian group are naturally chain homotopy equivalent. (Total complex vs the chain complex associated to the diagonal simplicial ab gp).
<]]>- Eisenstein seriesWrite comment View comments
- <]]>
- EkedahlWrite comment View comments
- <]]>
- Elliptic curvesWrite comment View comments
http://mathoverflow.net/questions/2022/definition-and-meaning-of-the-conductor-of-an-elliptic-curve
[arXiv:1207.0287] On the Selmer groups and Mordell-Weil groups of elliptic curves $ y^{2} = x (x \pm p) (x \pm q) $ over imaginary quadratic number fields of class number one fra arXiv Front: math.NT av Xiumei Li Let $ p $ and $ q $ be odd prime numbers with $ q - p = 2, $ the $\varphi -$Selmer groups, Shafarevich-Tate groups ($ \varphi - $ and $ 2-$part) and their dual ones as well the Mordell-Weil groups of elliptic curves $ y^{2} = x (x \pm p) (x \pm q) $ over imaginary quadratic number fields of class number one are determined explicitly in many cases.
<]]>- Elliptic genusWrite comment View comments
Ask Carl McTague!
Elliptic genera, real algebraic varieties etc
Ando and Greenlees on rational equivariant sigma-genus
<]]>- Enriched category theoryWrite comment View comments
See Kelly.
Borceaux vol 2 chapter 6
<]]>- Enumerative algebraic geometryWrite comment View comments
I think this is mentioned by Andre as one of the motivations for the theory of motives. There is also, I believe, a Park/IAS book covering something related to this.
Title: 13/2 ways of counting curves Authors: R. Pandharipande, R. P. Thomas Categories: math.AG Algebraic Geometry (math.SG Symplectic Geometry; physics.hep-th High Energy Physics - Theory) Comments: Small corrections. 50 pages, 4 figures. To appear in proceedings of "School on Moduli Spaces", Isaac Newton Institute, Cambridge 2011 MSC: 14N35, 14N Abstract: In the past 20 years, compactifications of the families of curves in algebraic varieties X have been studied via stable maps, Hilbert schemes, stable pairs, unramified maps, and stable quotients. Each path leads to a different enumeration of curves. A common thread is the use of a 2-term deformation/obstruction theory to define a virtual fundamental class. The richest geometry occurs when X is a nonsingular projective variety of dimension 3. We survey here the 13/2 principal ways to count curves with special attention to the 3-fold case. The different theories are linked by a web of conjectural relationships which we highlight. Our goal is to provide a guide for graduate students looking for an elementary route into the subject.
<]]>- Equivariant homotopy theoryWrite comment View comments
There is a old book by May, Lewis, Steinberger. I think there is also a new book by May et al.
Preprints/articles by May and Guillou, see arxiv or their webpages.
Mandell and May: Equivariant orthogonal spectra and S-modules.
Adams: Prerequisites (on equivariant stable homotopy theory) for Carlsson's lectures. In LNM1051 (1982)
Blumberg: Continuous functors as a model for the equivariant stable homotopy category. http://arxiv.org/abs/math/0505512
http://golem.ph.utexas.edu/category/2010/01/equivariant_stable_homotopy_th.html
<]]>- EsnaultWrite comment View comments
- <]]>
- Etale homotopy theoryWrite comment View comments
Something by Ambrus Pal?
Pal conversation (Sep 2011). There is an absolute and a relative homotopy type. The relative one comes with a Galois action. These things are objects in Pro-Ho(sSet) and Pro-Ho(G-sSet) respectively. For the homotopy theory of the latter, see a paper of Goerss (profinite gps...). There is an A1-invariance theorem in Friedlander somewhere, at least for the absolute. One can also work with Pro-objects in the model cat and not the homotopy cat, but then one has to work with rigidified hypercoverings, i.e. geometrically pointed hypercoverings.
Pal said a hypercovering is a simplicial object in the cat of coverings, which is Kan contractible, i.e. trivially fibrant.
arXiv:1110.0164 Homotopy Obstructions to Rational Points from arXiv Front: math.AT by Yonatan Harpaz, Tomer M. Schlank In this paper we propose to use a relative variant of the notion of the étale homotopy type of an algebraic variety in order to study the existence of rational points on it. In particular, we use an appropriate notion of homotopy fixed points in order to construct obstructions to the local-global principle. The main results in this paper are the connections between these obstructions and the classical obstructions, such as the Brauer-Manin, the étale-Brauer and certain descent obstructions. These connections allow one to understand the various classical obstructions in a unified framework.
Artin and Mazur LNM0100. Ass to any locally noetherian prescheme a pro-object in the homotopy cat of simplicial sets, called the etale homotopy type. For a complex variety, this is a certain profinite completion of the usual homotopy type. We develop homotopy theory for pro-simplicial sets, Hurewicz, Whitehead, Postnikoff etc. Relation to questions about independence of embedding. Finiteness of the number of (stable) homotopy types with isomorphic profinite completion. Galois action on the l-adic homotopy type of a variety - this contains more info than cohomology if the var is not abelian. Actual def of etale homotopy type: Take C a locally connected site. Let HR(C) be the cat of hypercoverings of C. Apply the functor pi to the category gives a pro-object in the homotopy cat of simplicial sets. This gives the Verdier functor from locally conn sites to such pro-objects. Here the functor pi is the "connected components functor" from C to Sets. So the "index cat" for the pro-simplicial set is a cat of hypercoverings. Take C to be the etale site over X. Get pro-homotopy and pro-homology groups of C, and also cohomology etc.
Toen: Segal topoi and stacks over Segal categories. File Toen web prepr msri.pdf. Analogous and in some sense equivalent to the notion of model topos, but some advantages. Includes a Giraud type statement characterizing Segal topoi among Segal cats. Notion of homotopy type of a Segal site, improving on the etale homotopy theory of schemes, and more generally on the theory of homotopy types of sites as defined by Artin and Mazur.
arXiv:1002.1423 The Étale Homotopy Type and Obstructions to the Local-Global Principle from arXiv Front: math.AT by Yonatan Harpaz, Tomer M. Schlank In 1969 Artin and Mazur defined the étale homotopy type of an algebraic variety \cite{AMa69}. In this paper we define various obstructions to the local-global principle on a variety $X$ over a global field using the étale homotopy type of $X$ and the concept of homotopy fixed points. We investigate relations between those "homotopy obstructions" and connect them to various known obstructions such as the Brauer -Manin obstruction, the étale-Brauer obstruction and finite descent obstructions. This gives a reinterpretation of known arithmetic obstructions in terms of homotopy theory.
arXiv:1109.5477 A Projective Model Structure on Pro Simplicial Sheaves, and the Relative Étale Homotopy Type from arXiv Front: math.AG by Ilan Barnea, Tomer M. Schlank In \cite{Isa}, Isaksen showed that a proper model category $\cC$, induces a model structure on the pro category $Pro(\cC)$. In this paper we generalize Isaksen's theorem to the case when $\cC$ possess a weaker structure, which we call a "weak fibration category". Namely, we show that if $\cC$ is a weak fibration category, that satisfies an extra condition, there is a naturally induced model structure on $Pro(\cC)$. We then apply our theorem to the case when $\cC$ is the weak fibration category of simplicial sheafs on a Grothendieck site, where both weak equivalences and fibrations are local as in \cite{Jar}. This gives a new model structure on the category of pro simplicial sheaves. Using this new model structure we give a definition of the étale homotopy type of Artin and Mazur \cite{AM}, as the result of applying a derived functor. Our definition actually gives as object in $Pro(\cS)$ and not just in $Pro(Ho(\cS))$ as in \cite{AM}. Our definition also extends naturally to a relative notion of the étale homotopy type, as considered for example in \cite{HaSc}.
arXiv:1002.3532 Etale Homotopy Types and Bisimplicial Hypercovers from arXiv Front: math.AT by Michael D. Misamore An étale homotopy type $T(X, z)$ associated to any pointed locally fibrant connected simplicial sheaf $(X, z)$ on a pointed locally connected small Grothendieck site $(\model category{C}, x)$ is studied. It is shown that this type $T(X, z)$ specializes to the étale homotopy type of Artin-Mazur for pointed connected schemes $X$, that it is invariant up to pro-isomorphism under pointed local weak equivalences (but see \cite{Schmidt1} for an earlier proof), and that it recovers abelian and nonabelian sheaf cohomology of $X$ with constant coefficients. This type $T(X, z)$ is compared to the étale homotopy type $Tb(X, z)$ constructed by means of diagonals of pointed bisimplicial hypercovers of $x = (X, z)$ in terms of the associated categories of cocycles, and it is shown that there are bijections \pi0 H{\hyp}(x, y) \cong \pi0 H{\bihyp}(x, y) at the level of path components for any locally fibrant target object $y$. This quickly leads to natural pro-isomorphisms $T(X, z) \cong Tb(X, z)$ in $\Ho{\sSet\ast}$. By consequence one immediately establishes the fact that $Tb(X, z)$ is invariant up to pro-isomorphism under pointed local weak equivalences. Analogous statements for the unpointed versions of these types also follow.
arXiv:1002.3530 Nonabelian $H^1$ and the Étale van Kampen Theorem from arXiv Front: math.AG by Michael D. Misamore Generalized étale homotopy pro-groups $\pi1^{\ets}(\model category{C}, x)$ associated to pointed connected small Grothendieck sites $(\model category{C}, x)$ are defined and their relationship to Galois theory and the theory of pointed torsors for discrete groups is explained. Applications include new rigorous proofs of some folklore results around $\pi1^{\ets}(\et{X}, x)$, a description of Grothendieck's short exact sequence for Galois descent in terms of pointed torsor trivializations, and a new étale van Kampen theorem which gives a simple statement about a pushout square of pro-groups that works for covering families which do not necessarily consist exclusively of monomorphisms. A corresponding van Kampen result for Grothendieck's profinite groups $\pi_1^{\Gals}$ immediately follows.
<]]>- ETNCWrite comment View comments
Snaith in Axiomatic, enriched, and motivic homotopy theory gives an overview of some aspects.
See various papers by Chinburg, Kolster, Pappas, Snaith, Burns, Greither, Flach, Breuning.
Something really nice was written by Chris Wuthrich I believe.
arXiv:1210.8298 On the equivariant Tamagawa number conjecture for Tate motives and unconditional annihilation results fra arXiv Front: math.NT av Henri Johnston, Andreas Nickel Let L/K be a finite Galois extension of number fields with Galois group G. Let p be a rational prime and let r be a non-positive integer. By examining the structure of the p-adic group ring Z_p[G], we prove many new cases of the p-part of the equivariant Tamagawa number conjecture (ETNC) for the pair (h^0(Spec(L)(r),Z[G])). The same methods can also be applied to other conjectures concerning the vanishing of certain elements in relative algebraic K-groups. We then prove a recent conjecture of Burns concerning the annihilation of class groups as Galois modules for a wide class of interesting extensions, including cases in which the full ETNC in not known. In the same vein, we construct annihilators of higher dimensional algebraic K-groups of the ring of integers in L.
Citat: ETNC
One of the most fascinating topics in Algebraic Number Theory and - more generally - in Arithmetic Algebraic Geometry is the arithmetic interpretation of special values at integer points of L-functions attached to varieties over a number field . Classical examples are provided by the analytic class number formula of Dirichlet, which describes the residue at 1 of the zeta-function of a number field in terms of the Dirichlet regulator, the class number and the order of the group of roots of unity, and by the Conjecture of Birch and Swinnerton-Dyer, which predicts the order of vanishing of the L-function of an elliptic curve E over the rationals at 1, and expresses the leading term via arithmetic data attached to E. A far-reaching generalization to L-functions of arbitrary smooth projective varieties (or motives ) over a number field is due to Bloch-Kato. They conjecturally described the leading terms of the values of the L-functions at integer points in terms of Tamagawa numbers. Using a reformulation of the Bloch-Kato Conjecture due to Fontaine and Perrin-Riou - and independently Kato -, Burns and Flach extended the conjecture to take into account the action of endomorphisms of the variety. This Equivariant Tamagawa Number Conjecture (ETNC) encompasses the refinements of various classical conjectures, e.g. Gross' refinement of the Birch and Swinnerton-Dyer Conjecture for CM elliptic curves, and all the conjectures of Chinburg and others in Galois module theory.
In the special case of the Dedekind zeta-function of a number field the original Bloch-Kato Conjecture is equivalent to a cohomological version of a conjecture of Lichtenbaum, which expresses the leading term of the zeta-function at negative integers as a non-zero rational multiple of the Borel regulator, where the rational number is given as an Euler characteristic in etale cohomology. For abelian number fields this conjecture was proved in 1996 by Nguyen Quang Do, Kolster and Fleckinger up to powers of 2. In the last 3 years there has been increased activity in this field with striking results: Benois and Nguyen Quang Do proved the full Bloch-Kato Conjecture for abelian number fields (up to powers of 2) by showing the compatability of the conjecture with the functional equation, Ritter and Weiss proved an equivariant version of the so-called Main Conjecture in Iwasawa-theory - a key ingredient in the study of the ETNC - for relative abelian extensions, which implied the validity of the ETNC for values at 0 for abelian fields, Huber and Kings gave a different approach to parts of these results using Euler systems, and finally Burns and Greither proved the ETNC for all abelian number fields - as always up to powers of 2.
<]]>- Euler characteristicWrite comment View comments
Fiore et al on Euler char of categories.
arXiv:1007.3868 Euler Characteristics of Categories and Homotopy Colimits from arXiv Front: math.CT by Thomas M. Fiore, Wolfgang Lück, Roman Sauer In a previous article, we introduced notions of finiteness obstruction, Euler characteristic, and L^2-Euler characteristic for wide classes of categories. In this sequel, we prove the compatibility of those notions with homotopy colimits of I-indexed categories where I is any small category admitting a finite I-CW-model for its I-classifying space. Special cases of our Homotopy Colimit Formula include formulas for products, homotopy pushouts, homotopy orbits, and transport groupoids. We also apply our formulas to Haefliger complexes of groups, which extend Bass--Serre graphs of groups to higher dimensions. In particular, we obtain necessary conditions for developability of a finite complex of groups from an action of a finite group on a finite category without loops.
http://mathoverflow.net/questions/35156/how-do-you-define-the-euler-characteristic-of-a-scheme
<]]>- Euler systemWrite comment View comments
See the book of Coates and Sujatha.
MR1749177 (2001g:11170) Rubin, Karl Euler systems.
Scholl: Article in the LMS volume on Galois reps, I think
http://mathoverflow.net/questions/11421/is-higher-k-functor-the-derived-functor-of-k0
[arXiv:0706.0377] $\Lambda$-adic Kolyvagin systems from arXiv Front: math.NT by Kazim Buyukboduk In this paper, we study the deformations of Kolyvagin systems that are known to exist in a wide variety of cases, by the work of B. Howard, B. Mazur, and K. Rubin for the residual Galois representations, along the cyclotomic Iwasawa algebra. We prove, under certain technical hypotheses, that a cyclotomic deformation of a Kolyvagin system exists. We also briefly discuss how our techniques could be extended to prove that one could deform Kolyvagin systems for other deformations as well.
We discuss several applications of this result, particularly relation of these $\Lambda$-adic Kolyvagin systems to p-adic L-functions (in view of the conjectures of Perrin-Riou on p-adic L-functions) and applications to main conjectures; also applications to the study of Iwasawa theory of Rubin-Stark units.arXiv:1103.5982 On Euler systems of rank $r$ and their Kolyvagin systems from arXiv Front: math.NT by Kazim Buyukboduk In this paper we set up a general Kolyvagin system machinery for Euler systems of rank r (in the sense of Perrin-Riou) associated to a large class of Galois representations, building on our previous work on Kolyvagin systems of Rubin-Stark units and generalizing the results of Kato, Rubin and Perrin-Riou. Our machinery produces a bound on the size of the classical Selmer group attached to a Galoys representation T (that satisfies certain technical hypotheses) in terms of a certain r \times r determinant; a bound which remarkably goes hand in hand with Bloch-Kato conjectures. At the end, we present an application based on a conjecture of Perrin-Riou on p-adic L-functions, which lends further evidence to Bloch-Kato conjectures.
<]]>- Ex-infty functorWrite comment View comments
Kan's
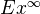 functor, see Goerss-Jardine section III.4. It maps a simplicial set into a Kan complex via a WE. The construction is preserved by left exact functors which have right adjoints.<]]>
functor, see Goerss-Jardine section III.4. It maps a simplicial set into a Kan complex via a WE. The construction is preserved by left exact functors which have right adjoints.<]]>- Exact categoryWrite comment View comments
This can mean several different things. See nLab for one of them. Exact category: Means one thing in Borceaux vol 2 and another thing inn Quillen.
http://ncatlab.org/nlab/show/Quillen+exact+category
For an expose of the Quillen stuff, see Buehler
In the 50s, this was defined by Buchsbaum as "an abelian category but without the requirement that direct sums exist". Is this also the modern definition?
LNM0236 treats exact and regular categories, and "categories of sheaves", but doesn't look terribly interesting at first sight
<]]>- Exact functorWrite comment View comments
- <]]>
- Exponential sumsWrite comment View comments
- <]]>