Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- FaltingsWrite comment View comments
- <]]>
- Farrell-Jones conjectureWrite comment View comments
Possibly the same as the Isomorphism conjecture? See K0514. A survey.
On the conjectures of Novikov, Borel, Farrell-Jones, and Baum-Connes: See Kreck and Lueck book in the K-theory folder.
See K-theory handbook chapter
<]]>- FeliuWrite comment View comments
- <]]>
- Fesenko programWrite comment View comments
Ivan Fesenko (Nottingham) "Understanding the conjecture of Birch and Swinnerton-Dyer"
Abstract: To every elliptic curve over a global field one can associate a regular proper model which is geometrically a two-dimensional object and which reveals more underlying structures and dualities than its generic fibre. Unlike the classical adelic structure on one-dimensional arithmetic schemes, there are two adelic structures on arithmetic surfaces: one is more suitable for geometry and another is more suitable for analysis and arithmetic. The two-dimensional adelic analysis studies the zeta function of the surface lifting it to a zeta integral using the second adelic structure. Its main theorem reduces the study of analytic properties of the zeta integral to those of a boundary term which is an integral over the weak boundary of adelic spaces of the second type. To study the latter one uses the symbol map from K1 of the first adelic structure and K1 of the second adelic structure to K_2 of the first adelic structure. The (known in some partial cases but not really understood) equality of the analytic and arithmetic ranks becomes much more transparent and natural in the language of the two adelic structures on the surface and their interplay. Moreover, the adelic approach includes a potential to explain the finiteness of the Brauer-Grothendieck group of the surface and hence of Shah.
<]]>- Feynman diagramsWrite comment View comments
For Feynman diagrams and the relation to mixed Tate motives, see Bloch, Esnault, Kreimer: Om motives associated to graph polynomials, and its long review. Also, Bloch: Motives ass to graphs.
<]]>- FiberWrite comment View comments
In a pointed category with colimits and limits, we define the fiber, or kernel, of a map
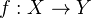 to be the equalizer
to be the equalizer 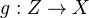 of
of  and the zero map.<]]>
and the zero map.<]]>- Fiber sequenceWrite comment View comments
Let
 be a Pointed model category. A fiber sequence in
be a Pointed model category. A fiber sequence in  is a diagram
is a diagram 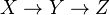 in
in 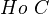 together with a right action of
together with a right action of 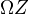 on
on  that is IMic in
that is IMic in 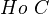 to a diagram of the form
to a diagram of the form 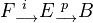 where
where 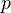 is a fibration of fibrant objects in
is a fibration of fibrant objects in  with fiber
with fiber 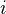 and where
and where  has the standard right action by
has the standard right action by 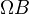 .
.To a fiber sequence one can associate a boundary map
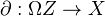 . See Hovey p. 156.
. See Hovey p. 156.Fiber sequences have properties dual to those of a Cofiber sequence
<]]>- Fiber spaceWrite comment View comments
Cartan: Bourbaki Exp 34: Espaces fibres analytiques complexes
Koszul: Bourbaki exp 38: Cohomologie des espaces fibres differentiables et connexions
Serre exp 54: Steenrod ops and fiber spaces
Serre exp 82: Espaces fibres algebriques
<]]>- Fibered categoryWrite comment View comments
nLab uses the term Grothendieck fibration
http://ncatlab.org/nlab/show/n-fibration
Fibred category: Borceaux vol 2 chapter 8
<]]>- Fibrant objectWrite comment View comments
In a model category, an object is called fibrant if the map from it to the terminal object is a fibration.
<]]>- Fibrant replacementWrite comment View comments
Similar to the Cofibrant replacement, for any object
 there is a fibrant object
there is a fibrant object 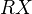 with a trivial cofibration
with a trivial cofibration 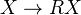 .<]]>
.<]]>- FibrationWrite comment View comments
Fibrations are part of a model structure.
http://ncatlab.org/nlab/show/fibration+of+simplicial+sets
Fibrations (trivial cofibrations) are closed under pullbacks.
A variety of different notions of fibration can be found in HTT
http://www.ncatlab.org/nlab/show/fibrations+of+quasi-categories
nLab on Grothendieck fibration
http://ncatlab.org/nlab/show/fibration+sequence
http://mathoverflow.net/questions/49759/definition-of-fibration-in-algebraic-geometry
<]]>- Fibre bundleWrite comment View comments
LNM0036 Topics in the homology of fibre bundles, by Borel. Gives and old-fashioned, and hence maybe better in some sense, of fibre bundles, H-spaces, and more.
Fibre bundles folder including Husemoller book
<]]>- FieldWrite comment View comments
Fried and Jarden: Field arithmetic
<]]>- Field with one elementWrite comment View comments
Many people have expressed hopes for a definition of the "field with one element", which would be useful in various aspects of arithmetic geometry. Some approaches: Soulé and Durov
See stuff on the web page of Consani, and her talk from the Toronto workshop.
Blogs! See neverendingbooks and F_un mathematics
Field with one element folder, under N TH
arXiv:1103.1745 The geometry of blueprints. Part I: Algebraic background and scheme theory from arXiv Front: math.AG by Oliver Lorscheid A blueprint generalizes both commutative (semi-)rings and commutative monoids. This generalization allows a simultaneous treatment of ideals resp. congruences for rings and monoids and leads to a common scheme theory. In particular, it bridges the gap between usual schemes and $\mathbb{F}1$-schemes (after Kato, Deitmar and Connes-Consani). Beside this unification, the category of blueprints contains new interesting objects as "improved" cyclotomic field extensions $\mathbb{F}{1^n}$ of $\mathbb{F}1$ and "archimedean valuation rings". It also yields a notion of semi-ring schemes.This first paper lays the foundation for subsequent projects, which are devoted to the following problems: Tits' idea of Chevalley groups over $\mathbb{F}1$, congruence schemes, sheaf cohomology and $K$-theory and a unified view on analytic geometry over $\mathbb{F}_1$, adic spaces (after Huber), analytic spaces (after Berkovich) and tropical geometry.
F1 library folder under N TH
arXiv:1103.1235 Reconstructing the spectrum of F1 from the stable homotopy category from arXiv Front: math.AT by Stella Anevski The finite stable homotopy category S0 has been suggested as a candidate for a category of perfect complexes over the monoid scheme Spec F1. We apply a reconstruction theorem from algebraic geometry to S0, and show that one recovers the one point topological space. We also classify filtering subsets of the set of principal thick subcategories of S_0, and of its p-local versions. This is motivated by a result saying that the analogous classification for the category of perfect complexes over an affine scheme provides topological information.
arXiv:1009.0121 Construction of schemes over $F1$, and over idempotent semirings: towards tropical geometry from arXiv Front: math.AG by Satoshi Takagi In this paper, we give some categorical description of the general spectrum functor, defining it as an adjoint of a global section functor. The general spectrum functor includes that of $F1$ and of semirings.
Toen and Vaquie: Under Spec Z. Some notes: Idea: Think of commutative monoids in a symm monoidal cat C as models for affine schemes relative to C. If there is a reasonable symmetric monoidal functor from C to Z-modules, get a base change functor, and a notion of scheme under Spec(Z). Homotopical version of this requires C to have a model structure. Now have flat and Zariski topology. Can make sense of schemes: a functor with a Zariski covering. Stuff about toric varieties and GL. Brave new AG over the sphere spectrum, and the spectrum with one element.
arXiv:1102.4046 Congruence schemes from arXiv Front: math.AG by Anton Deitmar A new category of algebro-geometric objects is defined. This construction is a vast generalization of existing F1-theories, as it contains the the theory of monoid schemes on the one hand and classical algebraic theory, e.g. Grothendieck schemes, on the the other. It also gives a handy description of Berkovich subdomains and thus contains Berkovich's approach to abstract skeletons. Further it complements the theory of monoid schemes in view of number theoretic applications as congruence schemes encode number theoretical information as opposed to combinatorial data which are seen by monoid schemes.
[arXiv:0907.3824] Algebraic groups over the field with one element from arXiv Front: math.AG by Oliver Lorscheid Remarks in a paper by Jacques Tits from 1956 led to a philosophy how a theory of split reductive groups over $\F1$, the so-called field with one element, should look like. Namely, every split reductive group over $\Z$ should descend to $\F1$, and its group of $\F1$-rational points should be its Weyl group. We connect the notion of a torified variety to the notion of $\F1$-schemes as introduced by Connes and Consani. This yields models of toric varieties, Schubert varieties and split reductive groups as $\Fun$-schemes. We endow the class of $\F1$-schemes with two classes of morphisms, one leading to a satisfying notion of $\F1$-rational points, the other leading to the notion of an algebraic group over $\F1$ such that every split reductive group is defined as an algebraic group over $\F1$. Furthermore, we show that certain combinatorics that are expected from parabolic subgroups of $\GL(n)$ and Grassmann varieties are realized in this theory.
arXiv:0908.3124 A theory of base motives from arXiv Front: math.AG by Jack Morava A category of correspondences based on Waldhausen A-theory has interesting analogies, in the context of differential topology, to categories of mixed Tate motives studied in arithmetic geometry.
In particular, the Hopf object S \wedge_A S (regarding A(*) as a kind of local ring over the sphere spectrum) has some similarities to a motivic group for this category; its associated rational Lie algebra is free, on odd-degree generators...[arXiv:0909.0069] Mapping F1-land:An overview of geometries over the field with one element from arXiv Front: math.AG by Javier López Peña, Oliver Lorscheid This paper gives an overview of the various approaches towards F1-geometry. In a first part, we review all known theories in literature so far, which are: Deitmar's F1-schemes, Toën and Vaquié's F1-schemes, Haran's F-schemes, Durov's generalized schemes, Soulé's varieties over F1 as well as his and Connes-Consani's variations of this theory, Connes and Consani's F1-schemes, the author's torified varieties and Borger's Lambda-schemes. In a second part, we will tie up these different theories by describing functors between the different F1-geometries, which partly rely on the work of others, partly describe work in progress and partly gain new insights in the field. This leads to a commutative diagram of F1-geometries and functors between them that connects all the reviewed theories. We conclude the paper by reviewing the second author's constructions that lead to realization of Tits' idea about Chevalley groups over F_1.
arXiv:1009.3235 On the Algebraic K-theory of Monoids from arXiv Front: math.KT by Chenghao Chu, Jack Morava Let $A$ be a not necessarily commutative monoid with zero such that projective $A$-acts are free. This paper shows that the algebraic K-groups of $A$ can be defined using the +-construction and the Q-construction. It is shown that these two constructions give the same K-groups. As an immediate application, the homotopy invariance of algebraic K-theory of certain affine $\mathbb{F}1$-schemes is obtained. From the computation of $K2(A),$ where $A$ is the monoid associated to a finitely generated abelian group, the universal central extension of certain groups are constructed.
<]]>- Field with one element IIWrite comment View comments
http://mathoverflow.net/questions/2300/what-is-the-field-with-one-element
http://mathoverflow.net/questions/1628/kf-1-sphere-spectrum
http://ncatlab.org/nlab/show/field+with+one+element
http://www.noncommutative.org/index.php/the-smirnov-letters.html
http://www.noncommutative.org/index.php/prep-notes-dump.html
http://www.noncommutative.org/index.php/mathbbf_1-and-noncommutative-geometry.html
http://matrix.cmi.ua.ac.be/fun/index.php/connesconsani2011.html
See all arxiv articles of Connes, Consani, maybe Marcolli
arXiv:0911.3537 Characteristic one, entropy and the absolute point from arXiv Front: math.NT by Alain Connes, Caterina Consani We show that the mathematical meaning of working in characteristic one is directly connected to the fields of idempotent analysis and tropical algebraic geometry and we relate this idea to the notion of the absolute point. After introducing the notion of "perfect" semi-ring of characteristic one, we explain how to adapt the construction of the Witt ring in positive characteristic to the limit case of characteristic one. This construction unveils an interesting connection with entropy and thermodynamics, while shedding a new light on the classical Witt construction itself. We simplify our earlier construction of the geometric realization of an F1-scheme and extend our earlier computations of the zeta function to cover the case of F1-schemes with torsion. Then, we show that the study of the additive structures on monoids provides a natural map from monoids to sets which comes close to fulfill the requirements for the hypothetical curve compactifying Spec Z over the absolute point. Finally, we test the computation of the zeta function on elliptic curves over the rational numbers.
arXiv:0910.3879 Meromorphicity of some deformed multivariable zeta functions for $F1$-schemes from arXiv Front: math.NT by Norihiko Minami Motivated by recent work of Deitmar-Koyama-Kurokawa, Kurokawa-Ochiai, Connes-Consani, and the author, we define some multivariable deformed zeta functions of Hurwitz-Igusa type for a Noetherian $\F1$-scheme $X$ in the sense of Connes-Consani.
Our zeta functions generalize both the zeta functions studied by Deitmar-Koyama-Kurokawa, Kurokawa-Ochiai, and the log derivative of the modified Soulé type zeta function Connes-Consani.We give an explicit presentation for these zeta functions using the Hurwitz zeta functions, and so, we can derive its meromorphicity.When restricted to the log derivative of the modified Soulé type zeta functions, we find our invariant $\mu(A)$ for a finite abelian group $A$, introduced in ArXiv-0907.0918v2, plays an extremely important role in the Soulé type zeta functions.<]]>- Field with one element IIIWrite comment View comments
Title: G-Theory of \F1-Algebras I: the Equivariant Nishida Problem http://front.math.ucdavis.edu/1110.6001 Authors: Snigdhayan Mahanta Categories: math.AT Algebraic Topology (math.KT K-Theory and Homology; math.RA Rings and Algebras) Comments: 24 pages; v2 introduction rewritten, references added Abstract: We develop a version of G-theory for \F1-algebras and establish its first properties. We construct a Cartan assembly map to compare the Chu-Morava K-theory for finite pointed groups with our G-theory. We compute the G-theory groups for finite pointed groups in terms of stable homotopy of some classifying spaces. We also construct combinatorial Grayson operations on them. We discuss how our formalism is relevant to the Equivariant Nishida Problem - it asks whether there are operations on \S^G that endow \oplusn\pi{2n}(\S^G) with a pre-\lambda-ring structure, where G is a finite group and \S^G is the G-fixed point spectrum of the equivariant sphere spectrum.
I have some scrap notes, probably from a talk by Vezzani, where he compares a so called ``geometric'' approach with the TV approach. Here Rings corresponds to Ab, Monoids with partially defined addition corr to the slice category of pointed sets over Ab (Kahn: But these are affine log schemes!), Monoids corr to Set, and Monoids with zero corr to pointed sets.
For blueprint geometry, see several papers by Lorscheid and/or Lopez Pena. Here is a blog post mentioning connections with Reineke's observation, and explains that a blue scheme can be an elliptic curve: http://www.neverendingbooks.org/index.php/quiver-grassmannians-and-mathbbf_1-geometry.html
Takagi has an arxiv preprint on convexoid rings, claiming to construct a compactification of Spec Z.
<]]>- Finitely generated model categoryWrite comment View comments
See Hovey p. 190.
<]]>- Finiteness conditions for simplicial sheavesWrite comment View comments
Could someone give an overview, or just some examples, of "finiteness conditions" for simplicial sheaves/presheaves and/or simplicial schemes? Any answer or comment about this would be interesting, but I am interested in particular in the following two things:
1) I once heard Toen say something about this, and that one can express some kind of condition on simplicial sheaves/presheaves/schemes in terms of convergence of some power series, or something along these lines. What kind of power series is this, and what are the definitions/statements?
2) As explained for example in Deligne's classical papers on Hodge theory, a cohomology theory for varieties (defined as hypercohomology of a complex of sheaves, say) can be extended to simplicial varieties using a spectral sequence. I suspect (but am not sure) that this works well in some sense only under some kind of condition on the simplicial variety, but what would such a condition be?
Some background: I am interested primarily in simplicial sheaves/presheaves on a site coming from algebraic geometry, which would typically be some category of schemes equipped with the Zariski/Nisnevich/etale/flat topology. A simplicial sheaf/presheaf should be thought of a "generalized space", some of the most important examples being the "motivic spaces" in A1-homotopy theory, and stacks in the sense of Toen.
Cisinski on Math Overflow:
I don't know what Toën was talking about, but I suspect that it was about finiteness conditions for Artin stacks: the problem is that the usual finiteness conditions we look at for schemes (like the notion of constructibility for l-adic sheaves) do not extend to stacks in a straightforward way, which gives some trouble if one wants to count points (i.e. to define things like Euler characteristics). Some notions of finiteness are developed to define Grothendieck rings of Artin stacks (e.g. in Toën's paper arXiv:0509098 and in Ekedahl's paper arXiv:0903.3143), which can be realized by our favourite cohomologies (l-adic, Hodge, etc), but the link with a good notion of finiteness for categories of coefficients over Artin stacks (l-adic sheaves, variation of mixed Hodge structures) does not seem to be fully understood yet, at least conceptually (and by myself).
As for finiteness conditions for sheaves (in some homotopical context), the kind of properties we might want to look at are of the following shape.
Consider a variety of you favourite kind X, and a derived category D(X) of sheaves over some site S associated to X (e.g. open, or étale, or smooth subvarieties over X etc.). For instance, D(X) might be the homotopy category of the model category of simplicial sheaves, or the derived category of sheaves of R-modules. Important finiteness properties can be expressed by saying that for any U in the site S, we have
(1) hocolimᵢ RΓ(U,Fᵢ)= RΓ(U,hocolimᵢ Fᵢ)
where {Fᵢ} is a filtered diagram of coefficients. If you are in such a context, then you can look at the compact objects in D(X), i.e. the objects A of D(X) such that
(2) hocolimᵢ RHom(A,Fᵢ)= RHom(A,hocolimᵢ Fᵢ)
for any filtered diagram {Fᵢ}. In good situations, condition (1) will imply that the category of compact objects will coincide with constructible objects (i.e. the smallest subcategory of D(X) stable under finite homotopy colimits (finite meaning: indexed by finite posets) which contains the representable objects).
Sufficient conditions to get (1) are the following:
a) For simplicial sheaves (as well as sheaves of spectra or R-modules...), a sufficient condition is that the topology on S is defined by a cd-structure in the sense of Voevodsky (see arXiv:0805.4578). These include the Zariski topology, the Nisnevich topology, as well as the cdh topology (the latter being generated by Nisnevich coverings as well as by blow-ups in a suitable sense), at least if we work with noetherian schemes of finite dimension. Note also that topologies associated to cd structures define what Morel and Voevodsky call a site of finite type (in the language of Lurie, this means that, for such sites, the notion of descent is the same as the notion of hyperdescent: descent for infinity-stacks over S can be tested only using truncated hypercoverings; this is the issue discussed by David Ben Zvi above). In practice, the existence of a cd structure allows you to express (hyper)descent using only Mayer-Vietoris-like long exact sequences (the case of Zariski topology was discovered in the 70's by Brown and Gersten, and they used it to prove Zariski descent for algebraic K-theory).
b) For complexes of sheaves of R-modules, a sufficient set of conditions are
i) the site S is coherent (in the sense of SGA4).
ii) any object of the site S is of finite cohomological dimension (with coefficients in R).
The idea to prove (1) under assumption b) is that one proves it first when all the Fᵢ's are concentrated in degree 0 (this is done in SGA4 under assumption b)i)). This implies the result when the Fᵢ's are uniformly bounded. Then, one uses the fact, that, under condition b)ii), the Leray spectral sequence converges strongly, even for unbounded complexes (this done at the begining of the paper of Suslin and Voevodsky "Bloch-Kato conjecture and motivic cohomology with finite coefficients").
This works for instance for étale sheaves of R-modules, where R=Z/n, with n prime to the residual characteristics. Note moreover that, in the derived category of R-modules, the compact objects (i.e. the complexes A satisfying (2)) are precisely the perfect complexes. The fact that the six Grothendieck operations preserves constructibility can then be translated into the finiteness of cohomology groups (note however that the notion of constructiblity is more complex then this in general: if we work with l-adic sheaves (with Ekedahl's construction, for instance), then the notion of constructiblity does not agree with compactness anymore). However, condition (1) is preserved after taking the Verdier quotient of D(X) by any thick subcategory T obtained as the smallest thick subcategory which is closed under small sums and which contains a given small set of compact objects of D(X) (this is Thomason's theorem). This is how such nice properties survive in the context of homotopy theory of schemes for instance. Note also that, in a stable (triangulated) context, condition (2) for A implies that we have the same property, but without requiring the diagrams {Fᵢ} to be filtering.
For your second question, the extension of a cohomology theory to simplicial varieties is automatic (whenever the cohomology is given by a complex of presheaves), at least if we have enough room to take homotopy limits, which is usually the case (and not difficult to force if necessary). The only trouble is that you might lose the finiteness conditions, unless you prove that your favorite simplicial object A satisfies (2). The fact that Hironaka's resolution of singularities gives the good construction (i.e. gives nice objects for open and/or singular varieties) can be expained by finiteness properties related to descent by blow-ups (i.e. cdh descent), but the arguments needed for this use strongly that we work in a stable context (I don't know any argument like this for simplicial sheaves). The fuzzy idea is that if a cohomology theory satisfies Nisnevich descent and homotopy invariance, then it satisfies cdh descent (there is a nice very general proof of this in Voevodsky's paper arXiv:0805.4576 (thm 4.2, where you will see we need to be able to desuspend)); then, thanks to Hironaka, locally for the cdh topology, any scheme is the complement of a strict normal crossing divisor in a projective and smooth variety. As cdh topology has nice finiteness properties (namely a)), and as any k-scheme of finite type is coherent in the cdh topos, this explains, roughly, why we get nice extensions of our cohomology theories (as far as you had a good knowledge of smooth and projective varieties). If we work with rational coefficients, the same principle applies for schemes over an excellent noetherian scheme S of dimension lesser or equal to 2, using de Jong's results instead of Hironaka's, and replacing the cdh topology by the h topology (the latter being obtained from the cdh topology by adding finite surjective morphisms): it is then sufficient to have a good control of proper regular S-schemes.
<]]>- Finiteness propertiesWrite comment View comments
Material on Serre classes?
de Jong explains perfect and compact objects: http://math.columbia.edu/~dejong/wordpress/?p=2253
<]]>- Finiteness theoremsWrite comment View comments
Question: Can we use homotopy theory to prove finiteness results in arithmetic geometry? (Morel)
Déglise and Cisinski has a finiteness theorem on p 8 of Triangulated preprint, related to mixed Weil cohomologies.
Bondal and Van den Bergh: Generators etc. Some results on finiteness of global Exts, I think. This paper is mentioned in Toen: Champs affines.
arXiv:1103.5544 Finite generation conjectures for cohomology over finite fields from arXiv Front: math.KT by Thomas H Geisser We construct an intermediate cohmology between motivic cohomology and Weil-etale cohomology. Using this, the Bass conjecture on finite generation of motivic cohomology, and the Beilinson-Tate on the finite generation of Weil-etale cohomology are related.
Dan Petersen MO answer on realizing homotopy types by finite topological spaces
arXiv:1205.6148 DG categories and exceptional collections from arXiv Front: math.AG by Agnieszka Bodzenta Bondal and Kapranov describe how to assign to a full exceptional collection on a variety X a DG category C such that the bounded derived category of coherent sheaves on X is equivalent to the bounded derived category of C. In this paper we show that the category C has finite dimensional spaces of morphisms. We describe how it behaves under mutations and present an algorithm allowing to calculate it for full exceptional collections with vanishing Ext^k groups for k > 1. Finally, we use it to describe an example of a non-commutative deformation of certain rational surfaces.
<]]>- FlatWrite comment View comments
http://www.ncatlab.org/nlab/show/flat+functor
See http://ncatlab.org/nlab/show/flat+morphism for notions of flatness and link to flatness in derived algebraic geometry.
http://mathoverflow.net/questions/51095/flat-module-and-torsion-free-module
In the intro to the Soulé et al Arakelov book, there is an explicit description of what flatness means for an arithmetic scheme.
<]]>- FoliationWrite comment View comments
See Foliations folder in Geometry, in particular maybe the two books by Candel and Conlon.
<]]>- FontaineWrite comment View comments
- <]]>
- Fontaine ringsWrite comment View comments
See Galois Cohomology of Fontaine rings, in Fontaine theory folder
http://mathoverflow.net/questions/70262/is-there-a-trianguline-period-ring-or-is-one-expected
http://mathoverflow.net/questions/54708/period-rings-for-galois-representations
<]]>- Fontaine-Mazur conjectureWrite comment View comments
arXiv:0907.3427 Even Galois Representations and the Fontaine-Mazur Conjecture from arXiv Front: math.NT by Frank Calegari We prove some cases of the Fontaine-Mazur conjecture for even Galois representations. In particular, we prove, under mild hypotheses, that there are no irreducible two-dimensional ordinary even Galois representations of $\Gal(\Qbar/\Q)$ with distinct Hodge-Tate weights. If $K/\Q$ is an imaginary quadratic field, we also prove (again, under certain hypotheses) that $\Gal(\Qbar/K)$ does not admit irreducible two-dimensional ordinary Galois representations of non-parallel weight. Finally, we prove that any weakly compatible family of two dimensional irreducible Galois representations of $\Gal(\Qbar/\Q)$ is, up to twist, either modular or finite.
<]]>- Formal groupWrite comment View comments
Excellent notes by Strickland
There is some good material in the green book
See Kedlaya notes also, on one of his course pages.
Yoshida: a proof of local CFT
Lazard: Bourbaki exp 76
Bondarko has a number of papers on formal groups, for example a paper completely classifying formal groups over rings of integers in local fields.
LNM0074 Frohlich. Chapters on Lie theory, Commutative FGs of dim one, Comm FGs of dim one over a DVR.
Loday on the operad of associative algebras with derivations, formal group laws, and more http://arxiv.org/abs/0906.4730
<]]>- Formal group lawsWrite comment View comments
http://mathoverflow.net/questions/5166/ravenels-question-on-mu-construction-by-formal-group-laws Nice answers!!
http://mathoverflow.net/questions/52241/formal-group-laws-and-l-series
Voevodsky's Nordfjordeid lecture - supernice (Voevodsky folder). Working over a field unfortunately. Basic constructions, of SH etc. Brief discussion of Thom spaces and homotopy purity. Cohomology theories: the motivic EM spectrum, KGL, MGL, claim that the notions of orientation and FGLs have direct analogs for P1-spectra. The slice filtration (great intro), update on Open problems paper. The zero-th slice of the unit spectrum is HZ, this is known for fields of char zero. Brief discussion of AHSS. Appendix on the Nisnevich topology, Nisnevich descent, and model structures.
Up-to-date survey article by Victor Buchstaber entitled "Complex cobordism and formal groups", which may interest some readers of the discussion group. It is available at Russian Mathematical Surveys 67:5 891--950 (English translation by Taras Panov, latest issue);
Good explanations of basics in Lurie's stable homotopy notes
<]]>- Formal smoothnessWrite comment View comments
nlab on formally smooth morphism, see also formally smooth scheme.
I think Toen also talks about this in some articles related to algebraic stacks.
<]]>- FormalityWrite comment View comments
Felix Oprea Tanre in Homotopy theory folder: Rational htpy, formality. Note: Compact Kahler manifolds are fomal. Last chapter: Brief mention of Gelfand-Fuchs cohomology and iterated integrals. Also brief list of refs on MHSs on homotopy groups on pp366
http://mathoverflow.net/questions/13005/what-is-formal
http://www.ncatlab.org/nlab/show/formal+dg-algebra
http://mathoverflow.net/questions/32889/a-few-questions-about-kontsevich-formality
<]]>- Fourier-Mukai transformWrite comment View comments
"It is an involution on the derived category of an abelian variety, and can be used to describe all vector bundles on an elliptic curve (maybe also an AV). F-M can be used to prove the Torelli theorem."
A great reference appears to be Bartocci et al (PIM276), in Geometry-Various folder.
http://mathoverflow.net/questions/9834/heuristic-behind-the-fourier-mukai-transform
arXiv:1109.3083 Fourier-Mukai functors: a survey from arXiv Front: math.AG by Alberto Canonaco, Paolo Stellari This paper surveys some recent results about Fourier-Mukai functors. In particular, given an exact functor between the bounded derived categories of coherent sheaves on two smooth projective varieties, we deal with the question whether this functor is of Fourier-Mukai type. Several related questions are answered and many open problems are stated.
Polischuk's book on abelian varieties, see the AV folder.
The Fourier-Mukai transform is mentioned in the introduction to the March 2012 Palo Alto workshop on integral cohomology and Chow groups.
See this review of Bridgeland: Equivalences of derived cats and F-M transforms: MR1651025, and also the references in this article
Original paper by Mukai in Nagoya Math. Journal 81 (1981), at the time only for abelian varieties
<]]>- FramingsWrite comment View comments
arXiv:1103.0400 Local Framings from arXiv Front: math.AT by David Barnes, Constanze Roitzheim Framings provide a way to construct Quillen functors from simplicial sets to any given model category. A more structured set-up studies stable frames giving Quillen functors from spectra to stable model categories. We will investigate how this is compatible with Bousfield localisation to gain insight into the deeper structure of the stable homotopy category. We further show how these techniques relate to rigidity questions and how they can be used to study algebraic model categories.
<]]>- FresanWrite comment View comments
Javier Fresan
<]]>- Freudenthal suspension theoremWrite comment View comments
See Baues: Homotopy types (e), Thm 10.2, or Hatcher: Algebraic topology.
<]]>- FriedlanderWrite comment View comments
- <]]>
- Frobenius manifoldWrite comment View comments
See Manin book in Quantum stuff folder
<]]>- Fukaya categoryWrite comment View comments
Book draft by Seidel on Fukaya categories and Picard-Lefschetz theory, in Symplectic folder. First chapter covers A-infty categories.
<]]>- Function fieldsWrite comment View comments
See the Park City notes of Ulmer, and maybe other stuff in the same book.
arXiv:1101.1939 Park City lectures on elliptic curves over function fields from arXiv Front: math.AG by Douglas Ulmer These are the notes from a course of five lectures at the 2009 Park City Math Institute. The focus is on elliptic curves over function fields over finite fields. In the first three lectures, we explain the main classical results (mainly due to Tate) on the Birch and Swinnerton-Dyer conjecture in this context and its connection to the Tate conjecture about divisors on surfaces. This is preceded by a "Lecture 0" on background material. In the remaining two lectures, we discuss more recent developments on elliptic curves of large rank and constructions of explicit points in high rank situations.
<]]>- Function fields analogyWrite comment View comments
http://mathoverflow.net/questions/9984/what-does-faltings-theorem-look-like-over-function-fields
Goss' fondest hope: http://noncommutativegeometry.blogspot.com/2012/10/carlitzs-formalism-and-eulers-gamma.html
<]]>- Functional equationsWrite comment View comments
http://mathoverflow.net/questions/2040/why-are-functional-equations-important
arXiv:1001.1869 Analytic Continuation of some zeta functions from arXiv Front: math.NT by Gautami Bhowmik This is an expository paper on the meromorphic continuation of zeta functions with Euler products (for example zeta functions of groups and height zeta functions) or without (for example the Goldbach zeta function). As an application we show how a natural boundary of analytic continuation can give asymptotic results.
<]]>- Functor of pointsWrite comment View comments
See Toen Essen talk for an introduction, and conditions on a functor to be a scheme. Section 1.3 in particular.
http://ncatlab.org/nlab/show/functor+of+points
http://mathoverflow.net/questions/16832/functorial-point-of-view-of-spectrum-looking-for-reference
http://mathoverflow.net/questions/33070/functorial-point-of-view-for-formal-schemes
<]]>- Fundamental groupWrite comment View comments
Fundamental group of a topos nLab
From review of Brief an G. Faltings, in Geometric Galois actions, LMS Lecture notes 242. Outline of Groth philosophy of anabelian geometry. For anabelian schemes, the geometry of X should be determined by the profinite fundamental group, together with a homomorphism from it to the absolute Galois group of the base field. The kernel of this homomorphism is the geometric fundamental group of X, which is the completion of the topological fundamental group, in case K is a subfield of the complex numbers. The property of being anabelian should be geometric, i.e. depend only on the base change to alg closure. A connected nonsingular curve in char zero is anabelian iff its geometric fundamental group is not abelian. In char p, look at its maximal prime to p quotient instead.
Donu Arapura - Purdue University Title: Hodge structure on the fundamental group revisited. Abstract: Given a CW complex X with a map from its fundamental group to a group G, one gets a map X to K(G,1), which induces a map from the cohomology of G to X. When X is a variety, I would like to discuss a Hodge theoretic/motivic analogue of this, where G would be the group associated to the Tannakian category of variations of mixed Hodge structure/motivic sheaves on X. While I'm at it, I'd like to compare this "Hodge structure" on the fundamental group with those of Hain, Morgan, and Simpson.
<]]>- Fundamental groupoidWrite comment View comments
nLab on fundamental infinity-groupoid
nlab on covering space
Goerss-Jardine, section III.1. It is the left adjoint to a classifying space functor. The fundamental groupoid of a classifying space of a small cat is the free groupoid on that cat. A consequence is that the fundamental group of the nerve of the Q-construction of an exact cat is isomorphic to the 0th K-group of the cat.
<]]>- Fundamental groups in algebraic geometryWrite comment View comments
LNM0208 Grothendieck Murre: Tame fundamental gp etc.
Motivic fundamental group? See various things of Kim.
http://londonnumbertheory.wordpress.com/2010/05/10/fundamental-groups-are-not-galois-groups/
Fundamental groups, and also Grothendieck's section conjecture - see Kim Cambridge lecture July 09
arXiv:0908.0498 On the homotopy exact sequence for Nori's fundamental group from arXiv Front: math.AG by Hélène Esnault, Phùng Hô Hai, Eckart Viehweg Unlike Grothendieck's étale fundamental group, Nori's fundamental group does not fulfill the homotopy exact sequence in general. We give necessary and sufficient conditions which force exactness of the sequence.
arXiv:1003.3599 On the algebraic fundamental group of smooth varieties in characteristic $p>0$ from arXiv Front: math.AG by Hélène Esnault, Amit Hogadi We define an analog in characteristic $p>0$ of the proalgebraic completion of the topological fundamental group of a complex manifold.
<]]>- Fundamental lemmaWrite comment View comments
arXiv:1009.1862 The Geometric Nature of the Fundamental Lemma from arXiv Front: math.AG by David Nadler The Fundamental Lemma is a somewhat obscure combinatorial identity introduced by Robert P. Langlands as an ingredient in the theory of automorphic representations. After many years of deep contributions by mathematicians working in representation theory, number theory, algebraic geometry, and algebraic topology, a proof of the Fundamental Lemma was recently completed by Ngo Bao Chau, for which he was awarded a Fields Medal. Our aim here is to touch on some of the beautiful ideas contributing to the Fundamental Lemma and its proof. We highlight the geometric nature of the problem which allows one to attack a question in p-adic analysis with the tools of algebraic geometry.
http://front.math.ucdavis.edu/0912.4512 Cohomological statements.
<]]>