Glossary

Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other

G-infinity algebraWrite comment View comments

Mentioned in http://arxiv.org/abs/0710.4510

Mentioned here: http://www.ncatlab.org/nlab/show/homotopy+BV-algebra

<]]>

See the AMS book on several complex variables (Taylor???) for a good introduction to the classical GAGA.

Toen and Vaquie proves something about when a complex variety is algebraizable, in terms of a finiteness condition (saturatedness) on an associated dg-catégorie whose homotopy cat is the derived cat of perfect complexes on the variety. File: Toen web publ caca.pdf.

Some slider from a lecture on GAGA: File AG/Various/Lecture - presentation

http://mathoverflow.net/questions/10724/relationship-between-algebraic-and-holomorphic-differential-forms

http://mathoverflow.net/questions/17937/algebraic-de-rham-cohomology-vs-analytic-de-rham-cohomology

arXiv:1101.5123 Generalizing the GAGA Principle from arXiv Front: math.AG by Jack Hall This paper generalizes the fundamental GAGA results of Serre cite{MR0082175} in three ways---to the non-separated setting, to stacks, and to families. As an application of these results, we show that analytic compactifications of $\mathcal{M}_{g,n}$ possessing modular interpretations are algebraizable.

<]]>

Galois categoriesWrite comment View comments

Title: A Tannakian Context for Galois. http://front.math.ucdavis.edu/1110.6411 Authors: Eduardo J. Dubuc, Martin Szyld. Abstract: Strong similarities have been long observed between the Galois (Categories Galoisiennes) and the Tannaka (Categories Tannakiennes) theories of representation of groups. In this paper we construct an explicit (neutral) Tannakian context for the Galois theory of atomic topoi, and prove the equivalence between its fundamental theorems. Since the theorem is known for the Galois context, this yields, in particular, a proof of the fundamental (recognition) theorem for a new Tannakian context. This example is different from the additive cases or their generalization, where the theorem is known to hold, and where the unit of the tensor product is always an object of finite presentation, which is not the case in our context.

<]]>

Galois moduleWrite comment View comments

Bondarko has a few papers about Galois modules over local fields.

Burns is also interested in Galois modules I think

Many things by Snaith et al, for example the book Galois module structure, Fields Inst Monographs 2.

<]]>

Galois representationsWrite comment View comments

See reference list for the study group on Langlands, I think in an email from Tobias Berger

Galois rep folder under N TH

Taylor articles

Possibly of some interest: book by Snaith: Topological methods in Galois rep theory, late 80s

Strauch reference list

http://mathoverflow.net/questions/77278/introductory-text-on-galois-representations

http://mathoverflow.net/questions/2791/understanding-gal-bar-q-q

Title: Modular forms of weight one: Galois representations and dimension Authors: Denis Trotabas The present notes are the expanded and polished version of three lectures given in Stanford, concerning the analytic and arithmetic properties of weight one modular forms. The author tried to write them in a style accessible to non-analytically oriented number theoritists: in particular, some effort is made to be precise on statements involving uniformity in the parameters. On the other hand, another purpose was to provide an introduction, together with a set of references, consciously kept small, to the realm of Galois representations, for non-algebraists -- like the author. The proofs are sketched, at best, but we tried to motivate the results, and to relate them to interesting conjectures. http://arxiv.org/abs/0906.4579

[arXiv:1207.6724] Variations on a theorem of Tate fra arXiv Front: math.NT av Stefan Patrikis Let $F$ be a number field. These notes explore Galois-theoretic, automorphic, and motivic analogues and refinements of Tate's basic result that continuous projective representations $Gal(\bar{F}/F) \to PGLn(C)$ lift to $GLn(C)$. We take special interest in the interaction of this result with algebraicity (on the automorphic side) and geometricity (in the sense of Fontaine-Mazur). On the motivic side, we study refinements and generalizations of the classical Kuga-Satake construction. Some auxiliary results touch on: possible infinity-types of algebraic automorphic representations; comparison of the automorphic and Galois "Tannakian formalisms"; monodromy (independence-of-$\ell$) questions for abstract Galois representations.

<]]>

Galois theoryWrite comment View comments

Hoobler, Raymond T. Purely inseparable Galois theory. Ring theory (Proc. Oklahoma Conf., Univ. Oklahoma, Norman, Okla., 1973), pp. 207–240. Lecture Notes in Pure and Appl. Math., Vol. 7, Dekker, New York, 1974.

See Rognes for ring spectra

Book: Galois theories. Abstract stuff

<]]>

Gauge theoryWrite comment View comments

http://ncatlab.org/nlab/show/gauge+theory

http://mathoverflow.net/questions/11427/looking-for-reference-on-gauge-fields-as-connections

<]]>

GeisserWrite comment View comments

Web page

MathSciNet

arXiv

<]]>

GelfandWrite comment View comments

Collected papers, 3 vols

<]]>

Gelfand-Naimark theoremWrite comment View comments

http://www.ncatlab.org/nlab/show/Gelfand+spectrum

<]]>

Generalised JacobianWrite comment View comments

Sem Bourbaki Exp 93.

<]]>

Generalized ringWrite comment View comments

nlab entry

<]]>

Generalized schemeWrite comment View comments

nlab

<]]>

Generating hypothesisWrite comment View comments

Title: The Equivariant Generating Hypothesis Authors: Anna Marie Bohmann We state the generating hypothesis in the homotopy category of G-spectra for a compact Lie group G, and prove that if G is finite, then the generating hypothesis implies the strong generating hypothesis, just as in the non-equivariant case. We also give an explicit counterexample to the generating hypothesis in the category of rational S^1-equivariant spectra.

<]]>

Generic pointsWrite comment View comments

http://mathoverflow.net/questions/2162/what-are-the-most-important-instances-of-the-yoga-of-generic-points

<]]>

GenusWrite comment View comments

See maybe stuff by Carl McTague?

Hirzebruch: Top methods in AG. In folder AG/Various. Covers the Todd genus, and talks about RR.

<]]>

Geometric categoryWrite comment View comments

See discussion in the concept note.

http://mathoverflow.net/questions/33477/did-durovs-work-give-an-example-of-noncommutative-schemes

http://mathoverflow.net/questions/58428/basic-questions-about-stacks

See Motivic stuff blog post.

There are categories which can be viewed as geometric objects. One example is Balmer's tensor triangulated geometry, treated also in an arxiv preprint by Stevenson and Dell'Ambrogio. Another is Orlov-style geometry with derived categories of sheaves. Also: Tabuada's noncommutative motives - is this based on DG categories?

http://ncatlab.org/nlab/show/Cartan+geometry

See Operad for a more on the PROs etc hierarchy.

Toen has a notion of geometric setting in the under Spec Z paper.

Toen notion of geometric context, see his cours in the Toen web folder, definition in cours2.pdf

Various cats of motives.

Fulton and MacPherson: Categorical framework for the study of singular spaces. In Geometry-Various folder. This seems to be the original source for bivariant theories in general, with quite a lot of material.

Generalized schemes; see Durov thesis link under Field with one element

http://ncatlab.org/nlab/show/Gabriel-Rosenberg+theorem

Teleman and Simpson: De Rham's theorem for 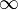Mathematical formula -stacks.

http://mathoverflow.net/questions/56833/riemannian-manifolds-etc-as-locally-ringed-spaces

http://golem.ph.utexas.edu/category/2010/06/vladimir_arnold_12_june_1937_3.html mentions Arnold's ideas on various notions of geometry

Question: Can everything be subsumed by simplicial sheaves on a site?

http://ncatlab.org/nlab/show/geometry+(for+structured+(infinity,1)-toposes) (interesting)

arXiv:1103.2139 Localization of ringed spaces from arXiv Front: math.AG by W. D. Gillam Let $X$ be a ringed space together with the data $M$ of a set $Mx$ of prime ideals of $\O{X,x}$ for each point $x \in X$. We introduce the localization of $(X,M)$, which is a locally ringed space $Y$ and a map of ringed spaces $Y \to X$ enjoying a universal property similar to the localization of a ring at a prime ideal. We use this to prove that the category of locally ringed spaces has all inverse limits, to compare them to the inverse limit in ringed spaces, and to construct a very general $\Spec$ functor. We conclude with a discussion of relative schemes.

http://mathoverflow.net/questions/84641/theme-of-isbell-duality

Demazure: Lectures on p-divisible groups. LNM302. Abstract intro to schemes, group schemes, formal schemes and more. Perhaps the reference I was really looking for is Demazure and Gabriel: Groupes algébriques. Tome I: Géométrie algébrique, généralités, groupes commutatifs.

Topological concrete category at nlab, with discussion of some terminology

nice topological space nlab

http://ncatlab.org/nlab/show/stratifold

http://nlab.mathforge.org/nlab/show/orbifold

http://ncatlab.org/nlab/show/scheme

http://nlab.mathforge.org/nlab/show/formal+scheme

arXiv:0907.3925 Compactly Generated Stacks: A Cartesian-Closed Theory of Topological Stacks from arXiv Front: math.AG by David Carchedi A convenient 2-category of topological stacks is constructed which is both complete and Cartesian closed. This 2-category, called the 2-category of compactly generated stacks, is the analogue of classical topological stacks, but for a different Grothendieck topology. In fact, there is an equivalence of 2-categories between compactly generated stacks and those classical topological stacks which admit locally compact atlases. Compactly generated stacks are also equivalent to a bicategory of topological groupoids and principal bundles, just as in the classical case. If a classical topological stack and a compactly generated stack have a presentation by the same topological groupoid, then they restrict to the same stack over locally compact Hausdorff spaces and are homotopy equivalent.

arXiv:1101.2796 A-schemes and Zariski-Riemann spaces from arXiv Front: math.AG by Satoshi Takagi In this paper, we will investigate further properties of A-schemes. The category of A-schemes possesses many properties of the category of coherent schemes, and in addition, it is co-complete and complete. There is the universal compactification, namely, the Zariski-Riemann space in the category of A-schemes. We compare it with the conventional Zariski-Riemann space, and characterize the latter by a left adjoint.

<]]>

Geometric class field theoryWrite comment View comments

http://mathoverflow.net/questions/73054/a-reference-for-geometric-class-field-theory

http://mathoverflow.net/questions/54895/geometric-abelian-class-field-theory

http://mathoverflow.net/questions/100977/how-does-one-understand-geometric-cft-in-terms-of-modularity

<]]>

Geometric invariant theoryWrite comment View comments

Book by Mumford, Fogarty and Kirwan. This and much more in folder AG/Invariant theory

<]]>

Geometric LanglandsWrite comment View comments

Check out the MO answers of Ben-Zvi, in particular discussions of how physics should tell us what to look for when generalizing to higher dimensions.

http://www.ncatlab.org/nlab/show/geometric+Langlands

http://mathoverflow.net/questions/4180/consequences-of-geometric-langlands/

Frenkel and Gross: A rigid irregular connection on the projective line http://arxiv.org/abs/0901.2163 Some kind of analogue of a family of l-adic reps.

http://mathoverflow.net/questions/56571/a-precise-statement-of-the-categorical-version-of-geometric-langlands-conjecture

<]]>

Geometric realizationWrite comment View comments

nLab

http://mathoverflow.net/questions/28380/a-canonical-and-categorical-construction-for-geometric-realization

<]]>

Geometrically unibranchWrite comment View comments

Wikipedia has an article on the def for rings.

Selected publications

Riemann-Roch theorems for higher algebraic K-theory (1981)
Universal cycle classes (1983)
Deligne homology and Abel-Jacobi maps (1984)
Homological descent for the K-theory of coherent sheaves (1984)
Intersection theory on stacks and algebraic Q-varieties (1984)
Gersten's conjecture for the K-theory of with torsion coefficients of a discrete valuation ring (1986)
K-theory and intersection theory revisited (1987)

by Gillet and Soulé:

Intersection theory using Adams operations (1987)
Descent, motives and K-theory (1996)
Filtrations on higher algebraic K-theory (1999)

<]]>

Globular objectWrite comment View comments

nLab

<]]>

Godement resolutionWrite comment View comments

Let Mathematical formula be a sheaf of abelian groups on a site with enough points. The Godement resolution of is defined as follows:

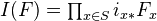
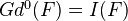
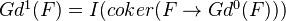
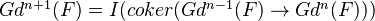
Mathematical formula

This resolution is functorial under morphisms of sites.

<]]>

GoncharovWrite comment View comments

Web page

MathSciNet

arXiv

<]]>

Goodwillie calculusWrite comment View comments

See introductory notes by Dundas

Kuhn: Goodwillie towers and chromatic homotopy: an overview

See also the original papers of Goodwillie.

Chromotopy has at least one or two blog basic blog posts.

http://ncatlab.org/nlab/show/Goodwillie+calculus

arXiv:1005.1698 Introduction to the manifold calculus of Goodwillie-Weiss from arXiv Front: math.AT by Brian A. Munson We present an introduction to the manifold calculus of functors, due to Goodwillie and Weiss. Our perspective focuses on the role the derivatives of a functor F play in this theory, and the analogies with ordinary calculus. We survey the construction of polynomial functors, the classification of homogeneous functors, and results regarding convergence of the Taylor tower. We sprinkle examples throughout, and pay special attention to spaces of smooth embeddings.

<]]>

Grading of cohomology theoriesWrite comment View comments

Why are theories in AG bigraded?? Two spheres in motivic homotopy theory? Something to do with grading of K-theory? Here is an MO question discussing the Brauer grading of K-theory and Bott periodicity, in topology: http://mathoverflow.net/questions/87345/brauer-groups-and-k-theory

<]]>

GriffithsWrite comment View comments

See his Selected Works volumes, 4 volumes.

MathSciNet

<]]>

Groebner basesWrite comment View comments

Gröbner bases: Introduction to Gröbner bases by Cox, in some book, no el copy. Also the 2 books by Cox et al (el)

preprint on a more abstract notion

<]]>

Gromov-Witten invariantsWrite comment View comments

Toen: On motives for DM stacks. Discusses Chow rings and Chow motives, 2 different defs. Motivation: Gromov-Witten invariants.

http://nlab.mathforge.org/nlab/show/Gromov-Witten+invariants

http://mathoverflow.net/questions/1312/gromov-witten-theory-and-compactifications-of-the-moduli-of-curves

A seminar

Some notes are in folder AG/Various/Gromov-Witten inv

<]]>

Grothendick constructionWrite comment View comments

Tamaki on the Grothendieck construction and enriched cats. http://front.math.ucdavis.edu/0907.0061

See nlab

<]]>

GrothendieckWrite comment View comments

The Grothendieck circle

FGA EGA SGA english index

A short Grothendieck biography: Part I and Part 2

Most of his publications including EGA, are online at NUMDAM. For SGA, see here. For SGA1 and SGA2, see also the LaTeXed versions at arXiv. For SGA3, see Gille and Polo

Lots of scans of Grothendieck writings, including Tohoku, Pursuing stacks, various letters on motives, and Recoltes et Semailles.

See also Joyal: A letter to A. Grothendieck (1984)

A. Grothendieck, Techniques de descente et Th´eor`emes d’existence en G´eom´etrie Alg´ebrique, expos´es dans le S´eminaire Bourbaki entre 1959 et 1962.

http://ncatlab.org/nlab/show/EGA

Publications:

The cohomology theory of abstract algebraic varieties pdf

<]]>

Grothendieck categoryWrite comment View comments

An abelian U-category is called Grothendieck if it admits a generator and U-small inductive limits, and U-small filtrant inductive limits are exact.

Thm: A Grothendieck category has enough injectives and admits an injective cogenerator.

http://ncatlab.org/nlab/show/Grothendieck+category

<]]>

Grothendieck dualityWrite comment View comments

Some work of Neeman

LNM1960: Lipman and Hashimoto: Foundations on Grothendieck duality for diagrams of schemes

<]]>

Grothendieck EsquisseWrite comment View comments

http://mathoverflow.net/questions/24900/a-sketch-of-esquisse-dun-programme

<]]>

Grothendieck existenceWrite comment View comments

http://ncatlab.org/nlab/show/Grothendieck+existence

<]]>

Grothendieck groupWrite comment View comments

http://www.ncatlab.org/nlab/show/Grothendieck+group good entry

References: - Hartshorne appendix A - Manin: Lectures on the K-functor - Borel and Serre: Le thm de R-R (1958)

<]]>

Grothendieck pairingWrite comment View comments

arXiv:0909.4425 Reduction of Abelian Varieties and Grothendieck's Pairing from arXiv Front: math.AG by Klaus Loerke We prove that abelian varieties of small dimension over discrete valuated, stricty henselian ground fields with perfect residue class field obtain semistable reduction after a tamely ramified extension of the ground field. Using this result we obtain perfectness results for Grothendieck's pairing.

<]]>

Grothendieck ringWrite comment View comments

For the Grothendieck ring of higher Artin stacks, see Toen: Anneaux de Grothendieck etc, file Toen web prepr K-champ.pdf. For special Artin stacks, he shows by comparing this ring to the ordinary Grothendieck ring of varieties, that invariants such as Hodge numbers and Euler characteristics (l-adic and motivic) extend uniquely to special Artin stacks. In particular, get Lefschetz trace formula for such stacks.

http://ncatlab.org/nlab/show/Grothendieck+ring

http://mathoverflow.net/questions/74433/definition-of-a-grothendieck-ring

<]]>

Grothendieck section conjectureWrite comment View comments

Minyong Kim July 09 presentation is an excellent intro to the section conj (this is maybe the same as his Cambridge lecture).

See Toen AIM talk on Homotopy types of algebraic varieties. In the last section he discusses a nonabelian Abel-Jacobi map, but it looks different from the map usually appearing the section conjecture. What is the relation? Toen says that his conjecture can be viewed as a generalization to higher-dimensional varieties.

<]]>

Grothendieck spectral sequenceWrite comment View comments

http://mathoverflow.net/questions/24143/composing-left-and-right-derived-functors

<]]>

Grothendieck topologyWrite comment View comments

One reason for introducing topologies is that one wants a coequalizer 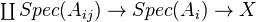Mathematical formula This doesn't exist in Aff, and the thing you get in presheaves does not behave as it should. Therefore need to take the presheaf coequalizer and sheafify it. Problem: It is not obvious which topology to take - the canonical topology is hard to get your hands on.

http://mathoverflow.net/questions/71893/cohomological-dimension-for-coarser-finer-topologies

de Jong on comparing topologies

There are lots of insights on Grothendieck topologies in general, and h and qfh in particular, in Voevodsky's thesis. I think Homology of schemes I is essentially an improved version of the thesis.

As pointed out by Peter, and also indicated by Voevodsky, one can think of a Grothendieck topology as something corresponding to fixing some colimits which should be preserved under the Yoneda embedding. Some explanation: Take a colimit diagram in the small cat, embed it under Yoneda, might get a new colimit, and a map from the new to the old. Localize by making these maps isomorphisms. Peter thinks: Every left exact localization should correspond to a Groth top.

See Anel factorization systems, and Lurie's discussion on localization, for two alternative ways of thinking of Groth topologies.

Remark: As seen for example in Toen, some topologies can be defined formally, while others need some real AG input.

Voevodsky: Homotopy theory of simplicial sheaves in cd topologies. Discusses two approaches to model structures on simplicial sheaves, Jardine-Joyal being very general, and Brown-Gersten more managable with better finiteness properties (finitely generated), but working only on certain sites associated to "cd-structures". Notions of complete, bounded and regular cd-structure.

See also the various pages on different types of sheaf cohomology.

See also Sheaf theory and similar entries under S.

References:

Shatz article, for cohomological dimension.

nLab, see also sieve

http://nlab.mathforge.org/nlab/show/Grothendieck+pretopology

http://ncatlab.org/nlab/show/Verdier+site

http://mathoverflow.net/questions/9571/canonical-topology-on-the-category-of-schemes

See Toen Essen talk section 4.3 and later, for the right way of defining Grothendieck tops on model categories, taking into account the model structure.

For abstract defs of flat, smooth and etale morphisms, see Toen Barcelona lectures.

Toen and Vaquie: Under Spec Z. Some notes: Idea: Relative alg geom. Think of commutative monoids in a symm monoidal cat C as models for affine schemes relative to C. If there is a reasonable symmetric monoidal functor from C to Z-modules, get a base change functor, and a notion of scheme under Spec(Z). Homotopical version of this requires C to have a model structure. Now have flat and Zariski topology. Can make sense of schemes: a functor with a Zariski covering. Stuff about toric varieties and GL. Brave new AG over the sphere spectrum, and the spectrum with one element. Digression: Flat and Zariski ok. For etale (and maybe hence Nisnevich), Peter Arndt said there might be three ways of doing it: by a lifting property, by factorization systems (Anel), or by mimicking something Deitmar does for monoids, see Peter's thesis in progress, and see also the notion of formally etale.

A Grothendieck topology is a standard tool for constructing cohomology theories in algebraic geometry. See Wikipedia page for basic definitions: sieves, covering families, subcanonical topology, presheaf and sheaf with values in a category with products. More serious references include Tamme: Etale cohomology, Artin lecture notes (el), and SGA4.

Grothendieck topologies are used to define various kinds of Sheaf cohomology

A morphism of topologies

The command "\\" may only appear inside a "\begin ... \end" block

T \\\\\\\\to T\\\\\\\'

is a functor on the underlying categories which take covering families to covering families and \\\\"commutes with fiber products\\\\".

Here is something about the primitive topology by Walker.

de Jong on Comparing topologies

Examples

http://mathoverflow.net/questions/74549/a-bestiary-of-topologies-on-sch

The separated étale site

Objects are required to be separated, étale, and of finite type, rather than just the last two. Cohomology is canonically IMic to étale cohomology, but and advantage is that if Mathematical formula is separated, Noetherian and regular, and

The command "\\" may only appear inside a "\begin ... \end" block

V \\\\\\\\to X

is an object, then Mathematical formula

is also separated, Noetherian and regular. Ref: Jardine, Generalized étale cohomology, p. 278.

Lisse-etale

http://mathoverflow.net/questions/53563/why-is-lack-of-functoriality-of-the-lisse-etale-topology-specific-to-the-lisse-et

The big and small fppf site

Wikipedia

The big and small fpqc site

Wikipedia

http://mathoverflow.net/questions/39211/open-faithfully-flat-morphisms-are-fpqc

The qfh topology

The h topology

Geisser\\\\'s eh topology

Kahn in K-theory handbook says something about base change thm between étale and cdh topology, see page 384 bottom.

The cdh topology

We want to talk about singular schemes which admit resolutions by smooth schemes. For this purpose we introduce the cdh topology on Mathematical formula (schemes of finite type over ). This is the minimal Grothendieck topology for which Nisnevich coverings are coverings, and also proper surjective morphisms of the following type:

The command "\\" may only appear inside a "\begin ... \end" block

W \\\\\\\\coprod U_1 \\\\\\\\to U

where

The command "\\" may only appear inside a "\begin ... \end" block

U_1 \\\\\\\\to U

is a closed embedding and

The command "\\" may only appear inside a "\begin ... \end" block

p^{-1}(U-U_1) \\\\\\\\to (U-U_1)

is an isomorphism.

Examples in FGA?

The canonical topology

On any category (with products, I guess), we can define the canonical topology, by taking as coverings the collection of all families

The command "\\" may only appear inside a "\begin ... \end" block

\\\\\\\\{U_i \\\\\\\\to U \\\\\\\\}

of universal effective epimorphisms. On this topology, every presheaf of sets is a sheaf, and it is the finest topology with this property.

The perfect site

See Milne: Arithmetic duality theorems

The smooth site

Milne again.

The positive topology

See Schmidt

The canonical topology

Def by all representables being sheaves?

The alteration topology with variants

See Gabber\\\\'s abstract from IHES talk 2009

The cohomological descent topology

See Hodge III

Syntomic topology

See Syntomic cohomology

The Zink site

See MR1803955

More Voevodsky stuff

Thesis, p 35: The p-topology and f-topology, coverings given by proper (resp finite) surjective families of morphisms.

<]]>

Grothendieck topology IIWrite comment View comments

Another example: The infinitesimal site used in crystalline cohomology.

http://mathoverflow.net/questions/117595/points-in-sites-etale-fppf

http://mathoverflow.net/questions/39212/infima-and-suprema-of-grothendieck-topologies

http://mathoverflow.net/questions/8115/does-sheafification-preserve-sheaves-for-a-different-topology

http://mathoverflow.net/questions/14486/precise-definition-of-a-scheme-functor-of-points

http://mathoverflow.net/questions/15979/motivation-for-the-etale-topology-over-other-possibilities

http://mathoverflow.net/questions/20251/cohomology-of-sheaves-in-different-grothendieck-topologies

nlab entries: etale

arXiv:1210.0431 Topologies de Grothendieck, descente, quotients fra arXiv Front: math.AG av Sylvain Brochard In this note, we present a few existence theorems for the quotient of a scheme by the action of a group. The first two sections are devoted to Grothendieck topologies and descent theory. The third one is dealing with quotients: we first give direct and (almost) complete proofs for the main existence results of SGA 3, exposé V. Then we discuss some specific situations: the quotient of an algebraic group over a field by a subgroup, the quotient of a group by the normalizer of a smooth subgroup, and quotients of affine schemes by free actions of diagonalizable groups. From place to place, the original proofs have been slightly improved (e.g. with the use of algebraic spaces). This note grew out of lectures given by the author in the CIRM (Luminy) during the Summer School "Schémas en groupes" in 2011.

A Google Books link describing Amitsur cohomology as Cech cohomology, with some material on Groth tops.

<]]>

Grothendieck topology IIIWrite comment View comments

http://mathoverflow.net/questions/103492/grothendieck-topologies-versus-pretopologies

http://mathoverflow.net/questions/80074/commuting-grothendieck-topologies

http://mathoverflow.net/questions/34717/analytic-tools-in-algebraic-geometry

de Jong on proper hypercoverings: http://math.columbia.edu/~dejong/wordpress/?p=2190 and on cocontinuous functors: http://math.columbia.edu/~dejong/wordpress/?p=2149

Several notions of Gabber (alteration topology, etc) are explained in the book on arxiv by Illusie, Laszlo and Orgogozo on the works of Gabber.

Suslin and Voevodsky: Singular homology of abstract algebraic varieties. They also have a few pages on the qfh and h topologies and their sheaves.

Voevodsky: Unstable motivic homotopy categories in Nisnevich and cdg topologies.

Milne seems to think that a suff fine top computes the true cohomology, and a natural question is how coarse can we go and still get the same cohomology. See e.g. Levine MM section 5.2.

A site of Zink, maybe same as above. Link

Bondarko claims in an MO question, that in the setting of a closed embedding from Z to X: "we have a cartesian square of sites: Xet, Xnis, Zet, Znis, and there are also sites over the Zariski points of X in this picture".

<]]>

Grothendieck universeWrite comment View comments

nLab

http://ncatlab.org/nlab/show/universe+in+a+topos

<]]>

Grothendieck's Galois theoryWrite comment View comments

http://mathoverflow.net/questions/32418/grothendiecks-galois-theory-today

<]]>

Grothendieck's six operationsWrite comment View comments

Something about a similar setup in algebraic topology is here

Possibly "Hartshorne: Residues and duality" could be a good reference

Joseph Ayoub thesis

The six functors formalism give rise to ("all"?) spectral sequences... ???

In Voevodsky (and Deligne): Lectures on cross functors, there is a discussion of the formalism of the four Grothendieck operations. This is maybe superseded by Ayoub's work. However, the lectures have some nice brief background info on the formalism (for etale sheaves), including PD and the four kind of (co)homology, indicating where there are difficulties. There is not really any material on motivic homotopy theory, it just says that such applications will be given "later".

Memo notes from Ayoub's Asterisque volumes (314, 315)

Outline: 4 chapters, of which the first 3 are in his thesis.

2 types of applications: (A) Prove properties of general motives by "devissage" using the six operations, for example by reducing to the case of Tate motives. Schur-finiteness application. (B) Consctruction of motives and motivic cohomology classes. E.g. appl to polylogs. Remark: Applications restricted since motives over fields are not well understood, although we can reduce the study of motives over general schemes to motives over fields. In particular no motivic t-structure.

CHAPTER 1:

2-categorical preliminaries, cross functors. Abstact notion of "exchange structure" for a couple of 2-functors from a cat to a 2-cat. Extension of 2-functors. Lots of technical stuff. The end product of section 6 appears to be a construction of a cross-functor on the cat of quasi-projective S-schemes. A cross functor is four 2-functors together with four exchange structures, satisfying certain axioms. Section 7 gives for any quasi-projective S-morphism Mathematical formula , a 2-morphism 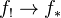, which is a 2-isomorphism if is projective. In particular, get projective base change. This stuff should simplify the proofs of fundamental theorems in SGA4, for the derived categories of etale sheaves of L-modules, where L is a finite ring.

Section 4 contains the def of stable homotopical 2-functor, from (Sch/S) to TR (cat of triangulated cats). Six axioms: Empty scheme, right adjoint, left adjoint (for smooth f), localisation, homotopy invariance, stability. The main theorem now says essentially that a stable homotopical 2-functor Mathematical formula , also denoted , can be extended, essentially uniquely, to a cross functor. I am guessing here that all the four 2-functors in the cross functor assigns the same triangulated cat to a given scheme, but a morphism between schemes is sent to the four different functors which are normally thought of as the four operations. Details in section 1.4.1.

For the generality of the scheme S, and the def of Sch/S, see section 1.3.5.

CHAPTER 2:

Many theorems in etale cohomology are proven using devissage via the proper and smooth base change theorems. Examples: (1) Constructibility of the higher direct images of constructible sheaves under a finite type morphism. (2) Stuff on cohomological dimension of the higher direct image functor (i.e. Artin's thm on affine morphisms). (3) The formalism of Verdier duality (which relies on the notion of constructible sheaf).

Want to make precise the notions of constructibility and cohomological dimension in the motivic setting as well as in the general setting of a stable homotopical 2-functor.

In order to use compacity as a notion of constructibility, it is necessary to have small sums in our triangulated cats. Therefore we use a different notion. It appears that this uses a class of objects fixed in advanced, example given in the case of SH. Similar discussion of cohomological dimension, relating to the notions of t-structure, some stuff about the homotopical t-structure on DM(k) and SH(k) for k a field.

Section 1: Background on triangulated categories. Monoidal categories, modules and projectors (aiming at the coherence problems in Verdier duality theory I think). 1.7: Discussion on various hypotheses on stable homotopical 2-functors. End of section 1: Brief intro to RoS for general schemes. Statement, known to be true for base schemes essentially of finite type over a field of char zero, conjecturally true for other schemes such as finite fields and DVRs of unequal char. Defs and basic theorems on alterations, apparently pre-Gabber.

Section 2: Analogues of the contstructibility and cohomological dimension theorems in the etale setting. For simplicity, assume S is the spectrum of a perfect field admitting RoS. Thm: For f quasi-proj, all four functors sends constructible objects to constructibles. For cohomological dimension question (i.e. t-exactness), the situation is more complex, some detiails given.

Section 3: Verdier duality. Coherence problems, surmounted. Def of two pairings, the first of which lies behind most of the standard formulas relating the 4 operations, tensor prod and internal hom. Existence and uniqueness of dualizing objects, and consequences.

Section 4: Def of stable and homotopical algebraic derivator. Extension of the 2-functor SH to an algebraic derivator. Vanishing cycles in the setting of a stable and homotopical algebraic derivator, I think DM and SH are special cases.

CHAPTER 3: Nearby cycles in the motivic setting.

Could work with the specific stable homotopical 2-functors SH and DM, but prefer to work with a general algebraic derivator. Several advantages including applications to etale and Hodge theory, and compatibility with realizations, and coherence problems.

Key notion: System of specialisation. The idea seems to be the following: We start with a diagram which looks like the inclusions of the generic and closed points of a DVR, but can be much more general, call the middle "total" scheme B. Let H1 and H2 be two stable homotopical 2-functors over the "generic point" and the "closed point" respectively. Then a system of spec. from H1 to H2 is a "compatible" family of functors from H1 of the generic fiber to H2 of the special fiber; this data should be given for each scheme over B. Examples: (1) The canonical system of spec. Mathematical formula associated to a stable homotopical 2-functor on Sch/B. (2) Classical etale settting over a strictly henselian trait.

Much more, including monodromy stuff, omitted for now.

CHAPTER 4: Construction of stable homotopical 2-functors (in particular DM and SH I think)

OUTLINE:

Section 1: Model cats and stable model cats.

Section 2: Hirschorn's localisation theorem. Notion of accessibility, gives a notion of size of objects in model cats. Small object argument, cellular complexes. Model cats presented by cofibrations.

Section 3: Stabilisation of model cats, following Hovey, wrt a fixed left Quillen endofunctor. Uses the notion of F-spectra (symmetric, nonsymmetric etc). We start by studying spectra in abstract categories. Functoriality and comparison questions. Specialisation to the case where the functor is the tensor product by a cofibrant object in a symmetric monoidal model category. Def of tensor prod of symmetric spectra, and proof that stable model structure is symmetric monoidal.

Section 4: top-local model str on the cat of presheaves on a site with values in a model cat of "coeffs" which is assumed stable. Criterion for when a coninuous functor of sites induces a Quillen adjunction.

Section 5: Construction of the algebraic derivator SH. Various details, including compact generation.

Further notes from section 3:

For any unital graded monoid Phi in the cat of groups (e.g. the standard sequence of symmetric groups), and any Phi-symmetric endofunctor F, we have a notion of (F, Phi)-spectrum in an arbitrary cat C. If C is a model cat M, have notion of levelwise WE, and also: a projective cofib (injective fib) is a map satisfying the relevant lifting property wrt levelwise trivial fibs (cofibs). Under some technical hyps, including that F has a right adjoint which is accessible, get two model structures the cat of (F, Phi)-spectra, both with levelwise WEs (Prop 4.3.21). The model cats here are all presentable by cofibrations. These model structures are called the projective unstable and the injective unstable model structure. I think projective cofibs are levelwise cofibs.

Construction of Quillen adjunctions relating cats of spectra for different choices of Phi and F.

Def: A certain class R of morphisms in M, p 239, going from the (p+1)-suspension of F(X) to the p-suspension of X, for X cofibrant. Here Susp (def on p 227) is the left adjoint to Evp (notation my own).

Def: Assume M left proper, presentable by cofibrations, and that G is accessible. Def of projective stable and injective stable model structures by Bousfield localisation at the class R.

Simple description of R-local objects, looks to me like Omega-spectra. Actual def of Omega-spectra, slightly different.

The fibrant objects in the projective stable structure are the levelwise fibrant Omega-spectra.

Quillen adjunction comparison map between the stable projective structures associated to two different (F, Phi) inputs.

The up and down shifts give a Quillen endo-adjunction. wrt the projective stable structure. More comparison maps for different input data.

If (F, G) is a Quillen eq, then get a Quillen equivalence between M and (F, Phi)-spectra with the projective model structure.

Def: Symmetric element of 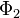Mathematical formula . A symmetric element induces a left Quillen endofunctor on (F, Phi)-spectra wrt the projective unstable and the projective stable model structures.

Thm: Assume the existence of a symmetric element. Consider the projective stable model str. Then the induced left Quillen endofunctor is in fact part of a Quillen equivalence. Also, the shift pair is a Quillen equivalence. Furthermore, these two Quillen equivalences are related by a certain natural transformation.

Another comparison theorem (4.3.40) for different input data, idea of relative symmetric element. Several substatements. Always projective stable structure it seems.

Prop 4.3.42 Comparison between levelwise projective and stable projective structures, equiv under some hyps.

Let's say GSS for (F, Phi)-spectrum. Can consider GSS objects in a cat of GSSa, have notion of biprojective bistable model structure, and compatibility relations (commutativity). (Prop 4.3.52)

More stuff about bispectra, feeding back into the proof of 4.3.40.

Paragraphe 4.3.4.Work with nonsymmetric spectra in this paragraph. Usual hyps on M. Consider a certain technical hyp (hyp56), satisfied in all cases of interest to us.

Prop 4.3.57: A certain kind of endofunctor on the levelwise homotopy cat of nonsymm spectra preserves stable equivalences.

Prop on levelwise spectra and a certain functor being a stable equivalence.

Thm: On a simple Omega-spectrum model for the R-localisation of a levelwise fibrant spectrum.

Par 4.3.5: Spectra in (unital symmetric) monoidal model cats.

For T a cofibrant object, can take F to be tensoring with T. The symmetric group acts on the n-fold tensor prod of T, and therefore we have cats of symmetric and nonsymmetric spectra SSP and SP. Some technical assumptions. We will see that SSP is a symmetric monoidal model cat (if it is stable???) and that under certain hyps, SP and SSP are Quillen equivalent.

Given a fairly general symmetric monoidal cat C, can identify symmetric spectra as left modules in Suite(Sigma,C) over a certain unital commutative algebra. Exploitation of this idea to get monoidal structure (for unstable and stable model str, under some hyps). Suff crit for SSP to be stable: I think this T should be isomorphic to a suspension in Ho(M); this is clearly true if M itself is stable.

Thm 4.3.79: Suff condition for SP and SSP to be Quillen equivalent (1) Voevodsky's 123-condition, (2) Some transfinite composition stuff, and (3) SSP is stable.

Further notes from section 4

Section 4: Model cats of sheafy nature

Goal: Explain Jardine's result on model structure on the cat of sheaves on a site. Key difference: we require the target cat to be a "cat of coeffs", in particular to be stable, so sSet is excluded.

First some presheaf theory, apparently saying that a presheaf cat is cartesian closed, under "obvious" hyps.

Def of site in terms of covering sieves, and def of sheaf. Some basic notions about sheaves.

Thm: If C is presentable, we have a sheafification functor, which commutes with finite limits.

Various properties of sheafification.

Sectino 4.4.2: Presheaves with values in a model cat.

Def of injective and projective model str (Objectwise WE, and a projective fibration is an objectwise fibration). The projective model str is cofibrantly generated if the original M was so. Same for injective str but looks much harder.

Lemma on when tensor-Hom pair gives a Quillen adjunction, nonobviuos statement, different for inj and proj.

Lemma 4.4.20 on a family of representable functors being conservative, possible useful (guessing wildly) for showing that a known functor agrees with a functor constructed by a representing object.

Cor: If the target M is stable then so is PreShv, with both model structures.

Now to Jardine's top-local model structure, in a restricted setting. Def of homotopically compact object. Def of "cat of coeffs", notably stable with homotopy category probably compactly generated. Examples: Spectra and symmetric spectra over simplicial sets, AND complexes of left R-modules, when R is any ring and the model structure is the projective one, i.e. fibrations are the surjections.

Def of 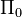Mathematical formula -sheaf ass to two objects H and K in PreShv(S, M). Def of top-local morphism in PreShv(S,M). Technical proof of the fact that we can localise at the class of top-local morphisms. Get top-local projective and injective model structures. WEs are exactly the top-local equivalences. With hyps as above, the top-local model structures are left proper and stable.

"Top-local model structure pass to the category of sheaves".

Prop: If a morphism of presheaves becomes an iso after sheafification, then it is a top-local equivalence.

Def of top-local model structure on the category of sheaves: WEs are top-local equivalences, fibrations (inj and proj) inherited from the presheaf category, cofibs by lifting property.

Elementary functoriality: Recall that a functor Mathematical formula between two sites induces 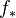on presheaves by composition; it has a left adjoint 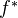. Here presheaves take values in an arbitrary complete and cocomplete cat. If the target cat is a model cat, we get a Quillen adjunction wrt the projective model structures. Also statements about morphisms of sites, and the sheaf categories. Notion of pseudo-morphism of sites. These induce Quillen adjunctions on the presheaf cats wrt the local projective model structures.

More stuff about adjunctions and about sheaves, omitted here.

Thm 4.4.60: Roughly: A pre-morphism of sites compatible with two P-structures (cf small and big sites) induces a Quillen adjunction on presheaves, wrt the projective local structures.

Monoidal stuff: under mild conditions, presheaves with values in a (symmetric) monoidal model cat inherit the structure of a (symmetric) monoidal model cat, true for various model structures.

Finally, construction of the 2-functor SH, and verification that it is a homotopical and stable algebraic derivator. Details omitted.

Just a remark on the object T, the "sphere". Bottom of p 325: We fix a projectively cofibrant object T in PreShv(Sm/S, M) such that for every smooth S-scheme U, the endofunctor 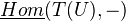Mathematical formula on M is accessible. Then towards the end (p 348) one maybe needs to assume that T is equivalent to 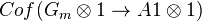, but I am not sure what the notation Cof means. For the actual construction of the 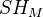(M a cat of coefficients), T should be a cofibrant presheaf with a WE to this Cof.

<]]>

Grothendieck's six opsWrite comment View comments

Something about a similar setup in algebraic topology is here

Possibly "Hartshorne: Residues and duality" could be a good reference

Joseph Ayoub thesis

The six functors formalism give rise to ("all"?) spectral sequences... ???

http://mathoverflow.net/questions/21051/why-does-the-naive-definition-of-compactly-supported-etale-cohomology-give-the-wr

http://mathoverflow.net/questions/108614/intermediate-extension-functor-exact

arXiv:1209.4020 The formalism of Grothendieck's six operations in p-adic cohomologies from arXiv Front: math.AG by Daniel Caro Let $\mathcal{V}$ be a complete discrete valued ring of mixed characteristic $(0,p)$, $K$ its field of fractions, $k$ its residue field which is supposed to be perfect. Let $X$ be a separated $k$-scheme of finite type and $Y$ be an open subscheme of $X$. We construct the category $F\text{-}D ^\mathrm{b}\mathrm{ovhol} (\mathcal{D} ^\dag{(Y,X)/K})$ of overholonomy type over $(Y,X)/K$. We check that these categories satisfy a formalism of Grothendieck's six operations.

arXiv:0908.2799 Natural Commuting of Vanishing Cycles and the Verdier Dual from arXiv Front: math.AG by David B. Massey We prove that the shifted vanishing cycles and nearby cycles commute with Verdier dualizing up to a {\bf natural} isomorphism, even when the coefficients are not in a field.

arXiv:1211.5294 Gluing restricted nerves of infinity-categories fra arXiv Front: math.AG av Yifeng Liu, Weizhe Zheng In this article, we develop a general technique for gluing subcategories of infinity-categories and prove that certain maps of simplicial sets are categorical equivalences. This applies in particular to maps naturally arising from the study of algebraic geometry, and allows us to upgrade the theory of derived categories of étale sheaves on schemes to the infinity-categorical level. In a subsequent article, we will use this technique to establish a general theory of Grothendieck's six operations for Artin stacks.

arXiv:1211.5948 Enhanced six operations and base change theorem for sheaves on Artin stacks fra arXiv Front: math.AG av Yifeng Liu, Weizhe Zheng In this article, we develop a theory of Grothendieck's six operations for lisse-étale sheaves on Artin stacks and prove all expected properties including the Base Change theorem. This extends all previous theories on this subject, including the recent one developed by Laszlo and Olsson. In particular, if we restrict ourselves to constructible sheaves, we obtain the same six operations as Laszlo and Olsson but for more general Artin stacks, with the Base Change isomorphism constructed in the derived category, and without their technical assumptions on the base scheme or on the coefficient rings. Moreover, our theory works for higher Artin stacks as well.

Our method differs from all previous approaches, as we exploit the theory of stable infinity-categories developed by Lurie. These higher categories are viewed as enhancement of usual derived categories. We introduce the infinity-categorical (co)homological descent for Cartesian sheaves and develop several infinity-categorical techniques, which, together with those in our previous article arXiv:1211.5294, allow us to handle the "homotopy coherence".

<]]>

Grothendieck-Teichmuller groupWrite comment View comments

http://mathoverflow.net/questions/40287/little-disks-operad-and-gal-bar-q-q

<]]>

GroupWrite comment View comments

http://nlab.mathforge.org/nlab/show/group

http://terrytao.wordpress.com/2009/10/19/grothendiecks-definition-of-a-group/

<]]>

Group completionWrite comment View comments

Ref Jardine-Goerss Thm 5.15 (p 255).

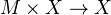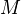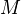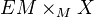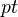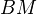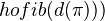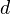Thm: Suppose that Mathematical formula is an action of a simplicial monoid on a simplicial set. Let be an abelian gp. Suppose further that the action of each vertex of induces an isomorphism in homology with A-coeffs. The the square of bisimplicial sets given by , , , is homology cartesian. This means precisely that the map from Mathematical formula to induces and iso in -homology. Here denotes the diagonal and 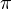is the map .

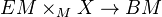Applications: Analyze the output of infinite loop space machines. Example: Each connected component of the 0th space of the 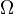Mathematical formula -spectrum corresponding to the sphere spectrum is a copy of the space given by the plus construction on the classifying space of the infinite symmetric group.

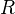Another application: Describe the K-theory spectrum associated to a ring Mathematical formula .

http://mathoverflow.net/questions/36670/group-completions-and-infinite-loop-spaces

<]]>

Group schemeWrite comment View comments

Nice review: MR0258842 on cohomological properties of group schemes, and an attempt to approach these by looking at the sheaves represented by group schemes over a general base.

Oort: LNM0015 studies some aspects of group schemes.

Various things in the Alg gps and gp schemes folder under AG.

Kevin's course on group schemes, autumn 2006: My informal course title contains the word "scheme" but you don't have to know what a scheme is to follow the course because I will be sticking to the affine case (in other words, you only have to know what a commutative ring is, and basic notions up to tensor products of modules; see e.g. Atiyah--Macdonald). I'll start by introducing the notion of a commutative affine group scheme, which is just a ring equipped with some extra structure, and will do lots of examples. Then I'll develop some of the theory from the ground up: I'll define the module of differentials and prove basic results bout it, and I'll classify finite group schemes over a perfect field. At this stage I'll either prove the necessary results from commutative algebra myself, or give precise references.

After this introductory beginning, I will then go on to the case where the base is the integers of a finite extension of Q_p and explain some subset of the following: results of Oort-Tate and Raynaud (about group schemes killed by p), results of Tate and Fontaine (about discriminants of the rings that can show up here), results of Fontaine and others about p-divisible groups when the base is not too ramified, and finally results of Breuil and others when the base is highly ramified. The course will be in the "accelerated lecture style" in the sense that at the beginning I'll assume very little and give full proofs, and then as the term goes on and I begin to panic I'll start assuming more and more of the audience.

<]]>

GroupoidWrite comment View comments

http://qchu.wordpress.com/2012/11/01/groupoids/

See Ronnie Brown

<]]>

GuletskiiWrite comment View comments

Web page

MathSciNet

arXiv

<]]>

Gysin mapWrite comment View comments

http://mathoverflow.net/questions/74181/cohomology-class-of-the-diagonal

http://mathoverflow.net/questions/53078/gysin-maps-between-smooth-schemes-generically-surjective

http://mathoverflow.net/questions/79085/gysin-maps-in-intersection-theory

arXiv:0904.4103 Gysin map and Atiyah-Hirzebruch spectral sequence from arXiv Front: math.KT by Fabio Ferrari Ruffino We discuss the relations between the Atiyah-Hirzebruch spectral sequence and the Gysin map for a multiplicative cohomology theory, on spaces having the homotopy type of a finite CW-complex. In particular, let us fix such a multiplicative cohomology theory h* and let us consider a smooth manifold X of dimension n and a compact submanifold Y of dimension p, satisfying suitable hypotheses about orientability. We prove that, starting the Atiyah-Hirzebruch spectral sequence with the Poincarè dual of Y in X, which, in our setting, is a simplicial cohomology class with coefficients in h^{n-p}(one-point), if such a class survives until the last step, it is represented by the image via the Gysin map of the unit cohomology class of Y. We then prove the analogous statement for a generic cohomology class on Y.

<]]>

Glossary

Selected publications

Examples

The big and small Zariski site

The big and small Nisnevich site

The big and small étale site

The separated étale site

Lisse-etale

The big and small fppf site

The big and small fpqc site

The qfh topology

The h topology

Geisser\\\\'s eh topology

The cdh topology

Examples in FGA?

The canonical topology

The perfect site

The smooth site

The positive topology

The canonical topology

The alteration topology with variants

The cohomological descent topology

Syntomic topology

The Zink site

More Voevodsky stuff

Memo notes from Ayoub's Asterisque volumes (314, 315)