Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- H-spaceWrite comment View comments
- <]]>
- h-topologyWrite comment View comments
Section 3 of Voevodsky's thesis is probably the earliest reference. Contains some very interesting motivation. Example which seems to show necessity of considering nonsubcanonical topologies, as well as discussion of blowups as coverings. Also mention of qfh-topology, and a long list of examples clarifying the properties of the h-topology. THen loads and loads of more interesting material, for example a comparison thm with etale cohomology, Thm 3.32: If F is a loc constant sheaf in the etale topology, then F is also an h-sheaf, and etale and h-cohomology agree.
See also Voevodsky: Homology of schemes I, which appears to be an improved version of his thesis.
Scholbach article.
On the h-topology (from Déglise's Oberwolfach talk I think): $f: W \to S$ is an h-cover if it is a topological epimorphism and remains so after any pullback (i.e. a universal topological epi). E.g. a faithfully flat map, or a proper surjective map.
<]]>- Hall algebraWrite comment View comments
Handwritten scanned notes in Toen web unpubl folder, on Hall algebras in the derived context.
Toen: Derived Hall algebras: Defines the derived Hall algebra ass to a dg-cat, which generalizes the Hall algebra of an abelian category. File Toen web publ dhall.pdf.
Bergner: Derived Hall algebras for stable homotopy theories: http://front.math.ucdavis.edu/0910.1861
<]]>- HanamuraWrite comment View comments
- <]]>
- Harish-ChandraWrite comment View comments
Collected papers, 4 volumes
<]]>- Hasse principleWrite comment View comments
arXiv:0910.2803 Hasse principles for higher-dimensional fields from arXiv Front: math.AG by Uwe Jannsen For schemes X over global or local fields, or over their rings of integers, K. Kato stated several conjectures on certain complexes of Gersten-Bloch-Ogus type, generalizing the fundamental exact sequence of Brauer groups for a global field. He proved these conjectures for low dimensions. We prove Kato's conjecture (with infinite coefficients) over number fields. In particular this gives a Hasse principle for function fields F over a number field K, involving the corresponding function fields over all completions of K. We get a conditional result over global fields K of positive characteristic, assuming resolution of singularities. This is unconditional for X of dimension at most 3, due to recent results on resolution. There are also applications to other cases considered by Kato.
<]]>- Hasse-Weil zeta functionWrite comment View comments
arXiv:1207.6177 Hasse-Weil zeta functions of SL2-character varieties of arithmetic two bridge link complements fra arXiv Front: math.NT av Shinya Harada Hasse-Weil zeta functions of SL2-character varieties of arithmetic two bridge link groups are determined.
Special values of the zeta functions at s=0,1,2 are also investigated.arXiv:1003.2451 The Langlands-Kottwitz approach for some simple Shimura Varieties from arXiv Front: math.AG by Peter Scholze We show how the Langlands-Kottwitz method can be used to determine the semisimple local factors of the Hasse-Weil zeta-function of certain Shimura varieties. On the way, we prove a conjecture of Haines and Kottwitz in this special case.
http://golem.ph.utexas.edu/category/2010/07/zeta_functions_dedekind_versus.html
<]]>- HaugsengWrite comment View comments
Rune Haugseng
<]]>- Heat kernelWrite comment View comments
Ekholm: Basic Riemannian geometry and the heat kernel
Jorgenson and Lang book: The heat kernel and theta inversion on SL2C
<]]>- HeckeWrite comment View comments
Godement: Several Bourbaki exposes on the works of Hecke
<]]>- Hecke algebraWrite comment View comments
- <]]>
- Heegner pointWrite comment View comments
Darmon and Zhang ed: Heegner points and Rankin L-series
<]]>- Height pairingWrite comment View comments
arXiv:1001.1621 The Hilbert-Polya strategy and height pairings from arXiv Front: math.AG by C. Deninger Previously we gave a conjectural cohomological argument for the validity of the Riemann hypotheses for Hasse-Weil zeta functions. In the present note we sketch how the same cohomological formalism would imply the conjectured positivity properties of the height pairings of homologically trivial cycles.
http://mathoverflow.net/questions/61620/beilinsons-height-pairing-vs-neron-tate
Bloch: Height pairings for algebraic cycles (1983). Memo notes from MR:
Let
 be a
be a 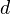 -dimensional smooth projective variety over a number field. Let
-dimensional smooth projective variety over a number field. Let 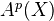 be the
be the  -VS of homologically trivial algebraic cycles of codim
-VS of homologically trivial algebraic cycles of codim 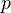 on
on  mod rational equivalence. Under certain mild assumptions, can construct height pairings
mod rational equivalence. Under certain mild assumptions, can construct height pairings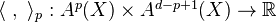
Theses generalize the Neron pairing (Neron 1965) between divisors and zero-cycles. The discriminant of the Neron pairing shows up as a regulator in the BSD conjecture. Bloch shows that the above pairing plays a similar role for the L-function associated to
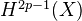 at
at 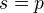 . For some evidence, see Bloch: Algebraic cycles and values of L-functions. Beilinson (Higher regulators and values of L-functions of curves; English translation exists!) has independently constructed a height pairing and regulators, conjecturally related to special values.
. For some evidence, see Bloch: Algebraic cycles and values of L-functions. Beilinson (Higher regulators and values of L-functions of curves; English translation exists!) has independently constructed a height pairing and regulators, conjecturally related to special values.The pairing above is defined as a sum of local factors over the primes of the number field. The general method uses certain homotopy-theoretic methods and properties of the spaces
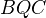 of Quillen. At the finite primes one uses the usual theory of Chern classes in etale cohomology. At the Archimedean primes, one needs a theory of Chern classes in Deligne cohomology, as constructed by Gillet.
of Quillen. At the finite primes one uses the usual theory of Chern classes in etale cohomology. At the Archimedean primes, one needs a theory of Chern classes in Deligne cohomology, as constructed by Gillet.arXiv:1103.0570 Néron's pairing and relative algebraic equivalence from arXiv Front: math.NT by Cédric Pépin Let R be a complete discrete valuation ring with algebraically closed residue field k and fraction field K. Let XK be a projective smooth and geometrically connected scheme over K. Néron defined a canonical pairing on XK between 0-cycles of degree zero and divisors which are algebraically equivalent to zero. When XK is an abelian variety, and if one restricts to those 0-cycles supported by K-rational points, Néron gave an expression of his pairing involving intersection multiplicities on the Néron model A of AK over R. When XK is a curve, Gross and Hriljac gave independantly an analogous description of Néron's pairing, but for arbitrary 0-cycles of degree zero, by means of intersection theory on a proper flat regular R-model X of XK. In this article, we show that these intersection computations are valid for an arbitrary scheme XK as above and arbitrary 0-cyles of degree zero, by using a proper flat normal and semi-factorial model X of XK over R. When XK=AK is an abelian variety, and X is a semi-factorial compactification of its Néron model A, these computations can be used to study the algebraic equivalence on X. We then obtain an interpretation of Grothentieck's duality for the Néron model A, in terms of the Picard functor of X over R.
Muller-Stach: A remark on height pairings. Contains many good references, and three different equivalent definitions!
K. Ku¨nnemann, Height pairings for algebraic cycles on abelian varieties, Annls Scient. E´c. Norm. Sup. 34(4) (2001), 503–523. MR1852008
arXiv:1001.4788 Positivity of heights of codimension 2 cycles over function field of characteristic 0 from arXiv Front: math.AG by Shou-Wu Zhang In this note, we show how the classical Hodge index theorem implies the Hodge index conjecture of Beilinson for height pairing of homologically trivial codimension two cycles over function field of characteristic 0. Such an index conjecture has been used in our paper on Gross-Schoen cycles to deduce the Bogomolov conjecture and a lower bound for Hodge class (or Faltings height) from some conjectures about metrized graphs which have just been recently proved by Zubeyir Cinkir.
2.30pm Chris Wuthrich (Nottingham). "The class group pairing on elliptic curves". Abstract: There is a pairing on the Mordell-Weil group of an elliptic curve over a number field with values in the class group of the field. It sits somewhere between the monodromy pairing and the Neron-Tate height pairing. I would like to discuss how this pairing shows up in questions on Galois module structures, how one can compute it effectively and how it links to p-descent.
arXiv:1003.0777 A generalisation of Zhang's local Gross-Zagier formula from arXiv Front: math.NT by Kathrin Maurischat On the background of Zhang's local Gross-Zagier formulae for GL(2), we study some p-adic problems. The local Gross-Zagier formulae give identities of very special local geometric data (local linking numbers) with certain local Fourier coefficients of a Rankin L-function. The local linking numbers are local coefficients of a geometric (height) pairing. The Fourier coefficients are products of the local Whittaker functions of two automorphic representations of GL(2). We establish a matching of the space of local linking numbers with the space of all those Whittaker products. Further, we construct a universally defined operator on the local linking numbers which reflects the behavior of the analytic Hecke operator. Its suitability is shown by recovering from it an equivalent of the local Gross-Zagier formulae. Our methods are throughout constructive and computational.
<]]>- HeightsWrite comment View comments
arXiv:1207.5948 An Arakelov-Theoretic Approach to Naïve Heights on Hyperelliptic Jacobians fra arXiv Front: math.NT av David Holmes We give an Arakelov-theoretic definition of a naïve height on divisors of degree zero on a hyperelliptic curve over a number field, and show that this naïve height has computably bounded difference from the Néron-Tate height of the corresponding point on the Jacobian, a key ingredient being a theorem of Faltings and Hriljac comparing the Néron-Tate height on the Jacobian to the arithmetic intersection pairing on the curve. We then use this result to give a new algorithm to compute the finite set of points on a hyperelliptic Jacobian of Néron-Tate height less than a given bound. This has applications to the problem of saturation, to the computation of integral points on hyperelliptic curves, to the use of Manin's algorithm, and for numerically testing cases of the Conjecture of Birch and Swinnerton-Dyer.
In Soulé MR1144338 there is an overview of results from Arakelov theory and a comparison of the Faltings and Philippon height, the latter based on the Chow form. Late 80s.
arXiv:0907.1458 Theta height and Faltings height from arXiv Front: math.NT by F. Pazuki Using original ideas from J.-B. Bost and S. David, we provide an explicit comparison between the Theta height and the stable Faltings height of a principally polarized abelian variety. We also give as an application an explicit upper bound on the number of K-rational points of a curve of genus g>1 over a number filed K under a conjecture of S. Lang and J. Silverman. We complete the study with a comparison between differential lattice structures.
arXiv:1001.2517 Heights and measures on analytic spaces. A survey of recent results, and some remarks from arXiv Front: math.NT by Antoine Chambert-Loir This paper has two goals. The first is to present the construction, due to the author, of measures on non-archimedean analytic varieties associated to metrized line bundles and some of its applications. We take this opportunity to add remarks, examples and mention related results.
arXiv:1004.4503 Computing Néron-Tate heights of points on hyperelliptic Jacobians from arXiv Front: math.NT by David Holmes It was shown by Faltings and Hriljac that the Néron-Tate height of a point on the Jacobian of a curve can be expressed as the self-intersection of a corresponding divisor on a regular model of the curve. We make this explicit and use it to give an algorithm for computing Néron-Tate heights on Jacobians of hyperelliptic curves. To demonstrate the practicality of our algorithm, we illustrate it by computing Néron-Tate heights on Jacobians of hyperelliptic curves of genus from 1 to 9.
<]]>- HellerWrite comment View comments
- <]]>
- Henselian ringWrite comment View comments
LNM169 Raynaud intro, looks excellent.
<]]>- Hermitian vector bundleWrite comment View comments
Chapter in Demailly in Complex Mfds folder
Appendix 4.7 of Felix, Oprea, Tanre in Homotopy th folder: Basic Hermitian and symplectic linear algebra, and basic notions of complex structures
<]]>- Higher class field theoryWrite comment View comments
Authors: Kato, Saito.
A short but nice review: MR862639 by Faltings
Maybe Shuji Saito: Some observations on motivic cohomology of arithmetic schemes
Kerz: Ideles in higher dimensions: http://front.math.ucdavis.edu/0907.5337
<]]>- Higher homotopy operationsWrite comment View comments
An interesting research proposal
<]]>- Higher local fieldWrite comment View comments
- <]]>
- Higher toposWrite comment View comments
This would usually refer to Lurie's book.
http://ncatlab.org/nlab/show/Higher+Topos+Theory
http://nlab.mathforge.org/nlab/show/models+for+infinity-stack+(infinity,1)-toposes
Toen: Segal topoi and stacks over Segal categories. File Toen web prepr msri.pdf. Analogous and in some sense equivalent to the notion of model topos, but some advantages. Includes a Giraud type statement characterizing Segal topoi among Segal cats. Notion of homotopy type of a Segal site, improving on the etale homotopy theory of schemes, and more generally on the theory of homotopy types of sites as defined by Artin and Mazur.
<]]>- Hilbert modular formsWrite comment View comments
http://mathoverflow.net/questions/55275/hilbert-modular-forms
arXiv:1102.1864 Notes on the arithmetic of Hilbert modular forms from arXiv Front: math.NT by A. Raghuram, Naomi Tanabe The purpose of this semi-expository article is to give another proof of a classical theorem of Shimura on the critical values of the standard L-function attached to a Hilbert modular form. Our proof is along the lines of previous work of Harder and Hida (independently). What is different is an organizational principle based on the period relations proved by Raghuram and Shahidi for periods attached to regular algebraic cuspidal automorphic representations. The point of view taken in this article is that one need only prove an algebraicity theorem for the most interesting L-value, namely, the central critical value of the L-function of a sufficiently general type of a cuspidal automorphic representation. The period relations mentioned above then gives us a result for all critical values. To transcribe such a result into a more classical context we also discuss the arithmetic properties of the dictionary between holomorphic Hilbert modular forms and automorphic representations of GL(2) over a totally real number field F.
<]]>- Hilbert schemeWrite comment View comments
Some notes in folder AG/Various/Hilbert sch notes
http://mathoverflow.net/questions/40161/why-do-we-care-about-the-hilbert-scheme-of-points
<]]>- HirzebruchWrite comment View comments
Collected papers, several volumes
<]]>- HistoryWrite comment View comments
- <]]>
- HKR theoremWrite comment View comments
Hochschild-Kostant-Rosenberg I think. See also Hochschild cohomology.
http://mathoverflow.net/questions/35777/hochschild-and-cyclic-homology-of-smooth-varieties
http://ncatlab.org/nlab/show/Hochschild-Kostant-Rosenberg+theorem
Toen: Algebres simplicicales etc, file Toen web prepr rhamloop.pdf. Comparison between functions on derived loop spaces and de Rham theory. Take a smooth k-algebra, k aof char zero. Then (roughly) the de Rham algebra of A and the simplical algebra
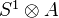 determine each other (functorial equivalence). Consequence: For a smooth k-scheme
determine each other (functorial equivalence). Consequence: For a smooth k-scheme  , the algebraic de Rham cohomology is identified with
, the algebraic de Rham cohomology is identified with 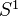 -equivariant functions on the derived loop space of
-equivariant functions on the derived loop space of  . Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]>
. Conjecturally this should follow from a more general comparison between functions on the derived loop space and cyclic homology. Also functorial and multiplicative versions of HKR type thms on decompositions of Hochschild cohomology, for any separated k-scheme.<]]>- Hochschild-Serre spectral sequenceWrite comment View comments
http://ncatlab.org/nlab/show/Hochschild-Serre+spectral+sequence
http://mathoverflow.net/questions/71663/hochschild-serre-for-hypercohomology
<]]>- Hodge conjectureWrite comment View comments
Add info also on Hodge conjecture: Lewis: A Survey of the Hodge conjecture. Deligne's Clay formulation.
http://burttotaro.wordpress.com/2012/03/18/why-believe-the-hodge-conjecture/
http://mathoverflow.net/questions/54197/why-is-the-hodge-conjecture-so-important
Can add Jossen's work as an answer here, when it appears: http://mathoverflow.net/questions/17020/why-do-people-think-that-abelian-varieties-are-the-hardest-case-for-the-hodge-con
Van Geemen: An introduction to the Hodge conjecture for abelian varieties
arXiv:0907.2503 The Hodge conjecture for self-products of certain K3 surfaces from arXiv Front: math.AG by Ulrich Schlickewei We use a result of van Geemen to determine the endomorphism algebra of the Kuga--Satake variety of a K3 surface with real multiplication. This is applied to prove the Hodge conjecture for self-products of double covers of $\PP^2$ which are ramified along six lines.
<]]>- Hodge index theoremWrite comment View comments
- <]]>
- Hodge standard conjectureWrite comment View comments
One of the two Grothendieck standard conjectures. See Kleiman in Motives.
http://mathoverflow.net/questions/27858/hodge-standard-conjecture-in-positive-characteristic
<]]>- Hodge structures on homotopy groupsWrite comment View comments
Felix Oprea Tanre in Homotopy theory folder: Rational htpy, formality. Note: Compact Kahler manifolds are fomal. Last chapter: Brief mention of Gelfand-Fuchs cohomology and iterated integrals. Also brief list of refs on MHSs on homotopy groups on pp366
<]]>- Hodge theoryWrite comment View comments
Steenbrink: A Summary of Mixed Hodge theory (in the Motives volumes)
Peters and Steenbrink: Mixed Hodge structures. Book, seems to cover everything you would want to know about MHSs.
Introduction à la théorie de Hodge: José Bertin - Jean-Pierre Demailly - Luc Illusie - Chris Peters
Deligne: Structures de Hodge mixtes reelles (in Motives vol)
Voisin books
Brylinski and Zucker: An overview of recent advances in Hodge theory (1990???)
LNM 1335: about "Hodge-Deligne theory"?
LNM 1594: Algebraic cycles and Hodge theory. Contains the following lectures:
- Green: Infinitesimal methods in Hodge theory
- Murre: Algebraic cycles and algebraic aspects of cohomology and K-theory
- Voisin: Transcendental methods in the study of algebraic cycles
- Pirola
- Van Geemen: An introduction to the Hodge conjecture for abelian varieties
- Muller-Stach: A remark on height pairings
Du Bois on something related to the Hodge filtration for singular varieties.
See everything by Steenbrink.
Toen, Katzarkov, Pantev: Schematic homotopy types and nonabelian Hodge theory. File Toen web publ nht.pdf. Constructs a "Hodge decomposition" (a certain action) on the schematic homotopy type of a smooth projective complex variety. This recovers many other Hodge invariants, short review of these.
Hodge theory computations: Cox and Batyrev in Duke 75: On the Hodge structure of projective hypersurfaces in toric varieties. Generalizes results of Griffiths and Steenbrink on Hodge str of hypersurfaces.
Brief memo notes from Deligne: Hodge II
Classical Hodge theory: The n-th singular cohomology group with coefficients in
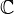 of a compact Kahler variety carries a Hodge structure of weight
of a compact Kahler variety carries a Hodge structure of weight  . We show here that the cohomology of a non-singular algebraic variety (not necessarily compact) carries a more general structure: here
. We show here that the cohomology of a non-singular algebraic variety (not necessarily compact) carries a more general structure: here 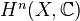 is a "successive extension" of Hodge structures of decreasing weights (in the interval
is a "successive extension" of Hodge structures of decreasing weights (in the interval 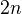 to
to  ), for which the Hodge numbers
), for which the Hodge numbers 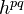 vanish for
vanish for 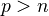 or
or 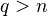 .
.The proof uses Hironaka's resolution of singularities, which allows us to "express, via a spectral sequence, the cohomology of a quasi-projective nonsingular variety in terms of the cohomology of projective nonsingular varieties".
Section 1: Filtrations. Categories of filtered objects in an abelian category. Associated graded. Induced filtrations on Hom and tensor products, and maps on Gr. Interaction between several filtrations. Bigraded object "looking like a pure Hodge structure" induces a pair of finite n-opposite filtrations, and this construction is an equivalence of cats. Notion of three filtrations being opposite, meaning that two of them induce
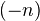 -opposite filtrations on
-opposite filtrations on 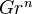 of the third. Basic theorem (1.2.10) on the (abelian!) category of objects with three opposite filtrations, in an abelian category.
of the third. Basic theorem (1.2.10) on the (abelian!) category of objects with three opposite filtrations, in an abelian category. Convention: Filtrations are decreasing unless otherwise mentioned.
Def of spectral sequence associated to a biregular filtered differential complex in an abelian category. Condition for degenaracy at
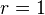 . Def of filtered qis of such things. Bifiltered diff complexes; filtrations induced by one filtration on the spectral seq of the other filtration. Various propositions on this, leading to the "lemme de deux filtrations" (Thm 1.3.16).
. Def of filtered qis of such things. Bifiltered diff complexes; filtrations induced by one filtration on the spectral seq of the other filtration. Various propositions on this, leading to the "lemme de deux filtrations" (Thm 1.3.16).Hypercohomology of filtered complexes (not using language of derived cats). All complexes assumed bounded below. Setup: Left exakt functor
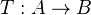 of abelian cats. For a complex
of abelian cats. For a complex 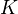 of objects in
of objects in  , def of the hypercohomology objects
, def of the hypercohomology objects 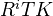 in
in 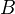 . If
. If 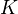 is filtered, these objects can be computed via a spectral sequence (the hypercohomology spectral sequence of the filtered complex
is filtered, these objects can be computed via a spectral sequence (the hypercohomology spectral sequence of the filtered complex 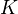 ). For example, can take the canonical or stupid filtration on any complex. Example: Leray spectral sequence for the sheaf cohomology groups
). For example, can take the canonical or stupid filtration on any complex. Example: Leray spectral sequence for the sheaf cohomology groups 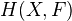 and a map
and a map 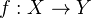 of topological spaces.
of topological spaces.Section 2: Hodge structures 2.1. Def: A real Hodge structure is a finite-dimensional real vector space
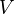 equipped with an action of the real algebraic group
equipped with an action of the real algebraic group  . Here
. Here  is the group obtained from the multiplicative group
is the group obtained from the multiplicative group 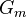 by restriction of scalars from
by restriction of scalars from 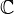 to
to 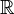 . (So the real points of
. (So the real points of  is
is 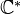 ). Such an action is equivalent to giving a bigrading of
). Such an action is equivalent to giving a bigrading of 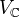 on which complex conjugation interchanges the grading indices.
on which complex conjugation interchanges the grading indices.Let
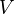 be as above. Def of weight grading on
be as above. Def of weight grading on 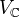 , a grading defined over the reals. Def of Hodge filtration on
, a grading defined over the reals. Def of Hodge filtration on 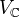 by
by 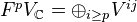 . The category of real Hodge structures is equivalent to the category of finite-dimensional real vector spaces
. The category of real Hodge structures is equivalent to the category of finite-dimensional real vector spaces 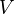 with a filtration on
with a filtration on 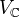 which is
which is  -opposite to its complex conjugate.
-opposite to its complex conjugate.Def: A Hodge structure of weight
 consists of an abelian group
consists of an abelian group 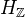 of finite type together with a real Hodge structure of weight
of finite type together with a real Hodge structure of weight  on
on 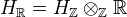 . Def of morphism. The Hodge structures of weight
. Def of morphism. The Hodge structures of weight  form an abelian category. Taking tensor products of two Hodge structures
form an abelian category. Taking tensor products of two Hodge structures 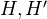 of weights
of weights  and
and 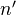 gives a Hodge structure of weight
gives a Hodge structure of weight 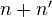 . Also, have a Hodge structure
. Also, have a Hodge structure 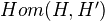 of weight
of weight 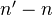 (internal Hom), exterior powers, and duals. Details on all this. Def of weight
(internal Hom), exterior powers, and duals. Details on all this. Def of weight 
 -Hodge structure, for any noetherian subring
-Hodge structure, for any noetherian subring  of the reals (replace
of the reals (replace 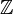 by
by  above). Def of
above). Def of  -Hodge structure, requiring that the weight grading on
-Hodge structure, requiring that the weight grading on 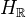 should be defined over
should be defined over 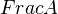 .
.Def: The Tate Hodge structure
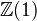 of weight
of weight 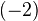 , of rank
, of rank 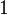 , purely of bidegree
, purely of bidegree 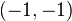 , with integral structure
, with integral structure 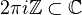 . Description of
. Description of  . Remark on choice of
. Remark on choice of  .
.Def: A polarisation of a Hodge structure
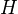 of weight
of weight  is a homomorphism
is a homomorphism  such that the real bilinear form
such that the real bilinear form 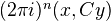 on
on 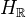 is symmetric and positive definite. Here
is symmetric and positive definite. Here  is the element of
is the element of 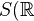 determined by a choice of
determined by a choice of 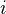 .
.Def of
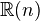 and of polarisation of real Hodge structures.
and of polarisation of real Hodge structures.2.2. Hodge theory. Let
 be a compact Kahler variety. Poincaré lemma, implying de Rham description of the complex cohomology. Hence the hypercohomology spectral sequence
be a compact Kahler variety. Poincaré lemma, implying de Rham description of the complex cohomology. Hence the hypercohomology spectral sequence 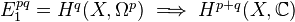 . By Hodge theory, this degenerates (
. By Hodge theory, this degenerates (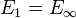 ) and the Hodge filtration on
) and the Hodge filtration on 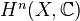 is
is  -opposite to its complex conjugate. Generalisation of this to coefficients in a local system. Can also generalise the Poincaré lemma and the hypercohomology spectral sequence (and the Hodge structure???) to the case where
-opposite to its complex conjugate. Generalisation of this to coefficients in a local system. Can also generalise the Poincaré lemma and the hypercohomology spectral sequence (and the Hodge structure???) to the case where  is complete nonsingular algebraic variety, not necessarily Kahler (use Chow's lemma and RoS, reducing to projective case).
is complete nonsingular algebraic variety, not necessarily Kahler (use Chow's lemma and RoS, reducing to projective case).Several constructions of what I think is the first Chern class of an invertible sheaf. Using this, a "trace map", and PD, we construct a map
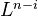 and a polarisation of the primitive part
and a polarisation of the primitive part 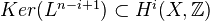 . This implies that the rational Hodge structures
. This implies that the rational Hodge structures 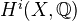 are polarisable.
are polarisable.2.3 Mixed structures. Def: A mixed Hodge structure consists of: A abelian group
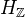 of finite type, an increasing "weight filtration"
of finite type, an increasing "weight filtration" 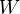 of
of 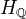 , and a (decreasing) "Hodge filtration"
, and a (decreasing) "Hodge filtration"  of
of 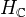 . One requires that the triple
. One requires that the triple 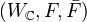 is a system of opposite filtrations.
is a system of opposite filtrations.We see that each
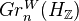 becomes a Hodge structure of weight
becomes a Hodge structure of weight  .
.Note: Every Hodge structure of weight
 defines a mixed Hodge structure in a trivial way.
defines a mixed Hodge structure in a trivial way.Thm (from thm 1.2.10): The category
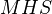 is abelian. Description of kernels and cokernels. Every morphism is strictly compatible with
is abelian. Description of kernels and cokernels. Every morphism is strictly compatible with  and
and 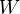 , so induces morphisms on the graded pieces. The functor
, so induces morphisms on the graded pieces. The functor 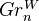 is an exact functor from
is an exact functor from  to weight
to weight 
 -Hodge structures. The functor
-Hodge structures. The functor 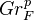 is exact.
is exact.Def: Let
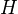 be a MHS. Define
be a MHS. Define 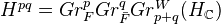 , and Hodge numbers. The Hodge number
, and Hodge numbers. The Hodge number 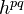 of
of 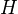 is the Hodge number of the Hodge structure
is the Hodge number of the Hodge structure 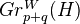
Def:
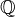 -MHS.
-MHS.Section 3: Hodge theory of nonsingular algebraic varieties.
3.1. We recall some features of log poles of holomorphic differential forms. Def of the logarithmic de Rham complex of smooth complex analytic variety
 along a normal crossings divisor
along a normal crossings divisor  . The Poincaré residue. Description of the cohomology of
. The Poincaré residue. Description of the cohomology of  as the hypercohomology of
as the hypercohomology of  with coeffs in the log de Rham complex (I think).
with coeffs in the log de Rham complex (I think). 3.2. Mixed Hodge theory. Convention: All schemes are of finite type over
 , and all sheaves are analytic.
, and all sheaves are analytic.Let
 be smooth and separated. By Nagata,
be smooth and separated. By Nagata,  is Zariski open in a complete scheme
is Zariski open in a complete scheme  . By Hironaka, one can take
. By Hironaka, one can take  to be smooth and
to be smooth and  to be a normal crossings divisor.
to be a normal crossings divisor.There are two filtrations on the log de Rham complex: Hodge and weight. Each gives rise to a spectral sequence converging to the complex cohomology of
 . Get a MHS on
. Get a MHS on 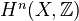 . Various lemmas on degenerating and on interaction between the filtrations. erification of functoriality and independence of choices. The above MHS is the classical weight
. Various lemmas on degenerating and on interaction between the filtrations. erification of functoriality and independence of choices. The above MHS is the classical weight  Hodge structure if
Hodge structure if  is smooth and complete. The Hodge numbers
is smooth and complete. The Hodge numbers 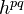 of the above MHS can be nonzero only if
of the above MHS can be nonzero only if 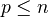 ,
, 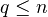 , and
, and  .
.Let
 bea meromorphic p-form on
bea meromorphic p-form on 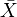 which is holomorphic on
which is holomorphic on  and with at worst log poles along
and with at worst log poles along 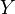 . The the restriction of
. The the restriction of  to
to  is closed, and if the cohomology class of
is closed, and if the cohomology class of  in
in  is zero, then
is zero, then 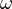 is zero.
is zero. Descriptions of the image of the cohomology of
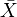 in the cohomology of
in the cohomology of  .
.Section 4: "Applications et complements".
4.1. Thm: Let
 be a smooth separated scheme, and
be a smooth separated scheme, and 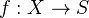 a smooth proper morphism. (i) In rational cohomology, the Leray spectral sequence
a smooth proper morphism. (i) In rational cohomology, the Leray spectral sequence 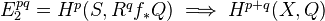 degenerates (
degenerates (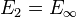 ). (ii) Let
). (ii) Let 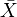 be a nonsingular compactification. Then the canonical morphism
be a nonsingular compactification. Then the canonical morphism 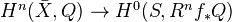 is surjective.
is surjective.In
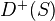 , we have
, we have 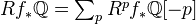 .
.Several remarks, for example: If a global section of
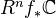 is of Hodge type
is of Hodge type  at a point, then it is so everywhere.
at a point, then it is so everywhere.4.2. The theorem of semisimplicity.
Def: Continuous family of Hodge structures on a top space
 . Various related notions. Lemma: conditions for a subcat of the category of familys of
. Various related notions. Lemma: conditions for a subcat of the category of familys of 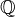 -Hodge structures to be semisimple and closed under various operations.
-Hodge structures to be semisimple and closed under various operations.Def: Algebraic family. Algebraic familys satisfy the above conditions. Some further properties of algebraic families.
Thm on semisimplicity of the representation on the fundamental group of
 given by the fiber of
given by the fiber of 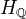 , assuming
, assuming 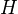 is a family belong to a subcat satisfying the conditions in the above lemma. Corollaries of this.
is a family belong to a subcat satisfying the conditions in the above lemma. Corollaries of this.4.4. Homomorphisms of abelian schemes.
Recall the description of the category of abelian
 -schemes as the category of polarisable continuous families of Hodge structures satisfying certain conditions.
-schemes as the category of polarisable continuous families of Hodge structures satisfying certain conditions.Theorem on homomorphisms of abelian schemes.
END.
Memo notes from Hodge III
Introduction: In Hodge II, we treated Hodge theory of nonsingular (not necessarily complete) varieties. Here we will treat the singular case.
In the case of a complete singular variety
 , the key idea is to use resolution of singularities to "replace"
, the key idea is to use resolution of singularities to "replace"  by a simplicial smooth projective scheme, having, in a certain sense, the same cohomology. Hence we can express the cohomology of
by a simplicial smooth projective scheme, having, in a certain sense, the same cohomology. Hence we can express the cohomology of  through a spectral sequence, in terms of the cohomology of the individual components of the simplicial scheme. Using classical Hodge theory for the components, we get a mixed Hodge structure on the cohomology of
through a spectral sequence, in terms of the cohomology of the individual components of the simplicial scheme. Using classical Hodge theory for the components, we get a mixed Hodge structure on the cohomology of  .
.For an arbitrary variety
 , we replace
, we replace  by a smooth simplicial scheme, compactified by a smooth projective simplicial scheme. The complement will be a normal crossings divisor and a union of smooth divisors. Get a mixed Hodge structure again.
by a smooth simplicial scheme, compactified by a smooth projective simplicial scheme. The complement will be a normal crossings divisor and a union of smooth divisors. Get a mixed Hodge structure again.Review of cohomological descent. Various results about vanishing of Hodge numbers. A form of Alexander duality.
We endow the cohomology of any simplicial scheme with a mixed Hodge structure. This can be applied to relative cohomology, and to cohomology of classifying spaces of algebraic groups.
The theory developed is an absolute theory (not treating
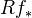 ) and only considers constant coefficients.
) and only considers constant coefficients.Convention: Schemes are of finite type over the complex numbers, and sheaves are in the complex topology.
Section 5: Cohomological descent
5.1 Simplicial topological spaces
Extremely clean summary of basic simplicial language. Def of sheaf on a simplicial topological space. The category of such sheaves form a topos, i.e. the category is equivalent to a category of sheaves on some site.
Many nontrivial definitions and details on simplicial topological spaces. Def of global sections functor (nonobvious).
5.2 Cohomology of simplicial topological spaces
Def of geometric realization of a simplicial topological space. Segal defined the cohomology of a simplicial topological space as the cohomology of the realization. Such a definition also works for K-groups. Here we adopt another definition, more suitable for sheaf techniques, namely: cohomology is given by the derived functors of the global sections functor. Here the coefficients are an abelian sheaf on the simplicial topological space. Reformulation in terms of resolutions. We have a spectral sequence
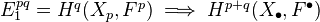 .
. Formulation in terms of derived categories, generalising the above spectral sequence.
5.3 Cohomological descent
Let
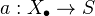 be an augmented simplicial topological space. For every sheaf
be an augmented simplicial topological space. For every sheaf  on
on  , we have an adjunction morphism
, we have an adjunction morphism 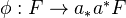 . Deriving this gives a morphism
. Deriving this gives a morphism 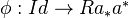 of endofunctors of
of endofunctors of 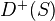 .
.Def: We say that
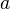 has cohomological descent if for every abelian sheaf
has cohomological descent if for every abelian sheaf  on
on  , we have
, we have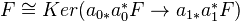
and
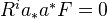
for all
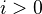 .
.I think this definition is equivalent to saying that
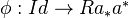 is an isomorphism.
is an isomorphism.If
 has cohomological descent, and
has cohomological descent, and  is an object of
is an object of  , the canonical map
, the canonical map 
is an isomorphism. In particular, we have a spectral sequence
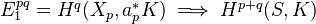
(this is hypercohomology).
Def: A continuous map
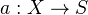 has cohomological descent if the augmentation morphism of
has cohomological descent if the augmentation morphism of 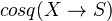 :
: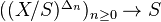
has cohomological descent. We say that
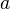 has universal cohomological descent (UCD) if, for every
has universal cohomological descent (UCD) if, for every 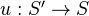 , the continuous map
, the continuous map 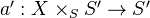 has cohomological descent.
has cohomological descent.Fundamental results, from SGA4:
- The continuous maps which have UCD form a Grothendieck topology on the category of topological spaces.
- A surjective proper morphism has UCD
- A map
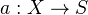 admitting sections locally on
admitting sections locally on  has UCD
has UCD - Def of k-truncated hypercovering
- Def of what it means for a map
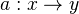 of
of  -augmented simplicial topological spaces to be a hypercovering for the UCD topology.
-augmented simplicial topological spaces to be a hypercovering for the UCD topology. - For such a hypercovering
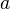 , and any
, and any 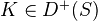 , the map
, the map 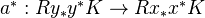 is an isomorphism.
is an isomorphism.
Example: The above recovers the Leray spectral sequence for a covering.
Def: Proper hypercovering.
Section 6: Examples of simplicial topological spaces
6.1. Classifying spaces
Details omitted for now.
6.2. Constructing hypercoverings
Details omitted for now. Come back to this later.
Def: Smooth simplicial scheme, proper simplicial scheme, divisor with normal crossings on a simplicial scheme.
Lemma: For any normal crossings divisor on a simplicial scheme, the logarithmic de Rham complexes, equipped with the weight filtration, form a filtered complex on the simplicial scheme.
We show that for every separated scheme
 over
over  , there exists (i) a smooth proper simplicial
, there exists (i) a smooth proper simplicial  -scheme, which can be taken to be s-split, (ii) a normal crossings divisor
-scheme, which can be taken to be s-split, (ii) a normal crossings divisor  in
in  ; let
; let 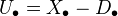 , (iii) an augmentation
, (iii) an augmentation 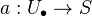 such that
such that 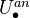 is a proper hypercovering of
is a proper hypercovering of 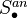 .
.6.3. Relative cohomology
Def: Let
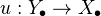 be a morphism of simplicial objects in a category
be a morphism of simplicial objects in a category 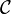 admitting finite sums and a final object
admitting finite sums and a final object  . Define the mapping cone of
. Define the mapping cone of 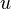 by
by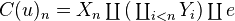
For
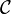 , we take the category of topological spaces, or the category of pairs consisting of a topological space and an abelian sheaf on the space. A morphism
, we take the category of topological spaces, or the category of pairs consisting of a topological space and an abelian sheaf on the space. A morphism 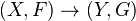 in the latter category is a continuous map
in the latter category is a continuous map 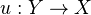 together with a
together with a 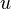 -morphism
-morphism 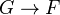 .
.Let
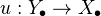 be a morphism of simplicial topological spaces, let
be a morphism of simplicial topological spaces, let  be an abelian sheaf on
be an abelian sheaf on 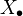 and
and  the same on
the same on 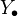 . Let
. Let 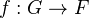 be a
be a 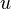 -morphism. Then the cone
-morphism. Then the cone 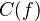 of
of  is an abelian sheaf on
is an abelian sheaf on 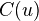 , and we define groups
, and we define groups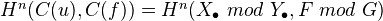
called relative cohomology groups. There is a long exact sequence:
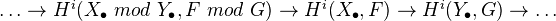
More generally, can do this for hypercohomology and complexes of sheaves (bounded below). The long exact sequence corresponds to a distinguished triangle in the derived category.
Remark: The above construction is not the only possible one.
6.4. Multisimplicial spaces
Let
 be a non-negative integer. An
be a non-negative integer. An  -simplicial object in a category
-simplicial object in a category  is a functor
is a functor 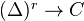 . Precomposing with the functor
. Precomposing with the functor 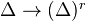 gives the associated (diagonal) simplicial object.
gives the associated (diagonal) simplicial object.Def of sheaf cohomology for an
 -simplicial topological space.
-simplicial topological space.Details on bisimplicical sets augmented towards simplicial sets; cohomological descent for this setup.
Section 7. Filtered derived category
Details omitted for now.
Section 8: Hodge theory of algebraic spaces
8.1 Hodge complexes
Many details omitted.
Prop 8.1.20: Functorial MHS on integral cohomology. Degeneration of a spectral sequence in rational cohomology. Nonvanishing of Hodge numbers only in
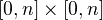 , and (I think) for the smooth case, also need
, and (I think) for the smooth case, also need 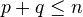 .
. 8.2 Separated algebraic spaces
Thm 8.2.4: Let
 be a separated algebraic space of finite type over
be a separated algebraic space of finite type over 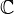 . Then teh following must hold for the pairs
. Then teh following must hold for the pairs 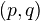 with nonvanishing Hodge numbers (for
with nonvanishing Hodge numbers (for 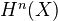 ):
):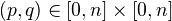
- If
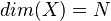 and
and 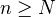 , then
, then 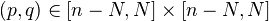
- If
 is proper, then
is proper, then 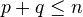
- If
 is smooth, then
is smooth, then 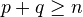
Several other interesting propositions on the behaviour of the Hodge structures on cohomology.
Kunneth isomorphisms and cup products are morphisms of mixed Hodge structures.
8.3 Hodge theory of simplicial schemes
(Or simplicial algebraic space.)
Details omitted for now. One point is that "everything" happening with cohomology groups (spectral sequence for the cohomology of a simplicial scheme, long exact sequence of relative cohomology, ...) actually respects the mixed Hodge structures.
Section 9: Examples and applications
9.1 Cohomology of linear algebraic groups.
9.2 Smooth hypersurfaces.
9.3 Constructing complexes of first order differential operators.
Corollary (Bloom and Herrera): For a quasi-projective scheme over
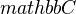 , the map
, the map 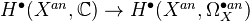 identifies the first group as a direct factor of the second.
identifies the first group as a direct factor of the second.Section 10: Hodge theory "en niveau
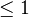 "
"10.1 1-motives
We construct an equivalence between the category of 1-motives over
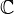 with a certain category of mixed Hodge structures.
with a certain category of mixed Hodge structures.Def: Smooth 1-motive.
Def: Hodge,
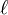 -adic and de Rham realizations of a 1-motive.
-adic and de Rham realizations of a 1-motive.10.2 1-motives and biextensions
10.3 Algebraic interpretation of mixed
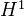 : the case of curves
: the case of curves10.4 Translation of a theorem of Picard
END
<]]>- Hodge theory classicalWrite comment View comments
http://sbseminar.wordpress.com/2011/03/23/how-to-think-about-hodge-decomposition/
Charles Siegel has many blog posts on Hodge theory
<]]>- Hodge theory generalizedWrite comment View comments
arXiv:1204.6661 Normal crossing singularities and Hodge theory over Artin rings from arXiv Front: math.AG by Christian Lehn We develop a Hodge theory for relative simple normal crossing varieties over an Artinian base scheme. We introduce the notion of a mixed Hodge structure over an Artin ring, which axiomatizes the structure that is found on the cohomology of such a variety. As an application we prove that the maps between the graded pieces of the Hodge bundles have constant rank.
<]]>- Hodge theory referencesWrite comment View comments
Green: Infinitesimal methods in Hodge theory
<]]>- Hodge-de Rham spectral sequenceWrite comment View comments
Satriano: de Rham Theory for Tame Stacks and Schemes with Linearly Reductive Singularities. About degeneration for Artin stacks in char p.
A good introduction to the degeneration assuming liftability to
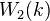 can be found in Esnault-Viehweg: Lectures on vanishing theorems. In folder AG/Various
can be found in Esnault-Viehweg: Lectures on vanishing theorems. In folder AG/Varioushttp://mathoverflow.net/questions/58834/degeneration-of-the-hodge-spectral-sequence
<]]>- Hodge-Deligne complexWrite comment View comments
For Hodge-Deligne and Hodge-Beilinson complexes, see Gelfand-Manin: Algebra V
<]]>- HollanderWrite comment View comments
- <]]>
- Homogeneous spaceWrite comment View comments
Bourbaki exp 18
Borel, Bourbaki exp 45: Cohomology of homog spaces
<]]>- Homological algebraWrite comment View comments
Many useful notes at The Rising Sea
There are some notes by Noohi from some Iranian school I think.
http://mathoverflow.net/questions/53315/references-for-sign-conventions-in-homological-algebra
For a really nice history of homological algebra, see Weibel
Standard references:
- Weibel
- Cartan and Eilenberg: Homological algebra (1956)
- Vermani (good basic introduction!)
- Grothendieck's Tohoku paper (1958?)
- S. I. Gelfand, Y. I. Manin, Methods of homological algebra, Springer-Verlag, Berlin, 1996. (other book by same authors?)
- P. Hilton, U. Stammbach, A course in homological algebra, Graduate Texts in Mathematics 4, Springer-Verlag, New York, 1997.
- MacLane: Homology
Also many other things in the Homological algebra folder
See also Spectral sequence
<]]>- HomotopicWrite comment View comments
Two maps in a model category are homotopic if they are both left and right homotopic.
<]]>- Homotopical algebraWrite comment View comments
An historical overview of homotopical algebra, by Jardine. (I have a printed copy). This could possibly be the same as his Handbook of Algebra chapter (in Various folder under ALGEBRA)
Quillen: Homotopical algebra. LNM 43 (1967)
Gelfand and Manin: Methods of homological algebra, Chapter 5.
http://www.ncatlab.org/nlab/show/homotopical+algebra
Homological algebra in homotopical language
One can say that homotopical algebra subsumes homological algebra as a special case, because of the model structure on
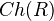 . Here are some parts of the "dictionary":
. Here are some parts of the "dictionary":- A map if rings
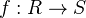 induces a Quillen adjunction, in which the left adjoint is tensoring with
induces a Quillen adjunction, in which the left adjoint is tensoring with  ("induction"), and the right adjoint is evident restriction functor. For the usual model structure, induction is a Quillen equivalance iff
("induction"), and the right adjoint is evident restriction functor. For the usual model structure, induction is a Quillen equivalance iff  is an isomorphism. For the injective model structure, induction is a Quillen equivalence iff
is an isomorphism. For the injective model structure, induction is a Quillen equivalence iff  is flat.
is flat. - A projective resolution of a module
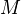 is a cofibrant replacement for
is a cofibrant replacement for 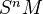 .
. - If
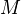 and
and 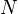 are
are 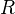 -modules, then
-modules, then 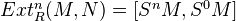 . (See here for notation.)
. (See here for notation.)
<]]>- A map if rings
- Homotopical algebraic geometryWrite comment View comments
Toen and Vezzosi: From HAG to DAG, file Toen web publ hagdag.pdf. Looks supernice, read when time!!
Toen and Vezzosi: HAG1 and HAG2. Files in Toen web publ. Lots of content.
Ref: Toen: Essen talk. Main idea: Further generalizing Relative algebraic geometry, one can replace rings by homotopy ring-like object, and get a corresponding notion of algebraic geom. More precisely, replace ring by commutative monoid in a symmetric monoidal category endowed with equivalences. Sometimes monoid here should be understood as up-to-homotopy monoid, e.g. E-infty rings. Examples include cdgas, E-inft algebras, E-infty ring spectra, and symmetric monoidal categories. See also section 5.1 for more examples including brave new algebraic geometry.
Toen and Vezzosi: Algebraic geometry over model categories. Early paper, looks very nice! Applications to interpreting DG-schemes, and to defining etale K-theory of E-infty algebras. Expectation to extend the classical work for E-infty algebras to the more general setting of AG over a model cat, for the following concepts: tangent Lie algebra, cotangent complex, Hochschild cohomology, K-theory, A-Q cohomology. Would like to do AG over a symmetric monoidal infty-cat, need strictification results. An E-infty alg should be a monoid in a SM infty-cat. Pp 34: Short nice review of operads and E-infty stuff.
Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Treats general philosophical background, various forms of homotopy theories, Segal categories, Waldhausen Kth briefly, Hochshild cohomology of Segal categories and of model cats, S-cats, Segal topoi, Tannakian duality for Segal cats, and schematic homotopy types. Also letter to May about n-cats.
<]]>- Homotopical categoryWrite comment View comments
See the book on such cats.
http://www.ncatlab.org/nlab/show/homotopical+category
See also the notions:
- Category of fibrant objects nLab, original source is Brown
- Waldhausen category
- Cofibration category nLab
- Model category (various versions, including Thomason's)
Closed monoidal homotopical cat nLab
Barwick and Kan: Partial model category.
Enriched homotopical cat nLab
<]]>- Homotopical descentWrite comment View comments
arXiv:1108.4627 The Cosmic Galois group as Koszul dual to Waldhausen's A(pt) from arXiv Front: math.AT by Jack Morava K. Hess's theory of homotopical descent, applied to the large categories of motives defined recently by Blumberg, Gepner, and Tabuada, suggests that the Koszul dual of Waldhausen's K-theory of the sphere spectrum, regarded as a supplemented algebra via the Dennis trace, plays a very general role as a kind of motivic group.
After tensoring with the rationals, the resulting Hopf algebra has close relations to the ring of quasi-symmetric functions and work of Baker and Richter on one hand, and on the other to work of Deligne and others on the motivic group for mixed Tate motives.<]]>- Homotopical invariantsWrite comment View comments
Many of these should be of the form Hom in the homotopy cat.
LNM0004 studies groups of homotopy classes, in particular homotopy classes of self-equivalences, and classes of maps from a space into a loop space. Notion of rank of a group applied, and study of homotopy commutativity.
<]]>- Homotopical mathematicsWrite comment View comments
Some people seem to think that there is some kind of paradigm shift going on in mathematics. See for example the introduction of this paper of Toen. One thing that indicates that there might be some truth in this viewpoint is that Grothendieck spent a lot of time after his public mathematical career, thinking about homotopical structures (derivateurs, stacks, ...).
Some interesting, philosophical documents:
<]]>- Homotopy algebraWrite comment View comments
- <]]>
- Homotopy cartesianWrite comment View comments
In a model category, a commutative square "X,Y,W,Z" is homotopy cartesian if for every factorization of the left map
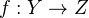 into a trivial cofibration followed by a fibration, the induced map
into a trivial cofibration followed by a fibration, the induced map 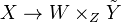 is a weak equivalence. Here
is a weak equivalence. Here 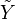 is the thing in the middle of the factorization.
is the thing in the middle of the factorization.In fact, to show that a diagram is homotopy cartesian, it suffices to find one factorization such that the relevant map is a WE.
A homotopy fibre sequence is homotopy cartesian diagram of simplicial sets, such that the lower map is the inclusion of the base point. Example: Every fibration sequence.
See Jardine-Goerss for more details, section II.9 (p 128). This section also discusses categories of cofibrant/fibrant objects.
Jardine-Goerss chapter IV discusses "detection principles" for homotopy cartesian diagrams.
<]]>- Homotopy categoryWrite comment View comments
Construction
The homotopy category
 of a model category is obtained by "inverting the WEs". One of the points of the model category axioms is that the Hom sets in the homotopy category actually are sets. The homotopy category is universal for functors from
of a model category is obtained by "inverting the WEs". One of the points of the model category axioms is that the Hom sets in the homotopy category actually are sets. The homotopy category is universal for functors from  sending WEs to isomorphisms.
sending WEs to isomorphisms.The Hom set
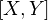 between two objects in the homotopy category is isomorphic to
between two objects in the homotopy category is isomorphic to 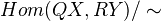 .
.Given a model category
 , the subcategory of cofibrant (fibrant, cofibrant and fibrant) objects has an equivalent homotopy category, the equivalence being induced by the inclusion functor.
, the subcategory of cofibrant (fibrant, cofibrant and fibrant) objects has an equivalent homotopy category, the equivalence being induced by the inclusion functor.For the details, the following notes are useful:
Consider maps from
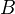 to
to  in a model category. If
in a model category. If 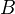 is cofibrant and
is cofibrant and  is fibrant, then the left homotopy and the right homotopy relations coincide, and are equivalence relations on the Hom set.
is fibrant, then the left homotopy and the right homotopy relations coincide, and are equivalence relations on the Hom set. Let
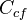 be the category of fibrant and cofibrant objects in
be the category of fibrant and cofibrant objects in  . The homotopy relation on
. The homotopy relation on 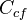 is an equivalence relation and is compatible with composition. Hence the localisation of
is an equivalence relation and is compatible with composition. Hence the localisation of  exists.
exists.A map in
 is a WE iff it is a homotopy equivalence.
is a WE iff it is a homotopy equivalence.Here is a reformulation of some of the above:
Theorem: (Hovey page 13...)
Properties
The homotopy category of a model category has all small products and coproducts.
Sometimes, the term "the homotopy category" refers to the homotopy category of topological spaces (or simplicial sets). See nLab and also the talk of Maltsiniotis in Paris Jan 2009
<]]>- Homotopy coherenceWrite comment View comments
http://www.ncatlab.org/nlab/show/homotopy+coherent+diagram
http://mathoverflow.net/questions/81721/a-homotopy-commutative-diagram-that-cannot-be-strictified
From Goerss-Jardine intro to chapter VIII: "The Dwyer-Kan theorem immediately leads to realization theorems for ho- motopy coherent diagrams in cases where the simplicial categories A model ho- motopy coherence phenomena. A realization of a homotopy coherent diagram
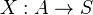 is a functor
is a functor 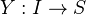 which is weakly equivalent to X in a strong sense. Insofar as the information arising from X typically consists of simplicial set maps X(α) : X(i) → X(j), one for each morphism α of I which only respect the composition laws of I up to some system of higher homotopies, a realization Y is a replacement of X, up to weak equivalence, by a collection of maps Y (α) : Y (i) → Y (j) which define a functor on the nose. Diagrams of spaces which are not quite functorial are really very common: the machines which produce the algebraic K-theory spaces, for example, are not functors (on scheme categories in particular), but they have homotopy coherent output for categorical reasons [49].
Approaches to homotopy coherence for simplicial set diagrams arising from some specific resolution constructions are discussed in Section 3; traditional ho- motopy coherence (in the sense of [90]) is one of the examples.
But more generally, we take the point of view that a homotopy coherent dia- gram on a fixed index category I is a simplicial functor X : A → S defined on any simplicial resolution A of I. We can further ask for realization results concerning homotopy coherent diagrams A → M taking values in more general simplicial model categories M. This is the subject of Section 4. We derive, in particular, realization theorems for homotopy coherent diagrams taking values in pointed simplicial sets, spectra and simplicial abelian groups (aka. chain complexes)."<]]>
which is weakly equivalent to X in a strong sense. Insofar as the information arising from X typically consists of simplicial set maps X(α) : X(i) → X(j), one for each morphism α of I which only respect the composition laws of I up to some system of higher homotopies, a realization Y is a replacement of X, up to weak equivalence, by a collection of maps Y (α) : Y (i) → Y (j) which define a functor on the nose. Diagrams of spaces which are not quite functorial are really very common: the machines which produce the algebraic K-theory spaces, for example, are not functors (on scheme categories in particular), but they have homotopy coherent output for categorical reasons [49].
Approaches to homotopy coherence for simplicial set diagrams arising from some specific resolution constructions are discussed in Section 3; traditional ho- motopy coherence (in the sense of [90]) is one of the examples.
But more generally, we take the point of view that a homotopy coherent dia- gram on a fixed index category I is a simplicial functor X : A → S defined on any simplicial resolution A of I. We can further ask for realization results concerning homotopy coherent diagrams A → M taking values in more general simplicial model categories M. This is the subject of Section 4. We derive, in particular, realization theorems for homotopy coherent diagrams taking values in pointed simplicial sets, spectra and simplicial abelian groups (aka. chain complexes)."<]]>- Homotopy colimitWrite comment View comments
Much work by Thomason. Notes from Weibel's obituary: Thomason constructed, for a diagram
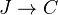 of small categories, a canonical cofibered category such that it's geometric realization is the homotopy colimit of the geometric realization of the diagram. Remark: An infinite loop space machine sends homotopy colimits in SymMonCat to the corresponding hocolims of spectra.
of small categories, a canonical cofibered category such that it's geometric realization is the homotopy colimit of the geometric realization of the diagram. Remark: An infinite loop space machine sends homotopy colimits in SymMonCat to the corresponding hocolims of spectra.arXiv:1104.0646 Realizable homotopy colimits from arXiv Front: math.AG by Beatriz Rodriguez-Gonzalez In this paper we study realizable homotopy colimits, which we define as homotopically well-behaved cofibrant approximations of colimits. Homotopical well-behavior includes cofinality, Fubini and homotopy invariance, as well as existence of pointwise homotopy left Kan extensions. We characterize such realizable homotopy colimits on (D,E) as those hocolim obtained as the composition of the simplicial replacement with a simple functor endowing (D, E) with a simplicial descent structure (arXiv:0808.3684). As an example, we deduce that (finite) homotopy limits exist for mixed Hodge complexes, and are realized through Deligne's cosimplicial construction.
http://mathoverflow.net/questions/26932/simple-examples-of-homotopy-colimits
http://mathoverflow.net/questions/33556/do-homotopy-colimits-always-commute-with-homotopy-colimits
http://mathoverflow.net/questions/33561/sequential-colim-vs-sequential-hocolim
http://mathoverflow.net/questions/55271/when-does-a-cosimplicial-object-compute-homotopy-colimits
arXiv:1109.0265 Homotopy Colimits of Algebras Over Cat-Operads and Iterated Loop Spaces from arXiv Front: math.AT by Zbigniew Fiedorowicz, Manfred Stelzer, Rainer M. Vogt We extend Thomason's homotopy colimit construction in the category of permutative categories to categories of algebras over an arbitrary $\Cat$ operad and analyze its properties. We then use this homotopy colimit to prove that the classifying space functor induces an equivalence between the category of $n$-fold monoidal categories and the category of $\mathcal{C}n$-spaces after formally inverting certain classes of weak equivalences, where $\mathcal{C}n$ is the little $n$-cubes operad. As a consequence we obtain an equivalence of the categories of $n$-fold monoidal categories and the category of $n$-fold loop spaces and loop maps after localization with respect to some other class of weak equivalences. We recover Thomason's corresponding result about infinite loop spaces and obtain related results about braided monoidal categories and 2-fold loop spaces.
Jardine-Goerss talks early in chapter IV about the homotopy colimit of a functor into simplicial sets; this hocolim is a bisimplicial set. For bisimplicial abelian groups this hocolim appears naturally "in any homology spectral sequence arising from the hocolim of a diagram of simplicial sets".
<]]>- Homotopy equivalenceWrite comment View comments
In a model category, a map
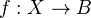 is a homotopy equivalence if there is a map in the other direction such that both compositions are homotopic to the identity.<]]>
is a homotopy equivalence if there is a map in the other direction such that both compositions are homotopic to the identity.<]]>- Homotopy groupsWrite comment View comments
We can define the homotopy groups of a fibrant simplicial set, following Hovey chapter 3.4.
Let
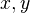 be 0-simplices in a fibrant simplicial set
be 0-simplices in a fibrant simplicial set  . Say that
. Say that 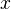 is homotopic to
is homotopic to 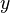 if there is a one-simplex
if there is a one-simplex 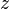 such that
such that 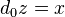 and
and 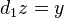 . This is an equivalence relation, and the set of equivalence classes is denoted
. This is an equivalence relation, and the set of equivalence classes is denoted 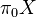 . This set is isomorphic to
. This set is isomorphic to 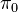 of the geometric realization. This construction is a functor from fibrant simplicial sets to sets.
of the geometric realization. This construction is a functor from fibrant simplicial sets to sets.For the other
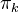 , see Hovey page 85.
, see Hovey page 85.Goerss and Schemmerhorn: One of the lessons of the last thirty years is that in order to compute homotopy classes of maps, the best strategy can be to compute the homotopy type of the mapping space, and then read off the components (p. 27). Related: The hammock localization of a category with WEs.
<]]>- Homotopy groups of spheresWrite comment View comments
Several good references, e.g. Hopkins ICM talk, the famous book.
Hatcher Spectral Seqs book draft
Hatcher AT pp 384
http://mathoverflow.net/questions/22837/what-are-the-uses-of-the-homotopy-groups-of-spheres
http://mathoverflow.net/questions/24594/survey-articles-on-homotopy-groups-of-spheres
arXiv:0910.2817 Derived functors of non-additive functors and homotopy theory from arXiv Front: math.AT by Lawrence Breen, Roman Mikhailov We develop a functorial approach to the study of the homotopy groups of spheres and Moore spaces $M(A,n)$, based on the Curtis spectral sequence and the decomposition of Lie functors as iterates of simpler functors such as the symmetric or exterior algebra functors. The discussion takes place over the integers, and includes a functorial description of the derived functors of certain Lie algebra functors, as well as of all the main cubical functors (such as the degree 3 component $SP^3$ of the symmetric algebra functor). As an illustration of this method, we retrieve in a purely algebraic manner the 3-torsion component of the homotopy groups of the 2-sphere up to degree 14, and give a unified presentation of homotopy groups $\pi_i(M(A,n))$ for small values of both $n$ and $i$.
arXiv:1009.1125 The Goodwillie tower and the EHP sequence from arXiv Front: math.AT by Mark Behrens We study the interaction between the EHP sequence and the Goodwillie tower of the identity evaluated at spheres at the prime 2. Both give rise to spectral sequences (the EHP spectral sequence and the Goodwillie spectral sequence, respectively) which compute the unstable homotopy groups of spheres. We relate the Goodwillie filtration to the P map, and the Goodwillie differentials to the H map. Furthermore, we study an iterated Atiyah-Hirzebruch spectral sequence approach to the homotopy of the layers of the Goodwillie tower of the identity on spheres. We show that differentials in these spectral sequences give rise to differentials in the EHP spectral sequence. We use our theory to re-compute the 2-primary unstable stems through the Toda range (up to the 19-stem). We also study the homological behavior of the interaction between the EHP sequence and the Goodwillie tower of the identity. This homological analysis involves the introduction of Dyer-Lashof-like operations associated to M. Ching's operad structure on the derivatives of the identity. These operations act on the mod 2 stable homology of the Goodwillie layers of any functor from spaces to spaces.
[arXiv:1108.3055] A combinatorial description of homotopy groups of spheres from arXiv Front: math.AT by Roman Mikhailov, Jie Wu We give a combinatorial description of general homotopy groups of $k$-dimensional spheres with $k\geq3$ as well as those of Moore spaces.
For $n>k\geq 3,$ we construct a finitely generated group defined by explicit generators and relations, whose center is exactly $\pi_n(S^k)$.<]]>- Homotopy invarianceWrite comment View comments
In algebraic geometry, this can mean either that a functor sends
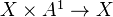 to an isomorphism, or the same statement for
to an isomorphism, or the same statement for 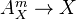 (affine m-space over
(affine m-space over  ).
).The latter statement holds for etale cohomology with torsion coeffs prime to the characteristic.
Grayson (K-th handbook p 47) mentions that there is a standard way of converting a functor into a homotopy invariant functor. Check his references to Gersten and Karoubi-Villamayor. Very briefly following Grayson: for a contravariant functor
 from a category of varieties containg the affine spaces to the category of spaces, we consider the functor
from a category of varieties containg the affine spaces to the category of spaces, we consider the functor 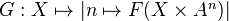 . The map
. The map 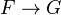 is, in a certain up-to-homotopy sense, the universal map from
is, in a certain up-to-homotopy sense, the universal map from  to a homotopy invariant functor.<]]>
to a homotopy invariant functor.<]]>- Homotopy Kan extensionWrite comment View comments
see nlab
<]]>- Homotopy limitWrite comment View comments
Thomason: The homotopy limit problem at Google books.
Shulman survey on homotopy limits and colimits
http://mathoverflow.net/questions/454/references-for-homotopy-colimit
See maybe also Weak limit and Weighted limit
A brief intro is in Toen: Essen talk, p 13.
A discussion can be found in Hovey p. 189.
The original source is probably Bousfield and Kan: Homotopy limits, completions, and localizations (Springer Lecture notes vol 304).
A good modern reference in probably the book of Hirschhorn. See also the book of Dwyer-Hirschhorn-Kan. Hirschhorn et al: Homotopy Limit Functors on Model Categories and Homotopical Categories (AMS)
Thomason: Homotopy colimits in the category of small categories.
Thomason: The homotopy limit problem
Vogt: Homotopy limits and colimits (1973)
nLab. See also limit in quasi-categories
Shulman: Homotopy limits and colimits and enriched homotopy theory arXiv
Baez on weighted colimits
A related idea might possibly be terminal object in a quasi-category
http://mathoverflow.net/questions/17425/homotopy-limits-over-fibered-categories
Dwyer: Localizations. In the Axiomatic, enriched, motivic book.
Dwyer-Spalinski in the homotopy theory folder: Model categories, Homotopy limits brief intro, localization wrt a homology theory: very brief intro on p. 54.
Goerss-Jardine p 128 introduces the holim functor as the total left derived functor
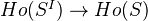 of the usual limit functor. Here
of the usual limit functor. Here  is a cofibrantly generated simplicial model cat I think. There is also a coend formula for the holim, but this should be treated in more detail elsewhere in the book.
is a cofibrantly generated simplicial model cat I think. There is also a coend formula for the holim, but this should be treated in more detail elsewhere in the book.Very brief notes from LNM0304
Bousfield and Kan: Homotopy limits, localization and completion
Want: Functorial notion of R-completion of a space X s.t.
- For
 , get under finiteness assumptions and up to homotopy, the p-profinite completion of Quillen and Sullivan
, get under finiteness assumptions and up to homotopy, the p-profinite completion of Quillen and Sullivan - For a subring of the rationals, get, up to htpy, the loclizations of Sullivan, Quillen and others.
Can define R-completion for arbitrary spaces. Need separate results on towers of fibs, cosimplicial spaces, and homotopy limits.
Usefulness: Can fracture homotopy theory into mod-p components, and construct new spaces
More on all this.
General advantages:
- Up to homotopy, R-completion preserves fibrations whenever the fundamental gp of the base acts nilpotently on the R-homology of the fibre
- Many spaces are R-good, i.e. the canonical map from X to its R-completion preserves R-homology, and is, up to homotopy, terminal among such maps
- The mod/R spectral sequence relates the R-homology of a spaces with the homotopy groups of its R-completion.
- more on Malcev completion
Now a summary of the book: See LNM304 pp4 for full version. Some highlights: A map induces iso on reduced R-homology iff it induces a homotopy equivalence between the R-completions.
Chapter 1
The R-completion is defined by first constructing a cosimplicial diagram of spaces RX, then associating with this a tower of fibrations
and finally taking the inverse limit of this tower. The R-completion comes with a natural map from X. Can think of this as the \"Artin-Mazur like completion\" in two different ways. The tower of fibs give us a spectral sequence, useful. Recover the homotopy spectral sequence with coeffs in R, as well as the unstable Adams spectral sequence, and the primitive elements in the rational cobar spectral sequence.The command "\\" may only appear inside a "\begin ... \end" block\\{ R_s X \\}Up to homotopy, the R-completion commutes with disjoint unions and finite products, and preserves multiplicative structures.
It might be the case that the homotopy groups of the R-completion are the reduced homology groups of the space, with coeffs in R. This gives an alternative view on the Hurewicz homomorphism.
Note: The R-completion of a space is fibrant because surjections are sent to fibrations.
Cont on p24
<]]>- For
- Homotopy limit IIWrite comment View comments
http://mathoverflow.net/questions/95021/homotopy-limits-of-quasi-categories
Thomason on holim: - The homotopy limit problem. In CONM19 (missing from my pdf collection I believe?)
<]]>- Homotopy pullback squareWrite comment View comments
See Hovey p. 184 for definition and properties. Or Dundas, page 39.
http://mathoverflow.net/questions/8684/homotopy-pullbacks-and-homotopy-pushouts
<]]>- Homotopy pushout squareWrite comment View comments
See Hovey p. 184 for definition and properties. Or Dundas, page 39.
<]]>- Homotopy t-structureWrite comment View comments
- <]]>
- Homotopy theory of categoriesWrite comment View comments
Thomason papers: - Cat as a closed model category - Simplicial sets from categories - Homotopy colimits in the category of small categories
I think there is a blog post from 2012 on model structure on Cat in which (unlike in Thomason's??) all objects are fibrant and cofibrant?
<]]>- Homotopy theory of homotopy theoriesWrite comment View comments
Some paper by Rezk?
arXiv:1102.0186 n-Relative Categories from arXiv Front: math.CT by C. Barwick, D. M. Kan We introduce, for every positive integer n, the notion of an n-relative category and show that the category of the small n-relative categories is a model for the homotopy theory of n-fold homotopy theories, i.e. homotopy theories of ... of homotopy theories.
<]]>- Homotopy theory of operadsWrite comment View comments
http://ncatlab.org/nlab/show/model+structure+on+operads
arXiv:1006.2316 A model structure for coloured operads in symmetric spectra from arXiv Front: math.CT by Javier J. Gutiérrez, Rainer M. Vogt We describe a model structure for coloured operads with values in the category of symmetric spectra (with the positive model structure), in which fibrations and weak equivalences are defined at the level of the underlying collections. This allows us to treat R-module spectra (where R is a cofibrant ring spectrum) as algebras over a cofibrant spectrum-valued operad with R as its first term. Using this model structure, we give suficient conditions for homotopical localizations in the category of symmetric spectra to preserve module structures.
arXiv:1002.0879 Coherence for Categorified Operadic Theories from arXiv Front: math.CT by M. R. Gould Given an algebraic theory which can be described by a (possibly symmetric) operad $P$, we propose a definition of the \emph{weakening} (or \emph{categorification}) of the theory, in which equations that hold strictly for $P$-algebras hold only up to coherent isomorphism. This generalizes the theories of monoidal categories and symmetric monoidal categories, and several related notions defined in the literature. Using this definition, we generalize the result that every monoidal category is monoidally equivalent to a strict monoidal category, and show that the "strictification" functor has an interesting universal property, being left adjoint to the forgetful functor from the category of strict $P$-categories to the category of weak $P$-categories. We further show that the categorification obtained is independent of our choice of presentation for $P$, and extend some of our results to many-sorted theories, using multicategories.
arXiv:1101.1634 Homotopy theory of non-symmetric operads from arXiv Front: math.CT by Fernando Muro We endow categories of non-symmetric operads with natural model structures. We work with no restriction on our operads and only assume the usual hypotheses for model categories with a symmetric monoidal structure. We also study categories of algebras over these operads in enriched non-symmetric monoidal model categories.
arXiv:1104.0584 Transfer of algebras over operads along derived Quillen adjunctions from arXiv Front: math.AT by Javier J. Gutiérrez Let V be a cofibrantly generated monoidal model category and let M be a monoidal V-model category. Given a cofibrant C-coloured operad P in V, we give sufficient conditions for the fibrant replacement and cofibrant replacement functors in M^C to preserve P-algebra structures. In particular, we show how P-algebra structures can be transferred along derived Quillen adjunctions of monoidal V-model categories, and we apply this result to the Quillen adjunctions defined by enriched Bousfield localizations and colocalizations on M. As an application, we prove that in the category of symmetric spectra the n-connective cover functor preserves A{\infty} and E{\infty} module spectra over connective ring spectra, for every integer n.
arXiv:1109.1004 Dendroidal sets and simplicial operads from arXiv Front: math.CT by Denis-Charles Cisinski, Ieke Moerdijk We establish a Quillen equivalence relating the homotopy theory of Segal operads and the homotopy theory of simplicial operads, from which we deduce that the homotopy coherent nerve functor is a right Quillen equivalence from the model category of simplicial operads to the model category structure for infinity-operads on the category of dendroidal sets. By slicing over the monoidal unit, this also gives the Quillen equivalence between Segal categories and simplicial categories proved by J. Bergner, as well as the Quillen equivalence between quasi-categories and simplicial categories proved by A. Joyal and J. Lurie. We also explain how this theory applies to the usual notion of operad (i.e. with a single colour) in the category of spaces.
arXiv:1209.1087 The homotopy theory of simplicial props from arXiv Front: math.AT by Philip Hackney, Marcy Robertson The category of (colored) props is an enhancement of the category of colored operads, and thus of the category of small categories. In this paper, the second in a series on "higher props," we show that the category of all small colored simplicial props admits a cofibrantly generated model category structure. With this model structure, the forgetful functor from props to operads is a right Quillen functor.
<]]>- Homotopy theory of schemesWrite comment View comments
Something on topological realization functors over
 and
and  , by Dugger and Isaksen<]]>
, by Dugger and Isaksen<]]>- Homotopy theory referencesWrite comment View comments
Whitehead: Elements of homotopy theory
<]]>- Homotopy typeWrite comment View comments
Essay topic Grojnowski
This essay is an introduction to homological and homotopical algebra. The first aim is to understand differential graded commutative algebras, which appear everywhere in characteristic zero geometry, topology, and algebra. For example, given a manifold, one can consider the algebra of differential forms on it; the main theorem of ”rational homotopy theory” is the statement that this tells you everything about the homotopy type of the manifold if you neglect torsion. The second, more ambitious goal is to understand torsion. The language of dga’s is inadequate, and the correct (homotopy invariant) notion is of ”algebras for the E1-operad”. Begin with two computations (both of which will require you learning a lot!) (1) Compute the rational homotopy of spheres, (2) Compute the homology of Eilenberg-MacLane spaces. Then understand how the deRham functor gives an equivalence of categories between topological spaces localised at Q and connected cdga’s; that is learn the rational homotopy theory of Quillen and Sullivan. This encodes the computation of (1); you can find it in various textbooks and papers. If any time remains you can aim to understand Mandell’s theorem, which is the characteristic p analogue. This requires a lot more background on homotopical algebra; a basic computational input is (2) above. References Many textbook expositions exist, now. The original papers are: [1] D. Quillen, Rational homotopy theory. Ann. of Math. 90, 1969, 205–295. [2] D. Sullivan, Infinitesimal computations in topology. Inst. Hautes Etudes Sci. Publ. Math. No. 47, (1977), 269–331. [3] M. Mandell, E1 algebras and p-adic homotopy theory, Topology 40 (2001), 43–94.
Notes from Baues: Homotopy types (e)
Homotopy types can be modeled by polyhedra, simplicial complexes, simplicial sets, singular sets of topological spaces, nerves of small cats, nerves of posets, CW complexes, simplicial groups, free simplicial groups.
n-types (vanishing higher homotopy groups), Postnikov functor from the homotopy cat of (CW?) spaces to n-types. Get sequence of functors
1-types are the same as
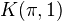 's (Eilenberg-MacLane spaces), so can be viewed as groups. More precisely,
's (Eilenberg-MacLane spaces), so can be viewed as groups. More precisely, 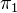 is an equiv of cats from 1-types to groups. Similarly for 2-types and (the homotopy cat of) crossed modules, and for 3-types and quadratic modules.
is an equiv of cats from 1-types to groups. Similarly for 2-types and (the homotopy cat of) crossed modules, and for 3-types and quadratic modules.Other algebraic models for homotopy types. One interesting example: The Grothendieck construction for n-types with vanishing
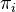 for
for  , using group cohomology.
, using group cohomology.Simply connected homotopy types and
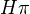 -duality: Have homotopy decompositions, using fiber sequences and Eilenberg-MacLane spaces, which constructs a homotopy type as a inverse limit. Dually, homology decomposition, using Moore spaces, cofiber sequences, and a direct limit. The homotopy decomposition can also be obtained via the Postnikov functors. Dwyer, Kan and Smith constructed a space which parameterizes all homotopy decompositions associated to a graded abelian group
-duality: Have homotopy decompositions, using fiber sequences and Eilenberg-MacLane spaces, which constructs a homotopy type as a inverse limit. Dually, homology decomposition, using Moore spaces, cofiber sequences, and a direct limit. The homotopy decomposition can also be obtained via the Postnikov functors. Dwyer, Kan and Smith constructed a space which parameterizes all homotopy decompositions associated to a graded abelian group  . Its path components corresponds to the set of homotopy types associated to this graded group. The n-th homotopy group is an equiv of cats from the relevant cat of E-M spaces to abelian groups, and there is a functor in the other direction (iterated classifying space).
. Its path components corresponds to the set of homotopy types associated to this graded group. The n-th homotopy group is an equiv of cats from the relevant cat of E-M spaces to abelian groups, and there is a functor in the other direction (iterated classifying space).  is not an eq of cats on Moore spaces, but is a detecting functor. Classes of maps between E-M spaces are by def cohomology operations; these are computable in some sense. Classes of maps between Moore spaces include homotopy groups of spheres as special examples. Def: Homotopy and cohomology groups with coeffs in a group
is not an eq of cats on Moore spaces, but is a detecting functor. Classes of maps between E-M spaces are by def cohomology operations; these are computable in some sense. Classes of maps between Moore spaces include homotopy groups of spheres as special examples. Def: Homotopy and cohomology groups with coeffs in a group  . k-invariants = Postnikov invariants, defined as certain elements in
. k-invariants = Postnikov invariants, defined as certain elements in  . Also dual notion of boundary invariant. Def of pseudo-homology, using Moore spaces, dual to singular chain def of cohomology.
. Also dual notion of boundary invariant. Def of pseudo-homology, using Moore spaces, dual to singular chain def of cohomology.The Hurewicz homomorphism, coming from applying
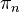 to the map from
to the map from  to the infinite symmetric product of
to the infinite symmetric product of  (whose homotopy is the homology of
(whose homotopy is the homology of  by Dold-Thom). Relation to homotopy types. Related notion of
by Dold-Thom). Relation to homotopy types. Related notion of 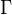 -groups (with coefficients), fitting the Hurewicz homomorphisms into a long exact sequence.
-groups (with coefficients), fitting the Hurewicz homomorphisms into a long exact sequence. Use of Postnikov and boundary invariants to classify homotopy types.
Infinite symmetric product, Dold-Thom iso.
Stable homotopy types. Properties of suspension. Algebraic models.
Some explicit examples and applications, for example allowing us to compute generalized (co)homology of 4-dimensional polyhedra in terms of the values on a small number of "prime factors".
<]]>- Homotopy type theoryWrite comment View comments
See the series of posts on n-category cafe. Ask Peter for more references.
Probably a nice introduction: http://front.math.ucdavis.edu/1210.5658
<]]>- HopfWrite comment View comments
Collected papers of H. Hopf, as well as Selected works of Eberhard Hopf, 1 volume each
<]]>- Hopf algebraWrite comment View comments
Sweedler book, in Various folder under ALGEBRA
<]]>- HopkinsWrite comment View comments
- <]]>
- HornbostelWrite comment View comments
- <]]>
- HoveyWrite comment View comments
- <]]>
- HuWrite comment View comments
- <]]>
- HuberWrite comment View comments
Selected publications:
- Mixed perverse sheaves for schemes over number fields
<]]>- HurewiczWrite comment View comments
Collected works 1 volume
<]]>- Hurewicz fibrationWrite comment View comments
See Goerss-Jardine section III.3. It says that for an n-connected Kan complex, the map from
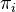 to reduced homology is an iso for
to reduced homology is an iso for  and an epi for
and an epi for 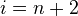 . Also relative version, and various other related things including Freudenthal.<]]>
. Also relative version, and various other related things including Freudenthal.<]]>- Hurewicz theoremWrite comment View comments
- <]]>
- Hyperbolic geometryWrite comment View comments
There is a SUMS book.
<]]>- Hypercohomology spectrumWrite comment View comments
Refs:
Thomason: Algebraic K-theory and etale cohomology
Geisser in K-theory handbook, page 213.
Briefly (go back to Geisser later): Start with a presheaf of spectra
 on some site of a scheme
on some site of a scheme  . Then the hypercohomology spectrum of
. Then the hypercohomology spectrum of  is a homotopy limit of a certain simplicial spectrum. It has an associated spectral sequence.<]]>
is a homotopy limit of a certain simplicial spectrum. It has an associated spectral sequence.<]]>- HypercoverWrite comment View comments
Not sure how this relates to Deligne's notion of hypercovering
<]]>- HypercoveringWrite comment View comments
Lurie has a discussion about hypercoverings vs coverings, and sheaves, in Higher topos theory.
Artin-Mazur LNM0100 defines hypercovering on page 96. Def: A hypercovering of a pointed site C is a pointed simplicial objects with values in the site, such that two conditions are satisfied. A hypercovering of an object X is a hypercovering of the site C/X. Example: Take C to be the site of sets, then a hypercovering is a simplicial set which is nonempty, Kan, and contractible. Some intuition explained, and some lemmas. Cor 8.15 spectral sequence ass to a hypercovering and an abelian sheaf.
Pal said a hypercovering is a simplicial object in the cat of coverings, which is Kan contractible, i.e. trivially fibrant.
<]]>