Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- k-surjectiveWrite comment View comments
See also stuff, structure, property
<]]>- K-theory handbookWrite comment View comments
The K-theory handbook is a wonderful collection of surveys. Here are links to the articles which are found online:
All articles only intended for authors!
All articles also on SpringerLink
- Carlsson: Deloopings in algebraic K-theory
<]]>- K3 surfacesWrite comment View comments
http://mathoverflow.net/questions/59347/why-does-so-much-recent-work-involve-k3-surfaces
http://mathoverflow.net/questions/107960/how-to-compute-the-picard-rank-of-a-k3-surface
arXiv:0912.5299 Chow groups and derived categories of K3 surfaces from arXiv Front: math.CT by Daniel Huybrechts This survey is based on my talk at the conference `Classical algebraic geometry today' at the MSRI. Some new results on the action of symplectomorphisms on the Chow group are added.
<]]>- Kahler manifoldWrite comment View comments
Bourbaki exp 60: Varietes localement Kahleriennes
Exp 63: Riemann-Roch for compact Kahler surfaces, after Kodaira
Various books in Complex manifolds folder
Kahler manifolds of restricted type = Kahler manifolds whose periods are integral = Hodge manifolds = complex projective variety. Ref: Kodaira, Hodge
Quote from MO: "Since all such manifolds are Kahler, we can also apply Kontsevich deformation to them to obtain a q-defomation. "
<]]>- KahnWrite comment View comments
Selected publications:
- Colliot-Thelene, Hoobler and Kahn: The Bloch-Ogus-Gabber theorem (1997)
<]]>- KanWrite comment View comments
- <]]>
- Kan complexWrite comment View comments
I think a Kan complex is a simplicial set which has the HEP wrt all inclusions of simplicial sets. It is enough to check this for the standard inclusions of horns.
Every nerve of a group is a Kan complex, but not every nerve of a category. For
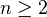 , the simplicial set
, the simplicial set 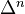 is not a Kan complex.
is not a Kan complex.From MR of Gugenheim: On supercomplexes; if
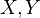 are semisimplicial complexes, and
are semisimplicial complexes, and  a subcomplex of
a subcomplex of  , then
, then 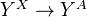 is a fibre map (warning for strange terminology).<]]>
is a fibre map (warning for strange terminology).<]]>- Kan extensionWrite comment View comments
For homotopy Kan extensions, see Dwyer et al: The A-complexity of a space
See also Kan lift in nLab
<]]>- Kan fibrationWrite comment View comments
The geometric realization of a Kan fibration is a Serre fibration. Proved by Quillen in a very short paper.
<]]>- KapranovWrite comment View comments
- <]]>
- Karoubian categoryWrite comment View comments
- <]]>
- KatoWrite comment View comments
arXiv (for some reason, this search misses the five-author paper on noncommutative Iwasawa theory, which is also on the arXiv)
Publications
- Kato and Saito: Global class field theory of arithmetic schemes
<]]>- Kato conjecturesWrite comment View comments
arXiv:0910.2803 Hasse principles for higher-dimensional fields from arXiv Front: math.AG by Uwe Jannsen For schemes X over global or local fields, or over their rings of integers, K. Kato stated several conjectures on certain complexes of Gersten-Bloch-Ogus type, generalizing the fundamental exact sequence of Brauer groups for a global field. He proved these conjectures for low dimensions. We prove Kato's conjecture (with infinite coefficients) over number fields. In particular this gives a Hasse principle for function fields F over a number field K, involving the corresponding function fields over all completions of K. We get a conditional result over global fields K of positive characteristic, assuming resolution of singularities. This is unconditional for X of dimension at most 3, due to recent results on resolution. There are also applications to other cases considered by Kato.
arXiv:0910.2815 Kato conjecture and motivic cohomology over finite fields from arXiv Front: math.AG by Uwe Jannsen, Shuji Saito For an arithmetical scheme X, K. Kato introduced a certain complex of Gersten-Bloch-Ogus type whose component in degree a involves Galois cohomology groups of the residue fields of all the points of X of dimension a. He stated a conjecture on its homology generalizing the fundamental exact sequences for Brauer groups of global fields. We prove the conjecture over a finite field assuming resolution of singularities. Thanks to a recently established result on resolution of singularities for embedded surfaces, it implies the unconditional vanishing of the homology up to degree 4 for X projective smooth over a finite field. We give an application to finiteness questions for some motivic cohomology groups over finite fields.
<]]>- KellerWrite comment View comments
- <]]>
- Ken Brown's lemmaWrite comment View comments
Let
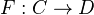 be a functor from a model category to a category
be a functor from a model category to a category 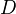 with a class of WEs satisfying (2-out-of-3). Suppose
with a class of WEs satisfying (2-out-of-3). Suppose  takes trivial cofibrations between cofibrant objects to WEs. Then
takes trivial cofibrations between cofibrant objects to WEs. Then  takes all WEs between cofibrant objects to WEs. Also dual statement.<]]>
takes all WEs between cofibrant objects to WEs. Also dual statement.<]]>- Kervaire invariantWrite comment View comments
- <]]>
- KimWrite comment View comments
- <]]>
- KleimanWrite comment View comments
- <]]>
- KodairaWrite comment View comments
Collected works, 3 volumes
<]]>- Kolyvagin systemsWrite comment View comments
arXiv:0909.3916 Refined class number formulas and Kolyvagin systems from arXiv Front: math.NT by Barry Mazur, Karl Rubin We use the theory of Kolyvagin systems to prove (most of) a refined class number formula conjectured by Darmon. We show that for every odd prime $p$, each side of Darmon's conjectured formula (indexed by positive integers $n$) is "almost" a $p$-adic Kolyvagin system as $n$ varies. Using the fact that the space of Kolyvagin systems is free of rank one over $\mathbf{Z}_p$, we show that Darmon's formula for arbitrary $n$ follows from the case $n=1$, which in turn follows from classical formulas.
<]]>- KontsevichWrite comment View comments
I don't think he has a web page, but most of his papers seem to be on the arxiv. A preprint on periods is on the IHES preprint server.
<]]>- Koszul complexWrite comment View comments
For interpretation of Koszul complex as cofibrant replacement in cdgas (for algebras coing from a regular sequence), see Toen Essen talk, top of page 10.
arXiv:1004.0096 The Koszul complex is the cotangent complex from arXiv Front: math.KT by Joan Milles We extend the Koszul duality theory of associative algebras to algebras over an operad. Recall that in the classical case, this Koszul duality theory relies on an important chain complex: the Koszul complex. We show that the cotangent complex, involved in the cohomology theory of algebras over an operad, generalizes the Koszul complex.
<]]>- Koszul dualityWrite comment View comments
http://ncatlab.org/nlab/show/Koszul+duality
http://mathoverflow.net/questions/329/what-is-koszul-duality
http://mathoverflow.net/questions/39577/koszul-duality-and-algebras-over-operads
Koszul duality: Martinez-Villa and Solberg
arXiv:1001.2032 Koszul duality in algebraic topology - an historical perspective from arXiv Front: math.AT by Dev Sinha 2 people liked this We survey the topology which led to the original bar and cobar constructions, for both associative algebras and coalgebras and for Lie algebras and commutative coalgebras. These constructions are often viewed as part of the larger theory of Koszul duality of operads, so this survey is meant to offer an historical perspective on the most prominent cases of that theory. We also explain recent work which shows that Hopf/linking invariants for homotopy are at the heart of the duality between commutative algebras and Lie coalgebras.
arXiv:0912.1670 Derived Koszul Duality and Involutions in the Algebraic K-Theory of Spaces from arXiv Front: math.AT by Andrew J. Blumberg, Michael A. Mandell We interpret different constructions of the algebraic $K$-theory of spaces as an instance of derived Koszul (or bar) duality and also as an instance of Morita equivalence. We relate the interplay between these two descriptions to the homotopy involution. We define a geometric analog of the Swan theory $G^{\bZ}(\bZ[\pi])$ in terms of $\Sigma^{\infty}{+} \Omega X$ and show that it is the algebraic $K$-theory of the $E{\infty}$ ring spectrum $DX=S^{X_{+}}$.
<]]>- KrizWrite comment View comments
- <]]>
- KroneckerWrite comment View comments
Mathematische Werke, maybe 5 volumes
<]]>- KrullWrite comment View comments
Collected papers, 2 volumes
<]]>- Kudla conjecturesWrite comment View comments
arXiv:1205.6417 On Kudla's Green function for signature (2,2), part I from arXiv Front: math.NT by Rolf Berndt, Ulf Kuehn Around 2000 Kudla presented conjectures about deep relations between arithmetic intersection theory, Eisenstein series and their derivatives, and special values of Rankin L-series. The aim of this text is to work out the details of an old unpublished draft on the second authors attempt to prove these conjectures for the case of the product of two modular curves. The mayor difficulties in our situation are of analytical nature, therefore this text assembles some material concerning Kudla's Green function associated to this situation. We present a mild modification of this Green function that satisfies the requirements of being a Green function in the sense of Arakelov theory on the natural compactification in addition. Only this allows us to define arithmetic special cycles. We then prove that the generating series of those modified arithmetic special cycles is as predicted by Kudla's conjectures a modular form with values in the first arithmetic Chow group.
<]]>- Kunneth theoremWrite comment View comments
In for example Adams LNM0099 the Kunneth thm is derived as a special case of the UCT, for generalized cohomology theories. Can something similar be done in AG?
<]]>