Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- l-adic representationWrite comment View comments
Husemoller has a chapter on basic things related to elliptic curves
<]]>- l-adic sheavesWrite comment View comments
Gabber has a construction of the cat of l-adic sheaves, I think mentioned in a review of a Jannsen paper.
Ivorra is an expert on l-adic realization functors from various cats of mixed motives.
http://mathoverflow.net/questions/32478/a-nice-explanation-of-what-is-a-smooth-l-adic-sheaf
<]]>- L-functionWrite comment View comments
See L-function folder
Really cool: Database of L-functions, modular forms, and related objects
Many things by Deninger on arxiv, and maybe also in the Deninger folder.
Review of Faltings: The determinant of cohomology in the etale topology Theta functions can be viewed as the canonical section of the determinant of cohomology. The corresponding notion in the etale topology would be L-series. "All known constructions of p-adic L-functions seem to be related to some situation where some etale cohomology has vanishing Euler char.
Knapp, an introduction to the Langlands program. (Move to Langlands program?)
For results on Beilinson conjectures for L-functions of modular forms, see book by Scholl.
Tim Dokchitser on an algorithm for computing special values of motivic L-functions numerically.
Fontaine: Bourbaki seminar on special values (contains many references!)
Soulé: Bourbaki seminar on L-functions.
Grothendieck writes in a letter to Serre about L-functions of sheaves, of of complexes of sheaves, and relates global (Verdier?) duality to the functional equation, and perhaps also to Poincaré duality (or perhaps not).
Li Upper bounds on L-functions at the edge of the critical strip
Integral reps: Unified viewpoint of Sakellaridis http://arxiv.org/abs/0905.4245
Saito: Functional equations of L-functions of varieties over finite fields MR763423. Discusses the constants occurring in the functional eq and relates them to unramified class field theory of the variety. This paper does not seem to be available online, as of Sep 2009. Very obscure journal.
PCMI 2009 summer school program
Would like L-functions of mixed motives. Can we define L-functions for simplicial sheaves in a suitable sense???
arXiv:1009.0736 Quantum Statistical Mechanics, L-series and Anabelian Geometry from arXiv Front: math.NT by Gunther Cornelissen, Matilde Marcolli It is known that two number fields with the same Dedekind zeta function are not necessarily isomorphic. The zeta function of a number field can be interpreted as the partition function of an associated quantum statistical mechanical system, which is a C*-algebra with a one parameter group of automorphisms, built from Artin reciprocity. In the first part of this paper, we prove that isomorphism of number fields is the same as isomorphism of these associated systems. Considering the systems as noncommutative analogues of topological spaces, this result can be seen as another version of Grothendieck's "anabelian" program, much like the Neukirch-Uchida theorem characterizes isomorphism of number fields by topological isomorphism of their associated absolute Galois groups. In the second part of the paper, we use these systems to prove the following. If there is an isomorphism of character groups (viz., Pontrjagin duals) of the abelianized Galois groups of the two number fields that induces an equality of all corresponding L-series (not just the zeta function), then the number fields are isomorphic.This is also equivalent to the purely algebraic statement that there exists a topological group isomorphism as a above and a norm-preserving group isomorphism between the ideals of the fields that is compatible with the Artin maps via the other map.
http://mathoverflow.net/questions/72474/axioms-for-zeta-functions
http://mathoverflow.net/questions/75409/space-of-l-functions
<]]>- L-function IIWrite comment View comments
arXiv:1211.4459 Computing $L$-functions and semistable reduction of superelliptic curves fra arXiv Front: math.AG av Irene I. Bouw, Stefan Wewers We give an explicit description of the stable reduction of superelliptic curves of the form $y^n=f(x)$ at primes $\p$ whose residue characteristic is prime to the exponent $n$. We then use this description to compute the local $L$-factor of the curve and the exponent of conductor at $\p$.
arXiv:1211.4239 Cyclic homology, Serre's local factors and the $\lambda$-operations fra arXiv Front: math.AG av Alain Connes, Caterina Consani We show that for a smooth, projective variety X defined over a number field K, cyclic homology with coefficients in the ring of infinite adeles of K, provides the right theory to obtain, using the lambda-operations, Serre's archimedean local factors of the complex L-function of X as regularized determinants.
<]]>- L-infinity algebraWrite comment View comments
- <]]>
- Lambda-ringWrite comment View comments
Concrete nonsense blog post. See also Chern classes and RR formalism
http://www.ncatlab.org/nlab/show/special+lambda-ring
http://www.ncatlab.org/nlab/show/Lambda-ring
Discussion at the categories list in Dec 2009, see this conjecture.
<]]>- Landweber exactnessWrite comment View comments
- <]]>
- LangWrite comment View comments
Collected papers, 5 volumes
<]]>- Langlands programWrite comment View comments
Functional analysis on the eve of the 21st century Contains article by Kapranov on Langlands - must read! Follow-up here at MO.
See pubs and preprints of Frenkel, Ngo Bao Chau, and others
http://mathoverflow.net/questions/60368/langlands-conjectures-in-higher-dimensions
http://mathoverflow.net/questions/6457/kapranovs-analogies
http://mathoverflow.net/questions/58901/what-are-the-pillars-of-langlands
http://mathoverflow.net/questions/15370/tools-for-the-langlands-program
arXiv:1009.0785 The conjectural connections between automorphic representations and Galois representations from arXiv Front: math.NT by Kevin Buzzard, Toby Gee We state conjectures on the relationships between automorphic representations and Galois representations, and give evidence for them.
A conference on current developments.
I think there is a 2012 article by Parshin in Russian Mathematical Surveys which describes some kind of Langlands for higher local fields.
Motives volume 2, from page 363 and onwards.
Clozel on motives and automorphic forms: Among other things describing "algebraic" automorphic reps.
PAMQ page from Langlands instructional conference
http://mathoverflow.net/questions/1972/langlands-dual-groups
http://mathoverflow.net/questions/1252/where-stands-functoriality-in-2009
-
REFS FROM CAM STUDY GP:
http://pamq.henu.edu.cn/add/langp/245-302.pdf
Taylor's ICM article on Galois representations http://www.math.harvard.edu/~rtaylor/longicm02.dvi
Notes by Ito on Langlands correspondences
http://www.math.kyoto-u.ac.jp/~tetsushi/files/hakuba200611.pdf
Older article by Gelbart
http://www.ams.org/bull/1984-10-02/S0273-0979-1984-15237-6/S0273-0979-1984-15237-6.pdf
Not available online:
Bump "Automorphic forms and representations" (CUP) and Bernstein/Gelbart "An introduction to the Langlands Program" (Birkhaeuser).
For lots more references see http://pamq.henu.edu.cn/add/langp/notes/China2.dvi
For references on background like algebraic groups, modular forms, representation theory see http://pamq.henu.edu.cn/add/langp/notes/China1new.dvi
Old list of refs:
Bump
articles in Autom forms, shim var's and L-funcs, 1990
Gelbart/Shahidi; analytic properties of autom L-functions
Chapter 7 of ILP with its refs
Lectures on Automorphic L-functions/ cogdell, kim, murty Moreno: Advanced Analytic NT: L-functions
Henniart: Une preuve simple... (2000)
The volume on FLT
Arthur, Ellwood & Kottwitz: Harmonic analysis, the trace formula and Shimura varieties (publ. Date Jan 13, 2006)
Autom forms, representations adn L-functions. Proceedings of symposia in pure math. 2 volumes. Classmark QA331.S93. Electronic version on AMS homepage.
For p-adic langlands (Breuil), see stuff by Emerton
Autom forms, Shim varieties and L-functions. vol I, II. eds Clozel & Milne
<]]>- Langlands program globalWrite comment View comments
arXiv:0907.4527](http://front.math.ucdavis.edu/0907.4527) Lecture on Langlands Functoriality Conjecture from arXiv Front: math.AG by Jae-Hyun Yang This is a survey lecture note on the applications of Langlands functoriality which were obtained recently by some people at the Langalnds school. This lecture was delivered at the Department of Mathematics, Kyoto University, Japan on June 30 (Tuesday), 2009.
See Lafforgues webpage for several papers on his recent ideas.
http://mathoverflow.net/questions/1252/where-stands-functoriality-in-2009
http://mathoverflow.net/questions/104397/base-change-and-automorphic-induction-for-gl-1
http://mathoverflow.net/questions/31538/non-abelian-class-field-theory-and-fundamental-groups
http://mathoverflow.net/questions/1972/langlands-dual-groups
http://mathoverflow.net/questions/74472/what-makes-langlands-for-n2-easier-than-langlands-for-n2
http://mathoverflow.net/questions/33269/fontaine-mazur-for-gl-1
http://mathoverflow.net/questions/75335/what-is-the-reason-for-modularity-results
arXiv:1003.4578 Formule des Traces et Fonctorialité: le Début d'un Programme from arXiv Front: math.AG by Edward Frenkel, Robert Langlands, Ngo Bao Chau We outline an approach to proving functoriality of automorphic representations using trace formula. More specifically, we construct a family of integral operators on the space of automorphic forms whose eigenvalues are expressed in terms of the L-functions of automorphic representations and begin the analysis of their traces using the orbital side of the stable trace formula. We show that the most interesting part, corresponding to regular conjugacy classes, is nothing but a sum over a finite-dimensional vector space over the global field, which we call the Steinberg-Hitchin base. Therefore it may be analyzed using the Poisson summation formula. Our main result is that the leading term of the dual sum (the value at 0) is precisely the dominant term of the trace formula (the contribution of the trivial representation). This gives us hope that the full Poisson summation formula would reveal the patterns predicted by functoriality.
Buzzard email: Let me finish by explaining what will be happening in the Langlands study group. Langlands made some conjectures, perhaps slightly vague at first but gradually becoming more precise in the 80s, relating the L-functions of Shimura varieties to the L-functions attached to automorphic forms. These conjectures vastly generalise the work of Eichler-Shimura/Ihara which shows that the L-function of a modular curve can be expressed in terms of the L-functions attached to modular forms. Definitive steps towards their proof were made in the 80s (Langlands, Rapoport; Langlands gave a completely new proof of Eichler-Shimura/Ihara) and 90s (Kottwitz, Reimann, Milne). My initial plan was to go through Kottwitz' paper but I am still at the stage where I break out in a sweat whenever I open it. My current plan is to start off slowly, with Langlands' proof of the modular curve case (which is vastly different to Eichler-Shimura's proof but more amenable to generalisation), and then to move on to principally polarized abelian varieties, where Eichler-Shimura breaks down to a large extent but Langlands' methods do not. We'll see how far we get.
<]]>- Langlands program localWrite comment View comments
arXiv:1001.3226 Good reduction of affinoids on the Lubin-Tate tower from arXiv Front: math.AG by Jared Weinstein We analyze the geometry of the tower of Lubin-Tate deformation spaces, which parametrize deformations of a one-dimensional formal module of height h together with level structure. According to the conjecture of Deligne-Carayol, these spaces realize the local Langlands correspondence in their l-adic cohomology. This conjecture is now a theorem, but currently there is no purely local proof. Working in the equal characteristic case, we find a family of affinoids in the Lubin-Tate tower with good reduction equal to a rather curious nonsingular hypersurface, whose equation we present explicitly. Granting a conjecture on the L-functions of this hypersurface, we find a link between the conjecture of Deligne-Carayol and the theory of Bushnell-Kutzko types, at least for certain class of wildly ramified supercuspidal representations of small conductor.
<]]>- LaTeXWrite comment View comments
UltraTex emacs mode
For BibTeX data: K-theory file, Google scholar, and/or MathSciNet.
Useful: dvips -p 12 -l 24 myfile; ps2pdf myfile.ps
About hyperlinks: http://en.wikibooks.org/wiki/LaTeX/Hyperlinks
GmailTex is a Chrome extension for tex rendering in Gmail.
<]]>- Lawvere theoryWrite comment View comments
http://nlab.mathforge.org/nlab/show/Lawvere+theory
http://ncatlab.org/nlab/show/Lawvere%27s+reconstruction+theorem
See Cranch thesis for algebraic theories in infinity-cats.
<]]>- Lax functorWrite comment View comments
http://ncatlab.org/nlab/show/lax+functor
http://nlab.mathforge.org/nlab/show/lax+natural+transformation
<]]>- Lefschetz fixed point formulaWrite comment View comments
arXiv:1002.2142 A Lefschetz fixed point formula for singular arithmetic schemes with smooth generic fibres from arXiv Front: math.AG by Shun Tang In this article, we consider singular equivariant arithmetic schemes whose generic fibres are smooth. For such schemes, we prove a relative fixed point formula of Lefschetz type in the context of Arakelov geometry. This formula is an analog, in the arithmetic case, of the Lefschetz formula proved by R. W. Thomason. In particular, our result implies a fixed point formula which was conjectured by V. Maillot and D. Rössler.
<]]>- Lefschetz hyperplane theoremWrite comment View comments
- <]]>
- Lefschetz standard conjectureWrite comment View comments
One of the two Grothendieck standard conjectures. See Kleiman in Motives.
<]]>- Lefschetz trace formulaWrite comment View comments
[arXiv:1008.3689] L-series of Artin stacks over finite fields from arXiv Front: math.NT by Shenghao Sun We reprove the Lefschetz trace formula for stacks (in the context of derived categories and the six operations for stacks developed by Laszlo and Olsson), and give the meromorphic continuation of L-series (in particular, zeta functions) of Artin stacks over a finite field. We also give an upper bound for the weights of the cohomology groups of stacks, and an "independence of l" result for a certain class of quotient stacks.
<]]>- Left homotopyWrite comment View comments
Let
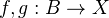 be morphisms in a model category. A left homotopy from
be morphisms in a model category. A left homotopy from  to
to 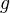 is a map
is a map 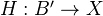 for some cylinder object
for some cylinder object 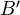 for
for 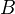 such that
such that 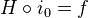 and
and 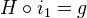 . Here
. Here 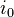 and
and 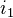 are the obvious maps. Say
are the obvious maps. Say  and
and 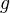 are left homotopic if there exists such a thing.<]]>
are left homotopic if there exists such a thing.<]]>- Leopoldt conjectureWrite comment View comments
Mihailescu http://arxiv.org/abs/0905.1274. Maybe also other articles, search if necessary.
http://londonnumbertheory.wordpress.com/2009/11/08/leopoldts-conjecture/
<]]>- LerayWrite comment View comments
Works, 3 volumes
<]]>- LevineWrite comment View comments
- <]]>
- LichtenbaumWrite comment View comments
- <]]>
- Lichtenbaum-Quillen conjecturesWrite comment View comments
A good reference is probably Kahn in Handbook of K-theory.
Here is an exposition of Thomason's work.
The Q-L conjecture at the prime 2, by Kahn.
arXiv:1211.1651 Unstable analogues of the Lichtenbaum-Quillen conjecture fra arXiv Front: math.KT av Marian Anton, Joshua Roberts This survey is mostly concerned with unstable analogues of the Lichtenbaum-Quillen Conjecture. The Lichtenbaum-Quillen Conjecture (now implied by the Voevodsky-Rost Theorem) attempts to describe the algebraic K-theory of rings of integers in number fields in terms of much more accessible "etale models". Suitable versions of the conjecture predict the cohomology of infinite general linear groups of rings of S-integers over suitable number fields; our survey focuses on an unstable version of this form of the conjecture.
<]]>- Lie algebraWrite comment View comments
nlab definition in terms of operads
http://www.ncatlab.org/nlab/show/universal+enveloping+algebra
<]]>- Lie groups and Lie algebrasWrite comment View comments
See Rep and Lie theory folder
Notes by Amy from Grojnowski's course
LNM0040 Tits: Tables of Lie groups and their reps
http://www.ncatlab.org/nlab/show/Lie+theory
Many Bourbaki seminars, here are some selected ones:
- Exp 57: Algebraic Lie groups (works of Chevalley)
- Exp 96: Apres Harish-Chandra
- Exp 100: Serre on the work of Borel and Weil
<]]>- Lifting varietiesWrite comment View comments
- <]]>
- Limits and colimtsWrite comment View comments
- <]]>
- List of spectral sequencesWrite comment View comments
Eventually, search the database for spectral sequence.
Weight spectral sequence
Descent spectral sequence
Spectral sequences from the six functors formalism
Curtis spectral sequence (mentioned in Toen)
Adams spectral sequence
Grothendieck's spectral sequence
Leray spectral sequence
Hypercohomology spectral sequence (two, I think)
Motivic spectral sequence
Atiyah-Hirzebruch spectral sequence
Homotopy spectral sequence for a cosimplicial space. Obtained by Bousfield and Kan as a consequence of a model structure on cosimplicial simplicial sets.
Bousfield-Kan spectral sequence: "The prototype of all second-quadrant homotopy spectral sequences".
Descent spectral sequence. (In Jardine: Gen etale cohomology, p 251, this spectral sequence is for the homotopy groups of a spectrum (or perhaps sheaf of spectra?????). A principle: Bounds on cohomological dimension (in terms of Krull dimension?) force descent spectal sequences to converge.
<]]>- Local LanglandsWrite comment View comments
Notes on the project suggested by Matthias Strauch.
See Strauch list of references
http://arxiv.org/PS_cache/math/pdf/0204/0204053v2.pdf
The article by Morava
Should also check with Lurie perhaps.
Some useful things are explained in this article by Rezk
Read slides of Strickland for background.
<]]>- Local systemWrite comment View comments
LNM0163 Deligne lectures on local systems, integrable connections, Gauss-Manin conn, differential eqs, regularity at infinity, etc.
<]]>- LocaleWrite comment View comments
Could ask Julia for refs maybe (her essay???)
<]]>- LocalizationWrite comment View comments
Would like to clarify all different notions of localization, for example the relation between localization in number theory and in homotopy theory.
Gabriel-Zisman in Htpy th folder: Simplicial sets, Localization (in the sense of inverting some morphisms)
Dwyer-Spalinski in the homotopy theory folder: Model categories, Homotopy limits brief intro, localization wrt a homology theory: very brief intro on p. 54.
http://ncatlab.org/nlab/show/category+of+fractions
http://ncatlab.org/nlab/show/local+object
http://ncatlab.org/nlab/show/localization+of+an+(infinity,1)-category
http://ncatlab.org/nlab/show/localization+of+a+simplicial+model+category
http://ncatlab.org/nlab/show/Ore+localization
http://nlab.mathforge.org/nlab/show/Bousfield+localization
http://ncatlab.org/nlab/show/simplicial+localization
http://www.ncatlab.org/nlab/show/homotopy+localization
The localization of any category wrt any class of morphisms is briefly described in Toen: Essen talk. Also ref to Dwyer-Kan hammock localization. See also remark 2.4.4 and preceeding pragraphs for a coneptual discussion of different notions of localization. Section 2.6 treats homotopical localization, and left Bousfield loc.
See also Bousfield localization
For localization in the context of DG-categories, and also a discussion of Gabriel-Zisman, see Toen: Lecture on DG-categories. File Toen web unpubl swisk.pdf.
Dwyer (2006): Noncommutative localisation in homotopy theory
Ravenel: Localization and periodicity in homotopy theory (1987)
Something by Kahn and Sujatha
Perhaps the book by Dwyer-Hirschhorn-Kan treats localisation in a good way?
Section 12 in Baues: Homotopy types. For a generalized homology theory
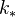 , there is a somewhat unclear def of
, there is a somewhat unclear def of 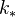 -equivalence,
-equivalence, 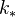 -local space, and a map being a
-local space, and a map being a 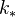 -localization. Equiv of cats between the localization of
-localization. Equiv of cats between the localization of  wrt
wrt 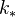 -eqiuvalences, and the homotopy cat of
-eqiuvalences, and the homotopy cat of 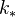 -local spaces, sending a CW space to its
-local spaces, sending a CW space to its 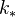 -localization. Can view
-localization. Can view 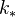 -equivalences as WEs in a "cofibration cat". More related to localization, omitted here, e.g. Postnikov stuff.
-equivalences as WEs in a "cofibration cat". More related to localization, omitted here, e.g. Postnikov stuff.Localisation of CW complexes
Let
 be an arbitrary set of primes. We say that an abelian group is
be an arbitrary set of primes. We say that an abelian group is  -local if multiplication by
-local if multiplication by  is an isomorphism for all
is an isomorphism for all 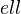 NOT in
NOT in  . A homomorphism is a
. A homomorphism is a  -localisation if the target is
-localisation if the target is  -local and satisfies the obvious universal property.
-local and satisfies the obvious universal property.Consider the category
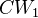 of 1-connected CW complexes. An
of 1-connected CW complexes. An  in this category is called
in this category is called  -local if
-local if 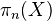 is
is  -local for all
-local for all  . A morphism is a
. A morphism is a  -localisation if the target is
-localisation if the target is  -local and is universal with respect to this property. (The universal property here refers to a bijection of homotopy classes of maps, so we are really in the homotopy category.)
-local and is universal with respect to this property. (The universal property here refers to a bijection of homotopy classes of maps, so we are really in the homotopy category.) Fact: Any
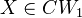 has a
has a  -localisation, unique up to homotopy.
-localisation, unique up to homotopy.  -localisation is a functor (I think).
-localisation is a functor (I think).Thm: TFAE, for a morphism
 in
in 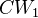 :
:  is a
is a  -localisation
-localisation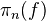 is a
is a  -localisation for all
-localisation for all 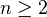
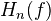 is a
is a  -localisation for all
-localisation for all 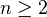
Example: Let
 consist of a single prime
consist of a single prime 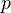 . Then homotopy and homology groups (and maps between them) are obtained by tensoring with
. Then homotopy and homology groups (and maps between them) are obtained by tensoring with 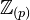 .
.Example: Let
 consist of all primes except
consist of all primes except 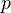 . Then homotopy and homology groups (and maps between them) are obtained by tensoring with
. Then homotopy and homology groups (and maps between them) are obtained by tensoring with 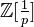
In Kono-Tamaki, there are also further compatibilities, and a construction of the
 -localisation.
-localisation.A Generalized cohomology theory
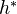 , and a set
, and a set  of primes, define a generalized cohomology theory
of primes, define a generalized cohomology theory 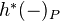 , because
, because  -localisation is exact on
-localisation is exact on 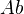 . If the coefficient group of
. If the coefficient group of 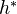 is
is  -local, then the natural transformation from
-local, then the natural transformation from 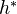 to its
to its  -localisation is an isomorphism.
-localisation is an isomorphism.Theorem: Isomorphism on
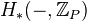 implies isomorphism on
implies isomorphism on 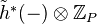 <]]>
<]]>- Localization 2Write comment View comments
Jardine-Goerss intro to chapter IX
Localization is more a way of life than any one specific result. For example, under this rubric one can include Bousfield localization with respect to a ho- mology theory, localization with respect to a map as pioneered by Bousfield, Dror-Farjoun and elaborated on by many others, and even the formation of the stable homotopy category. We will touch on all three of these subjects, but we also have another purpose. There is a body of extremely useful techniques that we will explore and expand on. These have come to be known as Bousfield factor- ization, which is a kind of “trivial cofibration-fibration” factorization necessary for producing localizations, and the Bousfield-Smith cardinality argument. This latter technique arises when one is confronted with a situation where a fibration is defined to be a map which has the right lifting property with respect to some class of maps. However, for certain arguments one needs to know it is sufficient to check that the map has the right lifting property with respect to a set of maps. We explain both Bousfield factorization and the cardinality argument and explore the implications in a variety of contexts. In particular, we explore localization in diagram categories, with an eye towards producing a model for the stable homotopy category, and we produce a simplicial model category structure on categories of diagrams that will be useful in a later discussion of homotopy inverse limits.
The concept of localization probably has its roots in the notion of a Serre class of abelian groups and the Whitehead Theorem mod a Serre class [86, §9.6]. This result is still useful and prevalent — so prevalent, in fact, that it is often used without reference. The idea of localizing a space with respect to a homology theory appeared in Sullivan’s work on the Adams conjecture [85], where there is an explicit localization of a simply connected space with respect to ordinary homology with Z[1/p] coefficients. Bousfield and Kan [14] gave the first cate- gorical definition of localization with respect to homology theory and provided a localization for nilpotent spaces with respect to H∗(·, R), where R = Fp for some prime p or R a subring of the rationals. Their technique was the R-completion of space, recapitulated in Section 3 below for the case R = Fp. It was Bousfield himself who introduced model category theoretic techniques to provide the lo- calization of any space with respect to an arbitrary homology theory. His paper [8] has been enormously influential, as much for the methods as for the results, and it’s hard to overestimate its impact. For example, the concept of localization with respect to a map and the construction of its existence, which appears in the work for Dror-Farjoun [22] and [23] is directly influenced by Bousfield’s ideas. About the time Dror-Farjoun’s papers were first circulating, a whole group of people began to explore these ideas, both in homotopy theory and in relatedalgebraic subjects. The paper by Cascuberta [17] is a useful survey. One should also mention the important paper of Bousfield [11], which uses similar techniques for its basic constructions. The longest and most general work in this vein, a work that includes an exposition of the localization model category in an arbi- trary cellular model category is that of Hirschhorn [42], available at this writing over the Internet. The notion of a cellular model category is one way of axioma- tizing the structure necessary to make Bousfield’s arguments work, based on the concept of cell complexes and inclusions of sub-complexes. We give, in Section 4, a slightly different list of hypotheses along these lines. Both systems of axioms work in any example that we know. We emphasize, however, that Bousfield’s ideas had influence outside of the area of homotopy localization. For example, Jeff Smith realized very early on that one could use these constructions to put a model category structure on the category of small diagrams of simplicial sets, so that homotopy inverse limits can be computed as total right derived functors of inverse limit. This never made it into print, and we go through the arguments in Section 5. Beyond this, there is the second author’s work on the homotopy theory of simplicial presheaves [46], see also [38] as well as Joyal’s result for simplicial sheaves [53]. In the context of the present discussion that work can be interpreted as follows: the category of presheaves on a Groethendieck site is a category of diagrams and there is a closed model category structure obtained by localizing with respect to a class of cofibrations determined by the topology of the underlying site. END
<]]>- Localization 3Write comment View comments
http://mathoverflow.net/questions/2931/localizations-of-categories
http://nlab.mathforge.org/nlab/show/localization
http://www.ncatlab.org/nlab/show/simplicial+localization
Sullivan's MIT notes (Homotopy folder). Excellent stuff on localizations, completions, profinite, p-local and rational homotopy types. p-adic homotopy theory. Relation to etale homotopy theory! Remark: The Sullivan conjecture is about the contractibility of the space of maps from the classifying space of a finite group to a finite-dimensional CW complex.
<]]>- Locally compact groupsWrite comment View comments
For Haar measure and other results, see Valenza and Ramakrishnan: Fourier analysis on Number Fields
Serre: Bourbaki exp 27. Nice results of Iwasawa and Gleason
Borel: Bourbaki exp 29.
LNM0002 treats cohomology of locally compact spaces. The treatment looks "elementary" and pre-Grothendieck.
<]]>- Log geometryWrite comment View comments
See folder AG/Log geometry
Book by Ogus online???
http://mathoverflow.net/questions/12569/references-for-logarithmic-geometry
<]]>- Log minimal programWrite comment View comments
arXiv:0907.1506 Introduction to the log minimal model program for log canonical pairs from arXiv Front: math.AG by Osamu Fujino We describe the foundation of the log minimal model program for log canonical pairs according to Ambro's idea. We generalize Kollár's vanishing and torsion-free theorems for embedded simple normal crossing pairs. Then we prove the cone and contraction theorems for quasi-log varieties, especially, for log canonical pairs.
arXiv:1103.2140 Logarithmic stacks and minimality from arXiv Front: math.AG by W. D. Gillam Given a category fibered in groupoids over schemes with a log structure, one produces a category fibered in groupoids over log schemes. We classify the groupoid fibrations over log schemes that arise in this manner in terms of a categorical notion of "minimal" objects. The classification is actually a purely category-theoretic result about groupoid fibrations over fibered categories, though most of the known applications occur in the setting of log geometry, where our categorical framework encompasses many notions of "minimality" previously extant in the literature.
<]]>- Logarithmic structuresWrite comment View comments
Rognes preprints in progress (as of Sep 2009), including: Complex oriented logarithmic structures, Logarithmic topological cyclic homology
Logarithmic structures of Fontaine-Illusie.
See also various log cohomology theories
[arXiv:0909.0288] Geography of log models:theory and applications from arXiv Front: math.AG by Sung Rak Choi, Vyacheslav Shokurov An introduction to geography of log models with applications to positive cones of FT varieties and to geometry of minimal models and Mori fibrations.
arXiv:1006.5870 Logarithmic Geometry and Moduli from arXiv Front: math.AG by Dan Abramovich, Qile Chen, Danny Gillam, Yuhao Huang, Martin Olsson, Matthew Satriano, Shenghao Sun We discuss the role played by logarithmic structures in the theory of moduli.
http://mathoverflow.net/questions/70186/more-questions-about-log-structures
arXiv:1001.0466 Parabolic sheaves on logarithmic schemes fra arXiv Front: math.NT av Niels Borne, Angelo Vistoli We show how the natural context for the definition of parabolic sheaves on a scheme is that of logarithmic geometry. The key point is a reformulation of the concept of logarithmic structure in the language of symmetric monoidal categories, which might be of independent interest. Our main result states that parabolic sheaves can be interpreted as quasi-coherent sheaves on certain stacks of roots.
Oslo 2009 The aim of the conference is to develop the current interplay between arithmetic algebraic geometry and stable homotopy theory. Using structured ring spectra one can form topological structure sheaves for moduli stacks of elliptic curves or other abelian varieties, whose ring spectra of global sections define powerful new homology theories. Using sheaves of infinity-categories one can form topological crystalline cohomology, with associated de Rham-Witt complexes closely related to topological cyclic homology and p-adic algebraic K-theory. For complete local rings of mixed characteristic, or for structured ring spectra of mixed chromatic types, there are log (= logarithmic) geometric extensions of these theories, leading to de Rham-Witt complexes with log poles, log topological cyclic homology and log K-theory. The hope is that both algebraic geometers and homotopy theorists will have something to learn from the modern developments in these adjacent fields.
<]]>- Long exact sequenceWrite comment View comments
I think Voevodsky writes somewhere (ICM talk??) that all long exact sequences arise from a cohomological functor applied to some distinguished triangle in a triangulated category.
<]]>- Loop spaceWrite comment View comments
See orange book by Adams.
A great introduction seems to be Chapter 13 of Handbook of AT, in Alg Top folder
http://ncatlab.org/nlab/show/loop+space
http://ncatlab.org/nlab/show/loop+space+object
http://ncatlab.org/nlab/show/connective+spectrum
http://ncatlab.org/nlab/show/infinite+loop+space
http://mathoverflow.net/questions/65103/uniqeness-of-loop-spaces
Jardine-Goerss chapter V.5 and V.6 describes the loop space of a simplicial group as left adjoint to a certain construction of a model for the classifying space.
Understand the infinite loop space machines of Thomason and May
Some good stuff might be in May's books
Rings, modules, and algebras in infinite loop space theory, by Anthony D. Elmendorf and Michael A. Mandell K0748
Something on approximation by smooth manifolds: K0592
arXiv:1002.3636 Loop Spaces and Connections from arXiv Front: math.AT by David Ben-Zvi, David Nadler We examine the geometry of loop spaces in derived algebraic geometry and extend in several directions the well known connection between rotation of loops and the de Rham differential. Our main result, a categorification of the geometric description of cyclic homology, relates S^1-equivariant quasicoherent sheaves on the loop space of a smooth scheme or geometric stack X in characteristic zero with sheaves on X with flat connection, or equivalently DX-modules. By deducing the Hodge filtration on de Rham modules from the formality of cochains on the circle, we are able to recover DX-modules precisely rather than a periodic version. More generally, we consider the rotated Hopf fibration Omega S^3 --> Omega S^2 --> S^1, and relate Omega S^2-equivariant sheaves on the loop space with sheaves on X with arbitrary connection, with curvature given by their Omega S^3-equivariance.
May LNM0099 gives and exposition which seems old/early but maybe therefore easier to grasp.
LNM0161 Stasheff on H-spaces and loop spaces
LNM0196 contains historical survey on infinite loop spaces by Stasheff, really nice
Goerss-Jardine mentions that the loop space of a simplicial set should be the loops of a fibrant model, in other words the loop functor is a total right derived functor.
arXiv:1009.0804 The homotopy theory of function spaces: a survey from arXiv Front: math.AT by Samuel Bruce Smith We survey research on the homotopy theory of the space map(X, Y) consisting of all continuous functions between two topological spaces. We summarize progress on various classification problems for the homotopy types represented by the path-components of map(X, Y). We also discuss work on the homotopy theory of the monoid of self-equivalences aut(X) and of the free loop space LX. We consider these topics in both ordinary homotopy theory as well as after localization. In the latter case, we discuss algebraic models for the localization of function spaces and their applications.
<]]>- Lubin-Tate theoryWrite comment View comments
arXiv:0910.1132 Explicit non-abelian Lubin-Tate theory for GL(2) from arXiv Front: math.AG by Jared Weinstein Let $F$ be a non-Archimedean local field with residue field $k$ of odd characteristic, and let $B/F$ be the division algebra of rank 4. We explicitly construct a stable curve $\mathfrak{X}$ over the algebraic closure of $k$ admitting an action of $GL2(F)\times B^\times \times WF$ which realizes the Jacquet-Langlands correspondence and the local Langlands correspondence in its cohomology.
arXiv:0911.5238 Continuous homotopy fixed points for Lubin-Tate spectra from arXiv Front: math.AT by Gereon Quick We construct a stable model structure on profinite symmetric spectra with a continuous action of an arbitrary profinite group. This provides a natural framework for a new construction of homotopy fixed point spectra and of homotopy fixed point spectral sequences for the action of the extended Morava stabilizer group on Lubin-Tate spectra. These continuous homotopy fixed points are canonically equivalent to the homotopy fixed points of Devinatz and Hopkins but have a drastically simplified construction.
<]]>- LurieWrite comment View comments
- <]]>
- Lusternik-Schnirelmann stuffWrite comment View comments
Bourbaki exp 36
<]]>