Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- Mac LaneWrite comment View comments
See Selected Papers
<]]>- MahantaWrite comment View comments
- <]]>
- MaltsiniotisWrite comment View comments
- <]]>
- ManifoldWrite comment View comments
For the various types of manifolds, see Dieudonne: Panorama. The definition of manifold includes the existence of charts and transition functions. The definition of PL manifold, differentiable mfd, real analytic and complex analytic mfd involves conditions on the transition functions.
Given a (differentiable???) mfd M, have a notion of G-structure on M. Specific choices of G leads to the notions of Riemannian structure (orthogonal gp), pseudo-Riemannian str (Lorentz group), symplectic str (symplectic grp), and almost complex str (complex general linear group). Any complex analytic mfd comes with an almost complex str, but the converse is true only if the almost complex str is "integrable" (I think).
http://www.ncatlab.org/nlab/show/G-structure
http://nlab.mathforge.org/nlab/show/manifold
There are various things by Thurston available on giga.
http://mathoverflow.net/questions/116814/torsion-in-cohomology-of-smooth-manifolds
Manifolds: Many references in the Manifolds folder.
<]]>- ManinWrite comment View comments
Check Algebra, Arithmetic and Geometry (in honor of Manin), 2008.
Selected papers, see scan
<]]>- Manin conjectureWrite comment View comments
arXiv:1009.2364 Manin's Conjecture for a Singular Sextic del Pezzo Surface from arXiv Front: math.NT by Daniel Loughran We prove Manin's conjecture for a del Pezzo surface of degree six which has one singularity of type $\mathbf{A}_2$. Moreover, we achieve a meromorphic continuation and explicit expression of the associated height zeta function.
<]]>- MarcolliWrite comment View comments
- <]]>
- MathematiciansWrite comment View comments
Some of my favourite mathematicians. "S" means that I have downloaded their interesting articles and listed the missing ones in scratchbook. "I" means that I have indexed his/her work in the DB, i.e. skimmed and taken brief notes.
- Adams
- André S
- Anel S
- Arakelov S
- Arapura S
- Arthur S
- Artin S
- Arndt
- Atiyah S
- Ayoub S
- Barbieri Viale S
- Baues S
- Beilinson S
- Berglund
- Biglari S
- Bloch S
- Bondarko S
- Bost
- Bourbaki
- Brauer S
- Breen S
- Bridgeland S
- Burgos Gil S
- Borel S
- Borger S
- Bott
- Brown S
- Bondal S
- Bousfield S
- Cartan S
- Cartier S
- Chern S
- Chow S
- Connes S maybe not complete
- Conrad
- Consani S
- Cortinas S
- Cox S
- Cisinski S
- Crane S
- Curtis S
- de Jeu S
- de Jong S
- Dedekind
- Deninger S
- Déglise S
- Deligne S
- Demazure S
- Dokchitser S
- Drinfeld
- Dugger S
- Dwyer S
- Ehresmann
- Eilenberg
- Ekedahl
- Emerton
- Eriksson
- Esnault
- Faltings S
- Feliu S
- Friedlander S
- Fontaine
- Gabber S
- Gelbart
- Gelfand
- Gersten S
- Geisser S
- Gepner
- Gille S
- Gillet S
- Giraud S
- Goerss S
- Griffiths
- Godement S
- Goncharov S
- Grayson S
- Gromov
- Gross
- Grothendieck S
- Guillen S
- Guletskii S
- Hain S
- Hanamura S
- Harada S
- Harish-Chandra
- Hecke
- Heller S
- Hironaka
- Hirzebruch
- Hodge
- Hollander S
- Hoobler S
- Hopf
- Hovey S
- Hopkins S
- Hornbostel S
- Hurewicz
- Hu S
- Huber (Annette) S
- Huybrechts S
- Illusie S
- Isaksen S
- Ivorra
- Iwasawa
- Jannsen S
- Jardine S
- Joshua S
- Jouanolou S
- Joyal S
- Kan S
- Katz
- Katzarkov
- Kedlaya S
- Kim (Minhyong) S
- Kahn S
- Kapranov S
- Kashiwara
- Keller S
- Kato S
- Kleiman S
- Kodaira
- Kontsevich S
- Kostant
- Koszul
- Kronecker
- Krull
- Kriz S
- Lafforgue
- Lang
- Langlands S
- Lawson S
- Laumon
- Lazarev
- Leray
- Levine S
- Lichtenbaum S
- Lipman
- Loday
- Lurie S
- Mac Lane
- Mahanta
- Maillot S
- Mandell S
- Manin (have not checked all MathSciNet, but see Selected papers in Manin folder)
- Murre S
- Mitchell S
- Miller
- Milne S
- Marcolli S
- Mazur S
- Messing
- Milnor
- Morel S
- May S
- Maltsiniotis S
- Morava S
- Morse
- Mumford
- Nagata
- Narasimhan
- Naumann S
- Navarro Aznar S
- Neeman S
- Nekovar S
- Nisnevich
- Niziol S
- Noether
- Nori
- Novikov
- Olsson S
- Orlov S
- Ostvaer S
- O´Sullivan
- Pandharipande
- Panin S
- Pantev
- Park S
- Parshin S
- Picard
- Pirashvili S
- Poincaré
- Pontryagin
- Pridham S
- Puppe
- Quillen S
- Rezk S
- Riemann
- Riou S
- Rydh S
- Roendigs S
- Rognes S
- Rosenschon
- Rossler S
- Rost S incomplete
- Saito S (S for all three)
- Samuel
- Sarnak
- Schechtman
- Schwede S
- Schmidt S
- Scholl S
- Segal
- Sergeraert
- Severi
- Severitt
- Serre see Oeuvres
- Selberg
- Shimura see Collected papers (Springer)
- Shipley S
- Simpson
- Shafarevich
- Snaith S
- Soulé S
- Spitzweck S
- Steenrod
- Stein
- Street
- Strickland S
- Suslin S
- Tabuada S
- Takeda S
- Tate S
- Totaro S
- Thomason S
- Toen S
- Tsalidis S
- Varadarajan
- Vezzosi S
- Voevodsky S
- Verdier
- Weibel S
- Waldhausen S
- Weil see Oeuvres
- Weyl
- Whitehead
- Wildeshaus S
- Witt
- Yagunov
- Yoshida
- Zariski
Add the following: Bourbaki people, and automorphic people: Frenkel, Gelbart, Arthur, Shahidi, Piatetiskii-Shapiro, Rapoport, Zink, Yekutieli, Wells.
See the Fields medallists volume for Atiyah, Novikov, Mumford, Voevoedsky, Mori, Connes, Witten, Kontsevich.
<]]>- MathJaxWrite comment View comments
- <]]>
- Maurer-Cartan equationWrite comment View comments
- <]]>
- MayWrite comment View comments
Papers of May
Web page of May
Some publications:
- Parametrized homotopy theory, by J. P. May and J. Sigurdsson
- The geometry of iterated loop spaces.
- Equivariant homotopy and cohomology theory.
<]]>- Mayer-VietorisWrite comment View comments
http://mathoverflow.net/questions/23175/mathematically-mature-way-to-think-about-mayervietoris
http://mathoverflow.net/questions/97621/mayer-vietoris-implies-excision
<]]>- MazurWrite comment View comments
- <]]>
- MessingWrite comment View comments
- <]]>
- Meta-mathematicsWrite comment View comments
- <]]>
- Metric geometryWrite comment View comments
Metric geometry: See Metric stuff folder. Among other things, book by Gromov on Metric structures
<]]>- MilneWrite comment View comments
- <]]>
- MilnorWrite comment View comments
Collected papers, at least 3 vols
<]]>- Milnor ConjectureWrite comment View comments
One of the main outcomes of Voevodsky's work on motivic cohomology. Here is his original paper, and here are some notes by Kahn. Here are Voevodsky's Seattle Lectures. This might be an updated version of the original article.
Another paper by Orlov, Vishik and Voevodsky
<]]>- Mirror symmetryWrite comment View comments
Many things in folder AG/Mirror symmetry
HMS for toric varieties: Abouzaid
http://mathoverflow.net/questions/40062/roadmap-for-mirror-symmetry
Meet HMS: http://arxiv.org/abs/0801.2014
HMS: See all by Seidel, books and arXiv
Names: Katzarkov, Sheridan, Orlov, Kontsevich. Orlov has a couple of surveys on arxiv.
MR2336692 (2008h:53151) Neeman, Amnon An infinite version of homological mirror symmetry. Real and complex singularities, 290--298, World Sci. Publ., Hackensack, NJ, 2007
Seidel book: Fukaya categories and Picard-Lefschetz theory
http://mathoverflow.net/questions/2905/is-the-fukaya-category-defined
arXiv:0908.1256 String modular motives of mirrors of rigid Calabi-Yau varieties from arXiv Front: math.AG by Savan Kharel, Monika Lynker, Rolf Schimmrigk The modular properties of some higher dimensional varieties of special Fano type are analyzed by computing the L-function of their $\Omega-$motives. It is shown that the emerging modular forms are string theoretic in origin, derived from the characters of the underlying rational conformal field theory. The definition of the class of Fano varieties of special type is motivated by the goal to find candidates for a geometric realization of the mirrors of rigid Calabi-Yau varieties. We consider explicitly the cubic sevenfold and the quartic fivefold, and show that their motivic L-functions agree with the L-functions of their rigid mirror Calabi-Yau varieties. We also show that the cubic fourfold is string theoretic, with a modular form that is determined by that of an exactly solvable K3 surface.
[arXiv:0907.3903] Homological mirror symmetry for curves of higher genus from arXiv Front: math.AG by Alexander I. Efimov Katzarkov has proposed a generalization of Kontsevich's mirror symmetry conjecture, covering some varieties of general type. Seidel \cite{Se} has proved a version of this conjecture in the simplest case of the genus two curve. Basing on the paper of Seidel, we prove the conjecture (in the same version) for curves of genus $g\geq 3,$ relating the Fukaya category of a genus $g$ curve to the category of Landau-Ginzburg branes on a certain singular surface. We also prove a kind of reconstruction theorem for hypersurface singularities. Namely, formal type of hypersurface singularity (i.e. a formal power series up to a formal change of variables) can be reconstructed, with some technical assumptions, from its D$(\Z/2)$-G category of Landau-Ginzburg branes. The precise statement is Theorem 1.2.
[arXiv:0910.2014] Homological mirror symmetry of Fermat polynomials from arXiv Front: math.AG by So Okada We discuss homological mirror symmetry of Fermat polynomials in terms of derived Morita equivalence between derived categories of coherent sheaves and Fukaya-Seidel categories (a.k.a. perfect derived categories of directed Fukaya categories), and some related aspects such as stability conditions, (kinds of) modular forms, and Hochschild homologies.
<]]>- MitchellWrite comment View comments
Selected publications:
- On the Lichtenbaum-Quillen conjectures from a stable homotopy-theoretic viewpoint (1994)
- Hypercohomology spectra and Thomason's descent theorem (1997)
<]]>- Mixed Hodge modulesWrite comment View comments
Elementary introduction by Saito in Asterisque 179-180
ICM talk 1990, by Saito I guess.
Schuermann on characteristic classes of mixed Hodge modules
arXiv:0907.0584 Characteristic classes of mixed Hodge modules. from arXiv Front: math.AG by Joerg Schuermann. This paper gives an introduction and overview about recent developments on the interaction of the theories of characteristic classes and mixed Hodge theory for singular spaces in the complex algebraic context. It uses M. Saito's deep theory of mixed Hodge modules as a "black box", thinking about them as "constructible or perverse sheaves of Hodge structures", having the same functorial calculus of Grothendieck functors. For the "constant Hodge sheaf", one gets the "motivic characteristic classes" of Brasselet-Schuermann-Yokura, whereas the classes of the "intersection homology Hodge sheaf" were studied by Cappell-Maxim-Shaneson.
There are two versions of these characteristic classes. The K-theoretical classes capture information about the graded pieces of the filtered de Rham complex of the filtered D-module underlying a mixed Hodge module. Application of a suitable Todd class transformation then gives classes in homology. These classes are functorial for proper pushdown and exterior products, together with some other properties one would expect for a "good" theory of characteristic classes for singular spaces. For "admissible variation of mixed Hodge structures" they have an explicit classical description in terms of "logarithmic de Rham complexes". On a point space they correspond to a specialization of the Hodge polynomial of a mixed Hodge structure, which one gets by forgetting the weight filtration.<]]>- Mixed Hodge structuresWrite comment View comments
Some articles of Wojtkowiak. A more fundamental paper is probably Deligne-Beilinson in Motives (Interpretation motivique...).
Some paper by Kashiwara.
Gelfand-Manin: Algebra V
http://mathoverflow.net/questions/73924/book-on-mixed-hodge-structures
<]]>- Model 2-categoryWrite comment View comments
- <]]>
- Model categoryWrite comment View comments
nLab Quillen equivalence
http://ncatlab.org/nlab/show/simplicial+model+category
http://ncatlab.org/nlab/show/cofibrantly+generated+model+category
http://mathoverflow.net/questions/16183/infty-1-categories-and-model-categories
Toen Essen talk: Any model category is naturally enriched over the homotopy cat of simplicial sets. This exposition is by the way a very concise intro to some key concepts in model cats, including localization and infinity-cat thinking, and homotopy limits.
http://ncatlab.org/nlab/show/global+model+structure+on+functors
http://mathoverflow.net/questions/78400/do-we-still-need-model-categories
References: Dwyer and Spalinski, Hovey's book, Goerss and Schemmerhorn.
Hirschhorn: Model cats and their localizations
Hirschhorn et al: Homotopy Limit Functors on Model Categories and Homotopical Categories (AMS)
Dwyer-Spalinski in the homotopy theory folder: Model categories, Homotopy limits brief intro, localization wrt a homology theory: very brief intro on p. 54.
Definition: A model category is a category
 with all small limits and colimits, together with a model structure on
with all small limits and colimits, together with a model structure on  . A model structure on a category consists of three subcategories, called cofibrations (cofibs), fibrations (fibs), and weak equivalences (WEs), and two functorial factorizations
. A model structure on a category consists of three subcategories, called cofibrations (cofibs), fibrations (fibs), and weak equivalences (WEs), and two functorial factorizations 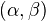 and
and 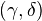 , satisfying:
, satisfying:- (2-out-of-3) If two of
 ,
,  ,
,  are WEs, then so is the third.
are WEs, then so is the third. - (Retracts) The three classes of morphisms are closed under retracts.
- (Lifting) Trivial cofibs have the LLP wrt fibs, and cofibs have the LLP wrt trivial fibs.
- (Factorization) For any morphism
 ,
, 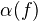 is a cofib,
is a cofib, 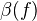 is a trivial fib,
is a trivial fib, 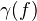 is a trivial cofib, and
is a trivial cofib, and 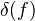 is a fib.
is a fib.
This is the definition given in Hovey, which differs slightly from earlier definitions, for example Quillen's original definition. Some people (ref?) have suggested that the first axiom should be replaced by a (4-out-of-6) axiom, to obtain a more general setting for homotopy theory in some cases.
Hovey suggests (p. 21) that the 2-category of model categories might behave like a model category.
Examples of model cats:
- Sset: Simplicial sets
- Top: Topological spaces
- Chain complexes of R-modules
- Modules over a Frobenius ring
- Cochain complexes of comodules over a Hopf algebra
See also nLab entry on homotopy theory
Christensen, Dwyer, Isaksen: Obstruction theory in model cats
It seems like all cofibrantly generated model cats are combinatorial: http://arxiv.org/abs/0905.0595
<]]>- (2-out-of-3) If two of
- Model category axiomsWrite comment View comments
Variants on model structure axioms (taken from Sevilla lectures): Baues, Brown, Cisinski, Thomason. See also Waldhausen category.
http://nlab.mathforge.org/nlab/show/Thomason+model+structure
http://mathoverflow.net/questions/29635/what-determines-a-model-structure
arXiv:1102.2512 Partial model categories and their simplicial nerves from arXiv Front: math.CT by C. Barwick, D. M. Kan In this note we consider partial model categories, by which we mean relative categories that satisfy a weakened version of the model category axioms involving only the weak equivalences. More precisely, a partial model category will be a relative category that has the two out of six property and admits a 3-arrow calculus.
We then show that Charles Rezk's result that the simplicial space obtained from a simplicial model category by taking a Reedy fibrant replacement of its simplicial nerve is a complete Segal space also holds for these partial model categories.We also note that conversely every complete Segal space is Reedy equivalent to the simplicial nerve of a partial model category and in fact of a homotopically full subcategory of a category of diagrams of simplicial sets.<]]>- Model category examplesWrite comment View comments
Lots of examples related to brave new rings are mentioned in here. Other, more standard examples:
A nonexample: (from Vezzosi lectures in Seville): there is no reasonable model structure on
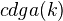 if k is a field of char p.
if k is a field of char p.Functor categories
One might ask in general about model structures on functor cats
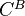 , where
, where  is a MC. If
is a MC. If 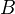 is so-called direct, can define WEs and fibrations objectwise, and get a model structure. If
is so-called direct, can define WEs and fibrations objectwise, and get a model structure. If 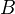 is so-called inverse, can define WEs and cofibs objectwise, and get a model structure. See Hovey 5.1 for details and properties. If
is so-called inverse, can define WEs and cofibs objectwise, and get a model structure. See Hovey 5.1 for details and properties. If 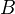 is a so-called Reedy category, can define a model structure by objectwise WEs, and a more complicated def of fibs and cofibs. See Hovey 5.2. Note that
is a so-called Reedy category, can define a model structure by objectwise WEs, and a more complicated def of fibs and cofibs. See Hovey 5.2. Note that 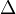 and its opposite are Reedy cats.
and its opposite are Reedy cats.Consider the category of functors from a category
 to
to  . We can define the projective model structure on this functor category as follows: WEs and fibrations are defined pointwise, while a cofibration is a "retract of a cellular inclusion" (see Dundas, p.40).
. We can define the projective model structure on this functor category as follows: WEs and fibrations are defined pointwise, while a cofibration is a "retract of a cellular inclusion" (see Dundas, p.40). See Weibel's obituary for Thomason - were these ideas ever written up?
http://nlab.mathforge.org/nlab/show/global+model+structure+on+functors
Simplicial sets
(Ref: Hovey). We define the set
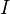 as the set of inclusions
as the set of inclusions 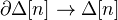 for
for 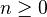 . Define
. Define  to be the set of inclusions
to be the set of inclusions 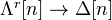 for
for 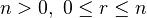 . A map
. A map  is a cofibration iff it is in
is a cofibration iff it is in 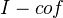 . A map is a (Kan) fibration iff it is in
. A map is a (Kan) fibration iff it is in 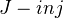 . A map
. A map  is a weak equivalence iff its geometric realization is a weak equivalence of topological spaces. The maps in
is a weak equivalence iff its geometric realization is a weak equivalence of topological spaces. The maps in 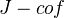 are called anodyne extensions.
are called anodyne extensions.From the definition, it follows that: A map is a cofibration iff it is injective. Hence every simplicial set is cofibrant. Also, every cofibration is a relative I-cell complex.
Thm: The category
 is a finitely generated model category with generating cofibrations I, generating trivial cofibrations J, and the above WEs. Same for pointed simplicial sets (fibs, cofibs, WEs are those in
is a finitely generated model category with generating cofibrations I, generating trivial cofibrations J, and the above WEs. Same for pointed simplicial sets (fibs, cofibs, WEs are those in  ).
).Simplicial groups, and simplicial groupoids
Topological spaces
A map
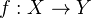 in
in 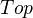 is a weak equivalence if
is a weak equivalence if 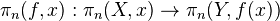
is an isomorphism for all
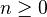 and all
and all 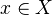 . Let
. Let 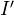 be the set of boundary inclusions
be the set of boundary inclusions 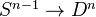 for all
for all 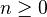 and let
and let 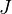 be the set of inclusions
be the set of inclusions 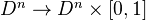 ,
, 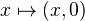 . We define a cofibration to be an element of
. We define a cofibration to be an element of 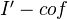 and a (Serre) fibration to be an element of
and a (Serre) fibration to be an element of 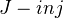 .
.Of course, every homotopy equivalence is a weak equivalence.
Theorem (Hovey p. 57): There is a finitely generated model structure on
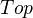 with
with 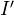 as the set of generating cofibrations, J as the set of generating trivial cofibrations, and the WEs as above. Every object of
as the set of generating cofibrations, J as the set of generating trivial cofibrations, and the WEs as above. Every object of 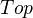 is fibrant, and the cofibrations are retracts of relative cell complexes.
is fibrant, and the cofibrations are retracts of relative cell complexes.There is a very similar statement for
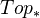 . There are also model structures on the category of k-spaces and on the category of compactly generated spaces, as well as on the pointed version of these cats. See Hovey pp. 58 for details.
. There are also model structures on the category of k-spaces and on the category of compactly generated spaces, as well as on the pointed version of these cats. See Hovey pp. 58 for details.See the last paragraph of this nLab entry and also this entry for other model structures on Top, e.g. the mixed model structure.
Chain complexes of comodules over a Hopf algebra
See Hovey, section 2.5.
Chain complexes of R-modules
We define a model structure on
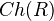 as follows. For any
as follows. For any 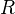 -module
-module 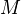 we define
we define 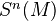 to be the complex with the module
to be the complex with the module 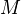 placed in degree
placed in degree  . We also define
. We also define 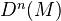 to be the complex with
to be the complex with 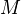 in degree
in degree  and
and 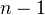 , and the identity as differential between them. Dropping
, and the identity as differential between them. Dropping 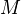 in this notation means that
in this notation means that  .
. Let
 be the set of evident injections
be the set of evident injections  , and let
, and let  be the maps
be the maps 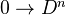 . Define a map to be a fibration if it is in
. Define a map to be a fibration if it is in 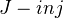 and a cofibration if it is in
and a cofibration if it is in 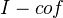 . As usual, a map is a WE if it induces an isomorphism on homology.
. As usual, a map is a WE if it induces an isomorphism on homology.From the above definition, it follows that a map is fibration if and only if it is surjective in each degree. A map is a trivial fibration iff it is in
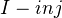 . If
. If  is a cofibrant chain complex, then
is a cofibrant chain complex, then 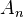 is projective for all
is projective for all  , and a bounded below complex of projectives is cofibrant. In general, a map is a cofibration iff it is a dimensionwise split inclusion with cofibrant cokernel.
, and a bounded below complex of projectives is cofibrant. In general, a map is a cofibration iff it is a dimensionwise split inclusion with cofibrant cokernel.See also nlab: http://www.ncatlab.org/nlab/show/model+structure+on+chain+complexes
Chain complexes of R-mods, with the injective model structure
Here is another model structure on
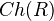 , called the injective model structure. We define a map to be an injective fibration if it has the RLP wrt all maps that are both injections and WEs.
, called the injective model structure. We define a map to be an injective fibration if it has the RLP wrt all maps that are both injections and WEs. Theorem: The injections, injective fibrations, and WEs are part of a cofibrantly generated model structure on
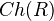 . The injective fibrations are the surjections with fibrant kernel. Every fibrant object is a complex of injectives. Every bounded above complex of injectives is fibrant. The injective trivial fibrations are the surjections with injective kernel; a complex is injective iff it is fibrant and acyclic.
. The injective fibrations are the surjections with fibrant kernel. Every fibrant object is a complex of injectives. Every bounded above complex of injectives is fibrant. The injective trivial fibrations are the surjections with injective kernel; a complex is injective iff it is fibrant and acyclic.Modules over a quasi-Frobenius ring
A ring
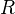 is called quasi-Frobenius if the projective and injective
is called quasi-Frobenius if the projective and injective 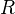 -modules coincide. Examples include the group ring of a finite group over a field. For such a ring, there is a cofibrantly generated model structure on
-modules coincide. Examples include the group ring of a finite group over a field. For such a ring, there is a cofibrantly generated model structure on 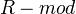 where the cofibrations are the injections, the fibrations are the surjections, and the WEs are the "stable equivalences".
where the cofibrations are the injections, the fibrations are the surjections, and the WEs are the "stable equivalences".Chain complexes of sheaves
See Hovey
Categories
http://www.ncatlab.org/nlab/show/Thomason+model+structure
http://front.math.ucdavis.edu/0907.5339 Tanaka on a new model str for Cat.
Algebras over an operad
Categories
I think Cat can be equipped with a model structure. See isofibration on nLab
Something related to Lie groups
G-spectra? See K0407 and K0408
Other examples
J.F. Jardine, "A closed model structure for differential graded algebras", Cyclic Cohomology and Noncommutative Geometry, Fields Institute Communications, Vol. 17, AMS (1997), 55-58.
MR764018 Golasinski: Model structures on
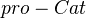 and
and 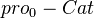
Larusson on equivalence relations
nLab entries on model structure: Model cat, and various entries beginning with model structure on
For model structure on DG-algebras, see Gelfand and Manin: Methods of homological algebra, Chapter 5
Simplicial groupoids, see Dwyer: Homotopy th and simplicial groupoids. See also http://www.ncatlab.org/nlab/show/model+structure+on+presheaves+of+simplicial+groupoids
Pointed simplicial spaces, see Dwyer-Kan-Stover paper, as well as its review for a comparison with Reedy structure.
Isaksen has a few papers on limits and model structures on pro-cats. In particular, for any proper model category C he produces a model structure on pro-C. I don't have these papers electronically, but they probably exist.
Harper: Homotopy theory of modules over operads etc. ArXiv. This paper studies the existence of model category structures on algebras and modules over operads in monoidal model categories.
Larusson: The cat of complex manifolds can be embedded into a model cat in a way such that a manifold is cofibrant iff it is Stein, and fibrant iff it is Oka. See AMS Notice Jan 2010: What is an Oka manifold. Original article not referenced.
Ostvaer stuff on Cstar-algebras
<]]>- Model category examples 2Write comment View comments
http://www.ncatlab.org/nlab/show/model+structure+on+homotopical+presheaves
http://mathoverflow.net/questions/98982/non-noetherian-stable-homotopy
Title: Degreewise n-projective and n-flat model structures on chain complexes Authors: Marco Pérez. http://front.math.ucdavis.edu/1204.1358
<]]>- Model category IIWrite comment View comments
http://mathoverflow.net/questions/59756/model-category-structure-on-categories-enriched-over-quasi-coherent-sheaves mentions some general ideas of Tapia
http://mathoverflow.net/questions/56166/do-homotopy-groups-always-commute-with-filtered-colimits discusses model structures on symmetric spectra and related categories, with some useful facts on combinatorial model structures and Cisinski's framework.
http://mathoverflow.net/questions/52508/strom-type-model-structure-on-chain-complexes
http://mathoverflow.net/questions/42755/non-standard-model-category-structure-on-cochain-complexes
http://mathoverflow.net/questions/107030/relationships-between-properties-of-model-categories
Model structures for simplicial presheaves: see the appendix to Panin-Pimenov-Roendigs
<]]>- Model siteWrite comment View comments
See Toen: Essen talk. Section 4, in particular pp 30 I think. This includes a great discussion on model topologies, and stacks over model sites.
<]]>- Model stackWrite comment View comments
- <]]>
- Model theoryWrite comment View comments
There is at least one introductory Springer book.
Folder: AG/Model theory. Includes the MSRI 39 volume with various survey articles.
http://en.wikipedia.org/wiki/Model_theory
Book: A course in model theory, Poizat
<]]>- Model toposWrite comment View comments
Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Mentions Segal topoi briefly.
Many things in writings by Toen and Vezzosi on HAG, see refs under Homotopical algebraic geometry
Toen: Segal topoi and stacks over Segal categories. File Toen web prepr msri.pdf. Analogous and in some sense equivalent to the notion of model topos, but some advantages. Includes a Giraud type statement characterizing Segal topoi among Segal cats. Notion of homotopy type of a Segal site, improving on the etale homotopy theory of schemes, and more generally on the theory of homotopy types of sites as defined by Artin and Mazur.
http://ncatlab.org/nlab/show/model+structure+on+SSet-enriched+presheaves this is probably relevant
<]]>- ModelsWrite comment View comments
Try to ask Tony.
Email from Thomas Riepe:
Conc. 1-motives, I'd recommend the appendix of Milne's book "Arithmetic Duality Theorems" for the background on biextensions and Neron models, for biextensions probably further Mumford's nice article and the references Milne makes. For Neron models, IMO one does not need to know the details, so Artin's article on them in "Arithm. Geometry" may be enough (for more I'd recommend Bosch etc.'s book).
http://mathoverflow.net/questions/416/existence-of-smooth-models
Neron model: Book by Bosch et al under Ell curves folder
<]]>- Modular curveWrite comment View comments
Modular curves over Spec Z are covered in GEOMETRIC MODULAR FORMS AND ELLIPTIC CURVES by Haruzo Hida.
arXiv:1003.1935 The Langlands-Kottwitz approach for the modular curve from arXiv Front: math.AG by Peter Scholze We show how the Langlands-Kottwitz method can be used to determine the local factors of the Hasse-Weil zeta-function of the modular curve at places of bad reduction. On the way, we prove a conjecture of Haines and Kottwitz in this special case.
http://mathoverflow.net/questions/51147/what-objects-do-the-cusps-of-modular-curve-classify
arXiv:0909.0714 Higher order modular forms and mixed Hodge theory from arXiv Front: math.AG by Ramesh Sreekantan In this paper we introduce a certain space of higher order modular forms of weight 0 and show that it has a Hodge structure coming from the geometry of the fundamental group of a modular curve. This generalizes the usual structure on classical weight 2 forms coming from the cohomology of the modular curve. Further we construct some higher order Poincaré series to get higher order higher weight forms and using them we define a space of higher weight, higher order forms which has a mixed Hodge structure as well.
arXiv:1209.0046 The Geometry of Hida Families and \Lambda-adic Hodge Theory from arXiv Front: math.NT by Bryden Cais We construct \Lambda-adic de Rham and crystalline analogues of Hida's ordinary \Lambda-adic etale cohomology, and by exploiting the geometry of integral models of modular curves over the cyclotomic extension of \Q_p, we prove appropriate finiteness and control theorems in each case. We then employ integral p-adic Hodge theory to prove \Lambda-adic comparison isomorphisms between our cohomologies and Hida's etale cohomology. As applications of our work, we provide a "cohomological" construction of the family of (\phi,\Gamma)-modules attached to Hida's ordinary \Lambda-adic etale cohomology by Dee, and we give a new and purely geometric proof of Hida's finitenes and control theorems. We are also able to prove refinements of theorems of Mazur-Wiles and of Ohta; in particular, we prove that there is a canonical isomorphism between the module of ordinary \Lambda-adic cuspforms and the part of the crystalline cohomology of the Igusa tower on which Frobenius acts invertibly.
arXiv:1205.5896 Approximate computations with modular curves fra arXiv Front: math.AG av Jean-Marc Couveignes, Bas Edixhoven This article gives an introduction for mathematicians interested in numerical computations in algebraic geometry and number theory to some recent progress in algorithmic number theory, emphasising the key role of approximate computations with modular curves and their Jacobians. These approximations are done in polynomial time in the dimension and the required number of significant digits. We explain the main ideas of how the approximations are done, illustrating them with examples, and we sketch some applications in number theory.
<]]>- Modular formWrite comment View comments
See docs in modular forms folder
http://mathoverflow.net/questions/74775/motive-of-a-modular-form
http://mathoverflow.net/questions/79868/what-does-mellin-inversion-really-mean
<]]>- Modular varietiesWrite comment View comments
arXiv:0907.5263 Geometry of the Siegel modular threefold with paramodular level structure from arXiv Front: math.AG by Chia-Fu Yu In this paper we extend some results of Norman and Oort and of de Jong, and give an explicit description of the geometry of the Siegel modular threefold with paramodular level structure. We also discuss advantages and restrictions of three standard methods for studying moduli spaces of abelian varieties.
Matthias Schuett has at least one arxiv preprint on modularity of some higher-dimensional varieties.
[arXiv:1212.4308] Modularity of Calabi--Yau varieties: 2011 and beyond from arXiv Front: math.NT by Noriko Yui This paper presents the current status on modularity of Calabi-Yau varieties since the last update in 2003. We will focus on Calabi-Yau varieties of dimension at most three. Here modularity refers to at least two different types: arithmetic modularity and geometric modularity. These will include: (1) the modularity (automorphy) of Galois representations of Calabi-Yau varieties (or motives) defined over Q or number fields, (2) the modularity of solutions of Picard--Fuchs differential equations of families of Calabi-Yau varieties, and mirror maps (mirror moonshine), (3) the modularity of generating functions of invariants counting certain quantities on Calabi-Yau varieties, and (4) the modularity of moduli for families of Calabi-Yau varieties.
http://mathoverflow.net/questions/72951/arithmetic-and-moduli-spaces-of-higher-genus-curves
http://front.math.ucdavis.edu/1110.0106 mentions modularity conjectures for som threefold
<]]>- ModularityWrite comment View comments
Gouvea and Yui on modularity of rigid CY 3-folds.
arXiv:0908.1210 a detailed account is given of a patching argument due to Serre that proves that the modularity of all rigid Calabi-Yau threefolds defined over the rationals follows from Serre's modularity conjecture. In this note (a letter to N. Yui) we give an alternative proof of this implication. The main difference with Serre's argument is that instead of using as main input residual modularity in infinitely many characteristics we just require residual modularity in a suitable characteristic. This is combined with effective Cebotarev.
See a chapter in Global aspects of Complex Geometry, in Complex manifolds or Conferences folder
<]]>- ModuleWrite comment View comments
http://mathoverflow.net/questions/100565/why-are-ring-actions-much-harder-to-find-than-group-actions
<]]>- Module over a monoidal categoryWrite comment View comments
A right module
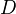 over a monoidal category
over a monoidal category  is a a functor
is a a functor 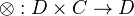 together with two natural IMs expressing the obvious associativity and unit conditions. These must satisfy three coherence diagrams. Often we refer to these as just
together with two natural IMs expressing the obvious associativity and unit conditions. These must satisfy three coherence diagrams. Often we refer to these as just  -modules.
-modules.Example: Any category with all coproducts is a module over Set, if we take
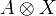 to be the coproduct of
to be the coproduct of  with itself
with itself 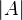 times.
times.Can define functor of
 -modules, requiring it to commute with the tensor up to natural isomorphism, and satisfy two coherence diagrams. Get a 2-category of C-modules.
-modules, requiring it to commute with the tensor up to natural isomorphism, and satisfy two coherence diagrams. Get a 2-category of C-modules.Example: A functor of Set-modules is a functor preserving coproducts.
See also Algebra over a monoidal category
Recall that
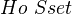 is a closed symmetric monoidal category. Hovey proves in chapter 5 that the homotopy category of any model category is naturally a closed
is a closed symmetric monoidal category. Hovey proves in chapter 5 that the homotopy category of any model category is naturally a closed 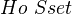 -module. This implies that results about simplicial model cats often can be transferred to any model category. Also, the homotopy category of a monoidal MC is naturally a closed
-module. This implies that results about simplicial model cats often can be transferred to any model category. Also, the homotopy category of a monoidal MC is naturally a closed 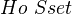 -algebra. The proof of these results uses simplicial and cosimplicial resolutions of objects in a model category, model structures on functor cats to a MC, Reedy categories, framings, latching space, matching space.<]]>
-algebra. The proof of these results uses simplicial and cosimplicial resolutions of objects in a model category, model structures on functor cats to a MC, Reedy categories, framings, latching space, matching space.<]]>- Module over a monoidal MCWrite comment View comments
Let
 be a monoidal model category. A
be a monoidal model category. A  -model category is a
-model category is a  -module
-module 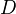 with a model structure such that the following conditions hold:
with a model structure such that the following conditions hold:- The action map
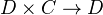 is a Quillen bifunctor.
is a Quillen bifunctor. - The map
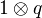 is a WE for all cofibrant
is a WE for all cofibrant  . Here
. Here 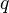 is cofibrant replacement of unit, and
is cofibrant replacement of unit, and 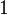 is the identity on
is the identity on  . This is automatic when the unit is cofibrant.
. This is automatic when the unit is cofibrant.
A
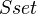 -model category is called a simplicial model category. This def is different from Quillen's. For Quillen, Top is a simplicial MC, but not with this def. The cateogries
-model category is called a simplicial model category. This def is different from Quillen's. For Quillen, Top is a simplicial MC, but not with this def. The cateogries 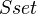 , k-spaces, CG spaces and their pointed versions are all simplicial MCs, but categories of chain complexes are not. However,
, k-spaces, CG spaces and their pointed versions are all simplicial MCs, but categories of chain complexes are not. However, 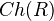 is a
is a 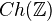 -model category.
-model category.If
 is pointed, then so is every
is pointed, then so is every  -model category as well. Under some conditions, if
-model category as well. Under some conditions, if 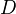 is a
is a  -model caat, then
-model caat, then 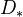 is a
is a 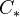 -model category. Get equivalence between pointed
-model category. Get equivalence between pointed  -model cats and
-model cats and 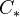 -model cats.
-model cats.Can also define algebras: Let
 be as above. A monoidal
be as above. A monoidal  -model category is a monoidal model category
-model category is a monoidal model category 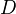 together with a monoidal Quillen functor
together with a monoidal Quillen functor 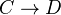 . Get a 2-category again.
. Get a 2-category again.Example: k-spaces is a symmetric monoidal
 -model category.<]]>
-model category.<]]>- The action map
- Module spectraWrite comment View comments
arXiv:1108.6309 On the Algebraic Classification of Module Spectra from arXiv Front: math.KT by Irakli Patchkoria Using methods developed by Franke, we obtain algebraic classification results for modules over certain symmetric ring spectra ($S$-algebras). In particular, for any symmetric ring spectrum $R$ whose graded homotopy ring $\pi*R$ has graded global homological dimension 2 and is concentrated in degrees divisible by some natural number $N \geq 4$, we prove that the homotopy category of $R$-modules is equivalent to the derived category of the homotopy ring $\pi*R$. This improves the Bousfield-Wolbert algebraic classification of isomorphism classes of objects of the homotopy category of $R$-modules. The main examples of ring spectra to which our result applies are the $p$-local real connective $K$-theory spectrum $ko_{(p)}$, the Johnson-Wilson spectrum E(2), and the truncated Brown-Peterson spectrum $BP<1>$, for an odd prime $p$.
<]]>- Moduli of curvesWrite comment View comments
A great book is Albarello-Cornalba-Griffiths vol 2.
http://ncatlab.org/nlab/show/Mumford+class contains some good references.
arXiv:1109.2173 GIT Constructions of Log Canonical Models of Mg from arXiv Front: math.AG by Jarod Alper, Donghoon Hyeon The purpose of this article is to give an overview of the construction of moduli spaces of curves from the viewpoint of the log minimal model program for Mg by providing an update of recent developments and discussing future problems. This survey is distinguished from the recent articles of Fedorchuk-Smyth and Morrison in its focus on low degree Hilbert stability of curves.
<]]>- Moduli of vector bundlesWrite comment View comments
A name: Ramanan?
http://ncatlab.org/nlab/show/moduli+space+of+bundles
See Toen Essen talk for the idea of a derived moduli stack of VBs. Also derived moduli stack of stable maps, with applications to Gromov-Witten theory, see p 4. Local rings of derived moduli spaces should be cdgas.
<]]>- Moduli spacesWrite comment View comments
Many things in folder AG/Moduli
http://mathoverflow.net/questions/13868/proper-definition-of-a-moduli-problem
arXiv:1004.3259 Open problems (for AGNES) from arXiv Front: math.AG by R. Pandharipande The article contains a few questions and speculations related to the moduli spaces of curves, K3 surfaces, maps, and sheaves presented in the problem session of the AGNES conference in Amherst (April 2010).
Harris: An introduction to the moduli space of curves
Harris and M?: Moduli of curves
Arithmetic moduli of elliptic curves, by Katz and Mazur
http://nlab.mathforge.org/nlab/show/moduli+space
What about good refs for moduli of vector bundles?
Two books to be published by CUP in 2009: Bradlow et al: Moduli spaces of VBs, Huybrechts and Lehn: The Geometry of Moduli spaces of sheaves.
Ramanan et al ed, Moduli spaces and VBs, LMS lecture note series
In general, what kind of objects can be described by moduli spaces? Curves and VBs, maybe cycles/subvarieties. What else??? Metrics? t-structures (Bridgeland)?
Bridgeland says in the intro of Fourier-Mukai transforms for K3 and elliptic fibrations, that we know quite a lot about moduli of stable VBs on projective surfaces, but not so much about VBs on higher-dimensional varieties. The paper tries to do something about this in certain cases I think.
Blanc, Dwyer, Goerss: The realization space of a Pi-algebra. Studies the moduli space of spaces with a fixed structured homotopy groups. It is defined as the classifying space of the category whose objects are such top spaces, and morphisms are weak equivalences. Description in terms of a tower. These methods might apply to other moduli problems.
There are various papers by Olsson et al, not downloaded.
arXiv:1008.0621 Moduli of varieties of general type from arXiv Front: math.AG by János Kollár This is a survey paper discussing the moduli problem for varieties of general type.
About moduli for higher-dimensional varieties: Toen and Anel prove that the number of iso classes of smooth projective complex alg vars with the same derived cat must be countable. File Toen web publ dgcat-alg.pdf. They use some kind of (nonalgebraic) stack which in some sense is a moduli space for smooth projective varieties.
arXiv:0908.1938 Stability phenomena in the topology of moduli spaces from arXiv Front: math.AT by Ralph L. Cohen The recent proof by Madsen and Weiss of Mumford's conjecture on the stable cohomology of moduli spaces of Riemann surfaces, was a dramatic example of an important stability theorem about the topology of moduli spaces. In this article we give a survey of families of classifying spaces and moduli spaces where "stability phenomena" occur in their topologies. Such stability theorems have been proved in many situations in the history of topology and geometry, and the payoff has often been quite remarkable. In this paper we discuss classical stability theorems such as the Freudenthal suspension theorem, Bott periodicity, and Whitney's embedding theorems. We then discuss more modern examples such as those involving configuration spaces of points in manifolds, holomorphic curves in complex manifolds, gauge theoretic moduli spaces, the stable topology of general linear groups, and pseudoisotopies of manifolds. We then discuss the stability theorems regarding the moduli spaces of Riemann surfaces: Harer's stability theorem on the cohomology of moduli space, and the Madsen-Weiss theorem, which proves a generalization of Mumford's conjecture. We also describe Galatius's recent theorem on the stable cohomology of automorphisms of free groups. We end by speculating on the existence of general conditions in which one might expect these stability phenomena to occur.
<]]>- Moduli stacksWrite comment View comments
An excellent introduction to derived AG is the CRM 2008 notes, in Toen web unpublished folder. These notes also covers algebraic stacks, the idea of moduli spaces, a little about cotangent complexes, and examples of derived algebraic stacks.
<]]>- MonadWrite comment View comments
A monad (also called a triple), is a functor together with two natural transformations, satisfying certain conditions. See Wikipedia.
For basic notions, including modules over a monad, see Fresan's survey of Durov's work
http://mathoverflow.net/questions/55182/what-is-known-about-the-category-of-monads-on-set
http://mathoverflow.net/questions/19038/right-actions-of-operads-and-monads
nlab algebraic monad
http://ncatlab.org/nlab/show/comonad
http://ncatlab.org/nlab/show/monadic+adjunction
<]]>- MonodromyWrite comment View comments
Folder: AG/Singularities and monodromy
For some kind of "higher monodromy", see Toen: Vers une interpretation galoisienne etc. File Toen web publ gal.pdf.
http://ncatlab.org/nlab/show/monodromy
http://rigtriv.wordpress.com/2010/02/25/monodromy-representations/
http://rigtriv.wordpress.com/2010/03/02/monodromy-and-moduli/
<]]>- MonoidWrite comment View comments
http://mathoverflow.net/questions/430/homological-algebra-for-commutative-monoids
"John, the monoid analogue of a long exact sequence is probably a simplicial monoid that is contractible (as a simplicial set), or something like that." (James Borger on MO)
<]]>- Monoidal categoryWrite comment View comments
Want to define rings and the like in the 2-category of cats and functors, and also in the 2-category of cats and adjunction. The algebraic notions of ring, commutative ring, modules over a ring, algebras over a ring, and central commutative algebras over a commutative ring, correspond to: monoidal category, symmetric monoidal category, modules over a monoidal category, algebras over a monoidal category, and central symmetric algebra over a symmetric monoidal category. If we consider adjunctions instead of functors, we add the word "closed" to each of these terms.
Def: A monoidal structure on a category
 is a "tensor product" bifunctor
is a "tensor product" bifunctor 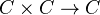 , a unit object
, a unit object 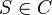 , a natural associativity isomorphism, and two natural (left and right) unit IMs, satisfying three coherence diagrams. A category with such a structure is called a monoidal category. Def of monoidal functor (essentially has to preserve unit and product up to a natural isomorphism), monoidal natural transformation, and of the 2-category of monoidal cats.
, a natural associativity isomorphism, and two natural (left and right) unit IMs, satisfying three coherence diagrams. A category with such a structure is called a monoidal category. Def of monoidal functor (essentially has to preserve unit and product up to a natural isomorphism), monoidal natural transformation, and of the 2-category of monoidal cats.Examples: Sets, with Cartesian product. Topological spaces, with product. Simplicial sets, with product. Modules over a commutative ring, with tensor product. (All these are actually symmetric monoidal.)
Examples of monoidal functors: The free R-module functor from Sets to R-mods. The geometric realization functor.
Whenever
 is monoidal, this is also the case for
is monoidal, this is also the case for 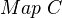 . (See Hovey p. 109)<]]>
. (See Hovey p. 109)<]]>- Monoidal model categoryWrite comment View comments
A monoidal MC is like a ring in the 2-category of MCs.
Examples: Simplicial sets, pointed simplicial sets, chain complexes of modules over a commutative ring, chain complexes of comodules over a commutative Hopf algebra, k-spaces, compactly generated topological spaces. Non-example: Topological spaces.
Def: A monoidal category is a closed category
 , with a model structure, such that the following holds:
, with a model structure, such that the following holds: - The monoidal structure is a Quillen bifunctor
- Let
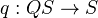 be a cofibrant replacement for the unit
be a cofibrant replacement for the unit  . Then the natural map
. Then the natural map 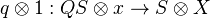 is a WE for all cofibrant
is a WE for all cofibrant  , and same for
, and same for 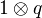 . (This is automatic if
. (This is automatic if  is cofibrant.)
is cofibrant.)
Similarly, can define symmetric monoidal model category.
Example:
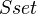 is a symmetric monoidal model category, and same for
is a symmetric monoidal model category, and same for 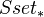 . For any (symmetric) monoidal model category with cofibrant unit coinciding with the terminal object, the model category
. For any (symmetric) monoidal model category with cofibrant unit coinciding with the terminal object, the model category 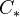 is also (symmetric) monoidal. CG spaces and k-spaces form symmetric monoidal model cats under the k-space product, and same for the pointed versions. Unbounded chain complexes of R-mods is a symmetric monoidal model category (using the standard model structure, not the injective one). Chain complexes of comodules over a commutative Hopf algebra over a field also form a SMMC. The model category R-mod is monoidal, if R is a quasi-Frobenius ring and a finitedimensional Hopf algebra over a field. It is symmetric iff R is cocommutative.
is also (symmetric) monoidal. CG spaces and k-spaces form symmetric monoidal model cats under the k-space product, and same for the pointed versions. Unbounded chain complexes of R-mods is a symmetric monoidal model category (using the standard model structure, not the injective one). Chain complexes of comodules over a commutative Hopf algebra over a field also form a SMMC. The model category R-mod is monoidal, if R is a quasi-Frobenius ring and a finitedimensional Hopf algebra over a field. It is symmetric iff R is cocommutative.In the above examples the unit is cofibrant. The category of S-modules is a monoidal model category in which the unit is not cofibrant.
Hovey: "It is essential that
 is a closed monoidal category for
is a closed monoidal category for 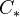 to be monoidal. For example, the smash product on pointed topological spaces fails to be associative". "
to be monoidal. For example, the smash product on pointed topological spaces fails to be associative". "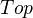 is not a monoidal model category, because it is not a closed monoidal category".
is not a monoidal model category, because it is not a closed monoidal category".Given two monoidal MCs, a monoidal Quillen adjunction between them is a Quillen adjunction
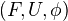 such that
such that  is a monoidal functor, and
is a monoidal functor, and  applied to cofibrant replacement of the unit is a WE. The last condition is redundant when the unit is cofibrant, but necessary in general to ensure that the unit isomorphism passes to the homotopy category. The left adjoint above is referred to as a monoidal Quillen functor. We get a 2-category of monoidal MCs, and can also construct the 2-category of symmetric monoidal MCs, with symmetric monoidal Quillen functors.
applied to cofibrant replacement of the unit is a WE. The last condition is redundant when the unit is cofibrant, but necessary in general to ensure that the unit isomorphism passes to the homotopy category. The left adjoint above is referred to as a monoidal Quillen functor. We get a 2-category of monoidal MCs, and can also construct the 2-category of symmetric monoidal MCs, with symmetric monoidal Quillen functors.Example: Adding a disjoint basepoint is a symmetric monoidal Quillen functor from
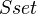 to
to 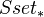 , whose right adjoint is the forgetful functor. Similarly for k-spaces and CG spaces. Geometric realization is a symmetric monoidal Quillen functor from (pointed) simplicial sets to (pointed) k-spaces.
, whose right adjoint is the forgetful functor. Similarly for k-spaces and CG spaces. Geometric realization is a symmetric monoidal Quillen functor from (pointed) simplicial sets to (pointed) k-spaces.The homotopy category
Recall (Hovey p. 106) the definition of an adjunction in two variables.
Theorem: Suppose
 is a (symmetric) monoidal model category. Then its homotopy category can be given the structure of a closed (symmetric) monoidal category. The adjunction of two variables
is a (symmetric) monoidal model category. Then its homotopy category can be given the structure of a closed (symmetric) monoidal category. The adjunction of two variables 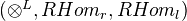 that is part of the closed structure on
that is part of the closed structure on 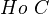 is the total derived adjunction of
is the total derived adjunction of 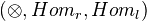 . The associativity, unit (and commutativity) IMs on
. The associativity, unit (and commutativity) IMs on  are derived from the corresponding IMs of
are derived from the corresponding IMs of 
We make this more precise, and give the statement for the more structured monoidal model cats. Let
 be a fixed monoidal model category.
be a fixed monoidal model category.Thm: The pseudo-2-functor
 from model cats to
from model cats to  lifts to a pseudo-2-functor:
lifts to a pseudo-2-functor:- from monoidal model cats to closed monoidal cats
- from symmetric monoidal model cats to closed symmetric monoidal cats
- from
 -model cats to closed
-model cats to closed  -modules
-modules - from monoidal
 -model cats to closed
-model cats to closed 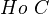 -algebras
-algebras - from symmetric (resp. central) monoidal
 -model cats to closed symmetric (resp. central)
-model cats to closed symmetric (resp. central) 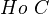 -algebras (if
-algebras (if  is symmetric)
is symmetric)
<]]>- Moore spaceWrite comment View comments
- <]]>
- MoravaWrite comment View comments
- <]]>
- Morava ideasWrite comment View comments
- <]]>
- Mordell conjectureWrite comment View comments
Review of a seminar in Paris. See also the othere refs at the end of the review.
Bourbaki seminar by Szpiro: review
Asterisque 127: Seminar on arithmetic bundles: The Mordell conjecture
http://front.math.ucdavis.edu/0912.4325 Notes by Parshin and Zarhin on finiteness problems in arithmetic geometry. See also Manin-Panchiskin for good stuff on this.
Vojta: Mordell's conjecture over function fields. In Inventiones Vol 98 no 1.
http://mathoverflow.net/questions/56011/why-should-i-believe-the-mordell-conjecture
<]]>- Mordell-Lang conjectureWrite comment View comments
arXiv:1103.2625 On some questions raised by Anand Pillay and Franck Benoist from arXiv Front: math.AG by Damian Rössler We prove that indefinitely $p$-divisible points on abelian varieties defined over function fields of transcendance degree one over a finite field are necessarily torsion points. We also prove that when the endomorphism ring of the abelian variety is $\mZ$ then there are no indefinitely $p$-divisible points of order a power of $p$. Finally, we prove a general result on the sparsity of points in a special fibre of an abelian variety as above, which lift to highly $p$-divisible unramified points; we show how it can be used to give a new proof of the Mordell-Lang conjecture for ordinary abelian varieties.
<]]>- Mordell-Weil theoremWrite comment View comments
- <]]>
- MorelWrite comment View comments
Publications/preprints:
- The Homotopy T-Structure of the Stable Homotopy Category of Schemes; seems to have disappeared
<]]>- Mori programWrite comment View comments
arXiv:1009.3188 New outlook on Mori theory, I from arXiv Front: math.AG by Paolo Cascini, Vladimir Lazic We give a simple and self-contained proof of the finite generation of adjoint rings with big boundaries. As an easy consequence, we show that the canonical ring of a smooth projective variety is finitely generated.
arXiv:1005.0614 New outlook on Mori theory, II from arXiv Front: math.AG by Alessio Corti, Vladimir Lazic In this note we prove that all the fundamental theorems of Mori theory follow quickly from the finite generation of adjoint rings with big boundaries, which was recently proved by a self-contained argument based on extension theorems and induction on the dimension. Thus, we give a new and more efficient organization of higher dimensional algebraic geometry.
<]]>- Morita theoryWrite comment View comments
Toen: The homotopy theory of dg-cats and derived Morita theory. File Toen web publ mapdgcat.pdf.
Chapter 6 of Anderson and Fuller, in Homol alg folder
Chapter 7 of Lam: Lectures on modules and rings. In Homol alg folder
Title: Flat Model Structures for Nonunital Algebras and Higher K-Theory. Authors: S. Estrada and P.A. Guil-Asensio. We prove the existence of a Quillen Flat Model Structure in the category of unbounded complexes of h-unitary modules over a nonunital ring (or a $k$-algebra, with $k$ a field). This model structure provides a natural framework where a Morita-invariant homological algebra for these nonunital rings. http://arxiv.org/abs/0906.4735
Morita theory: Borceaux vol 2 pp 180. Two rings are Morita equivalent if their categories of right modules are equivalent. Can define Morita equivalence more generally for algebraic theories other than rings. If R is commutative with unit, then R and and the ring of nxn square matrices over R are Morita equiv. Two things with unit which are Morita equiv have isomorphic centres. Two commutative rings with unit are Morita equiv iff they are isomorphic.
See also Weibel for Morita equiv.
<]]>- Morphism of schemesWrite comment View comments
Maybe make a table with overview. Possible sources: FGA book.
Many notions, such as smooth, flat, etale, proper, open immersion, can be defined in the much more general contexts of Toen. See for example HAG II, the Barcelona notes, and the Brave new algebraic geometry paper.
http://mathoverflow.net/questions/15474/functorial-characterization-of-morphisms-of-schemes
From review of Murre lectures on fundamental gp: A flat morphism is open. A faithfully flat morphism is an effective epimorphism.
For reference, we collect here some basic definitions of various kinds of morphisms of schemes.
Projective
Smooth
Quasi-projective
Finite type
Open
Proper
Separated
Local complete intersection
"E.g. any morphism between smooth k-schemes"
<]]>- MorseWrite comment View comments
Collected works/papers, 6 volumes. Also Selected papers, 1 vol.
<]]>- Morse theoryWrite comment View comments
Morse theory: See Morse theory folder
<]]>- Motivic Chow seriesWrite comment View comments
arXiv:0909.5232 Rationality of motivic Chow series modulo A^1-homotopy from arXiv Front: math.AG by E. Javier Elizondo, Shun-ichi Kimura Consider the formal power series $\sum [C{p, \alpha}(X)]t^{\alpha}$ (called Motivic Chow Series), where $Cp(X)=\disjoint C{p, \alpha}(X)$ is the Chow variety of $X$ parametrizing the $p$-dimensional effective cycles on $X$ with $C{p, \alpha}(X)$ its connected components, and $[C{p, \alpha}(X)]$ its class in $K(ChM){A^1}$, the $K$-ring of Chow motives modulo $A^1$ homotopy. Using Picard product formula and Torus action, we will show that the Motivic Chow Series is rational in many cases.
<]]>- Motivic Galois groupsWrite comment View comments
See Serre in Motives vol, or Chapter 6 in André
See Toen AIM talk on Homotopy types of algebraic varieties, for a unified viewpoint on extra structure on Weil cohomology theories, and more.
<]]>- Motivic homotopy theoryWrite comment View comments
A standard reference is Morel-Voevodsky: A1-homotopy theory of schemes. Starts out with general theory of simplicial sheaves, then A1-homotopy theory. Read this properly some day. Among many other things, they describe ("real and complex") realization functors, relating the A1-homotopy cat to classical homotopy theory.
An introduction is found in Voevodsky's Seattle lectures, probably on the webpage of Weibel, otherwise in Voevodsky folder.
http://mathoverflow.net/questions/2520/homotopy-theory-of-schemes-examples
http://mathoverflow.net/questions/2694/formalism-of-homotopy-theory-of-schemes
Voevodsky's Nordfjordeid lecture - supernice (Voevodsky folder). Working over a field unfortunately. Basic constructions, of SH etc. Brief discussion of Thom spaces and homotopy purity. Cohomology theories: the motivic EM spectrum, KGL, MGL, claim that the notions of orientation and FGLs have direct analogs for P1-spectra. The slice filtration (great intro), update on Open problems paper. The zero-th slice of the unit spectrum is HZ, this is known for fields of char zero. Brief discussion of AHSS. Appendix on the Nisnevich topology, Nisnevich descent, and model structures.
Voevodsky ICM talk summary: Starting with a cat C, can use homotopy theory to study it, if we embed it into a bigger nicer cat of spaces, with a notion of weak equiv. Can then define the homotopy cat of spaces, and also the SW cat (naively stabilizing suspension), and better: a stable homotopy cat, using spectra. The second approach gives existence of infinite direct sums, so that rep theorems can be applied. Can carry out this starting with Sm/S for any notherian base, and then define motivic cohomology, alg Kth and alg cobord on this cat for any such S. Spaces are Nisnevich sheaves of sets, and there is a notion of space of finite type, which implies categorical compactness. Model structure. Almost fibrant vs quasifibrant: probably EM spaces are the latter only. SW cat and various spheres. MV, Gysin, and blowup loch exact sequences. The Gysin les comes from a closed embedding of smooth schemes, and involves the Thom space of the normal bundle. The blowup sequence here is also for a closed embedding of smooth schemes. Prop 5.5: SH is compactly generated. Specialize to the case of T=P1. Get same long exact seqs. Chapter 6: For any E in SH, can define a corresponding cohomology and homology theory. Any such theory has Gysin, MV, and blowup long exact sequences. Usefulness of a "Brown rep thm" is restricted by the fact that it seems like the statement would be about functors on spaces, or spaces of finite type, and not functors on schemes. Now to EM spaces: Naive idea does not work. Instead, use idea of Suslin: use Dold-Thom thm. The right analogue of Symm is described, using finite correspondences I think. More details and def of the motivic cohomology spectrum. Def of BGL, i.e. the alg K-theory spectrum, and comparison statements. Also MGL (alg cobordism). Two future directions: one related to circumventing problems related to RoS and hence restrictions to char zero base field, maybe using techniques in Bloch: Moving lemma for higher Chow groups, from Spivakovsky's work. The other relating to descriptions of A1-homotopy types: rational case is conjectural, integral case quite unclear.
File: Lectures on motivic cohomology written by Deligne, in Voevodsky folder. Contains discussion of some topics including: some kind of equivariant version, i.e. schemes with action of a finite flat group scheme, and an equivariant analogue of the Nisnevich topology. Notion of solid sheaves, including Thom spaces of VBs. On of the main ideas seem to be the extension of certain functors from schemes to the motivic homotopy category, for example quotienting by a G-action, fixed points, and symmetric products. I think these functors are well-behaved wrt solid sheaves.
Strunk and Herrmann on a model for the motivic homotopy theory: http://front.math.ucdavis.edu/1007.3153
<]]>- Motivic homotopy theory readingWrite comment View comments
This is a list useful reading on homotopy theory in algebraic geometry. For a lot more resources, see the resource page maintained by Aravind Asok
Background in Algebraic Geometry
Summary of background in algebraic geometry: notes by Marc Levine.
Many useful notes, including an introduction to sheaf cohomology, can be found at The Rising Sea
Background in Category Theory
Basic category theory
Additive and abelian categories
Notes by Fesenko.
Triangulated categories
Notes by Henning Krause.
Model categories
A very readable introduction by Dwyer and Spalinski.
Higher categories
A guide by Cheng and Lauda.
Background in Algebraic Topology
The excellent book by May should cover everything.
A nice background paper by Dundas
Some slides by Strickland on stable homotopy
See reading list on page 2 of Strickland's bestiary
Unstable homotopy theory
DEA thesis by Joel Riou.
The original paper by Morel and Voevodsky
Stable homotopy theory
Notes from Tyler Lawson's page
Voevodsky's ICM lecture
Gillet in K-theory handbook, section 2.5.
Many nice things are in these notes by Dundas. More generally, check the Nordfjordeid summer school volume on motivic homotopy theory. Available in folder AG/Motives.
Talk in Toronto by Levine
See lectures of Levine at the Asian-French summer school
Voevodsky: Open problems I
Slides of Jardine
Levine: The homotopy coniveau filtration. (Looks very nice) See also Chow's moving lemma and the homotopy coniveau tower.
Check all other papers of Voevodsky!
Weibel's road map
Hornbostel on motivic chromatic homotopy theory.
Po Hu on the Picard group, and on S-modules in the stable homotopy category of schemes. Here is also something on the Steinberg relation
Check the paper on Motivic functors by Bjørn Ian Dundas, Oliver Röndigs, Paul Arne Østvær.
Motivic cell structures , by Daniel Dugger and Daniel C. Isaksen
Levine slides on Postnikov towers. See by the way everything on Levine's web page, for example this
Biedermann: L-stable functors. "This gives a particularly easy construction of the classical and the motivic stable homotopy category with the correct smash product."
Weight structures, weight filtrations, weight spectral sequences, and weight complexes (for motives and spectra) , by Mikhail V. Bondarko: K0843
Joseph Ayoub thesis, on the six operations formalism in the stable homotopy category. Also: Ayoub in Nagel and Peters: nice exposition of various categories.
Opérations sur la K-théorie algébrique et régulateurs via la théorie homotopique des schémas, by Joël Riou
Half-page intro by Grayson, K-th handbook p 63.
Short intro by Kahn in K-theory handbook, pp374 (a possible starting point for rewriting stuff).
Some abstrast/axiomatic views on stable homotopy
Joel Riou on the stable homotopy category of a site with interval. See also K0825
Interesting mathematicians
Levine Toen Jardine Morel Voevedsky Kahn
Ideas/questions
Can one work with infinite loop space machines in algebraic geometry? Can this lead to a recognition principle?
Some Open questions - a summary from a conference in Palo Alto
<]]>- Motivic integrationWrite comment View comments
Some introductory notes by Blickle. See also Craw and perhaps also Hales. There are also notes by Blickle in folder AG/Motives, maybe the same notes.
http://ncatlab.org/nlab/show/motivic+integration
Craw: An introduction to motivic integration. On arXiv, and in folder AG/Various
arXiv:1004.4260 The yoga of schemic Grothendieck rings, a topos-theoretical approach from arXiv Front: math.KT by Hans Schoutens We propose a suitable substitute for the classical Grothendieck ring of an algebraically closed field, in which any quasi-projective scheme is represented, while maintaining its non-reduced structure. This yields a more subtle invariant, called the schemic Grothendieck ring, in which we can formulate a form of integration resembling Kontsevich's motivic integration via arc schemes. Whereas the original construction was via definability, we have translated in this paper everything into a topos-theoretic framework.
It is possible that motivic integration, or at least the notion of (convergence of) power series over the Grothendieck ring, is related to finiteness conditions on simplicial presheaves/simplicial varieties.
arXiv:0912.4887 A note on motivic integration in mixed characteristic from arXiv Front: math.AG by Johannes Nicaise, Julien Sebag We introduce a quotient of the Grothendieck ring of varieties by identifying classes of universally homeomorphic varieties. We show that the standard realization morphisms factor through this quotient, and we argue that it is the correct value ring for the theory of motivic integration on formal schemes and rigid varieties in mixed characteristic. The present note is an excerpt of a detailed survey paper which will be published in the proceedings of the conference "Motivic integration and its interactions with model theory and non-archimedean geometry" (ICMS, 2008).
arXiv:1006.5475 Invariance of orientation data for ind-constructible Calabi-Yau $A_{\infty}$ categories under derived equivalence from arXiv Front: math.CT by Ben Davison We study orientation data, as introduced by Kontsevich and Soibelman in order to define well-behaved integration maps from the motivic Hall algebra of 3-dimensional Calabi-Yau categories to rings of motives. We start with an example that demonstrates the role of orientation data in this story, before working through the technical details. We give an account of orientation data in the case of categories of compactly supported sheaves on noncompact Calabi-Yau three-folds. We finally study how this structure behaves under pullbacks along quasi-equivalences of categories, prove Kontsevich and Soibelman's conjecture regarding this behaviour, and also some stronger theorems regarding flops and more general tilts.
arXiv:1102.3832 Motivic integration in all residue field characteristics for Henselian discretely valued fields of characteristic zero from arXiv Front: math.AG by R. Cluckers, F. Loeser We extend the formalism and results on motivic integration from ["Constructible motivic functions and motivic integration", Invent. Math., Volume 173, (2008) 23-121] to mixed characteristic discretely valued Henselian fields with bounded ramification. We also generalize the equicharacteristic zero case of loc. cit. by giving, in all residue characteristics, an axiomatic approach (instead of only using Denef-Pas languages) and by using richer angular component maps. In this setting we prove a general change of variables formula and a general Fubini Theorem. Our set-up can be specialized to previously known versions of motivic integration by e.g. the second author and J. Sebag and to classical p-adic integrals.
<]]>- Motivic L-functionWrite comment View comments
On zeros of motivic L-functions. Article by ANDRZEJ DABROWSKI and JACEK POMYKALA. Same authors: Nonvanishing of motivic L-functions
<]]>- Motivic spectral sequenceWrite comment View comments
arXiv:1210.2242 On the motivic spectral sequence fra arXiv Front: math.AG av Grigory Garkusha, Ivan Panin It is shown that the Grayson motivic spectral sequence is isomorphic to the motivic spectral sequence produced by the Voevodsky slice tower for the motivic K-theory spectrum KGL. This solves Suslin's problem for these two spectral sequences in the affirmative. To prove this, one has to solve the Voevodsky problem for slices of KGL. The latter problem was first solved by Levine by using the coniveau tower, but our methods are entirely different from Levine's ones.
<]]>- Motivic stable homotopy theoryWrite comment View comments
Voevodsky's Open problems paper, in Voevodsky folder.
http://mathoverflow.net/questions/27239/relation-between-motivic-homotopy-category-and-the-derived-category-of-motives contains nice answer by SimonPL
arXiv:0907.1510 Periodizable motivic ring spectra. from arXiv Front: math.AG by Markus Spitzweck. We show that the cellular objects in the module category over a motivic E infinity ring spectrum E can be described as the module category over a graded topological spectrum if E is strongly periodizable in our language. A similar statement is proven for triangulated categories of motives. Since MGL is strongly periodizable we obtain topological incarnations of motivic Landweber spectra. Under some categorical assumptions the unit object of the model category for triangulated motives is as well strongly periodizable giving motivic cochains whose module category models integral triangulated categories of Tate motives.
arXiv:1002.2368 Motivic connective K-theories and the cohomology of A(1) from arXiv Front: math.KT by Daniel C. Isaksen, Armira Shkembi We make some computations in stable motivic homotopy theory over Spec \mathbb{C}, completed at 2. Using homotopy fixed points and the algebraic K-theory spectrum, we construct a motivic analogue of the real K-theory spectrum KO. We also establish a theory of connective covers to obtain a motivic version of ko. We establish an Adams spectral sequence for computing motivic ko-homology. The E2-term of this spectral sequence involves Ext groups over the subalgebra A(1) of the motivic Steenrod algebra. We make several explicit computations of these E2-terms in interesting special cases.
See articles by Pelaez, including Functoriality of the slice filtration (arxiv)
arXiv:1206.3645 Noncommutative Motives I: A Universal Characterization of the Motivic Stable Homotopy Theory of Schemes from arXiv Front: math.AG by Marco Robalo Let $\V$ be a symmetric monoidal model category and let $X$ be an object in $\V$. From this we can construct a new symmetric monoidal model category $Sp^{\Sigma}(\V,X)$ of symmetric spectra objects in $\V$ with respect to $X$, together with a left Quillen monoidal map $\V\to Sp^{\Sigma}(\V,X)$ sending $X$ to an invertible object. In this paper we use the recent developments in the subject of Higher Algebra to understand the nature of this construction. Every symmetric monoidal model category has an underlying symmetric monoidal $(\infty,1)$-category and the first notion should be understood as a mere "presentation" of the second. Our main result is the characterization of the underlying symmetric monoidal $\infty$-category of $Sp^{\Sigma}(\V,X)$, by means of a universal property inside the world of symmetric monoidal $(\infty,1)$-categories. In the process we also describe the link between the construction of ordinary spectra and the one of symmetric spectra. As a corollary, we obtain a precise universal characterization for the motivic stable homotopy theory of schemes with its symmetric monoidal structure. This characterization trivializes the problem of finding motivic monoidal realizations and opens the way to compare the motivic theory of schemes with other motivic theories.
<]]>- Motivic t-structureWrite comment View comments
- <]]>
- Moving lemmasWrite comment View comments
Moving lemma for additive Chow groups (Park, Krishna): http://front.math.ucdavis.edu/0909.3155
<]]>- MulticategoryWrite comment View comments
- <]]>
- Multiple zeta valuesWrite comment View comments
arXiv:1101.1594 Multiple Dedekind Zeta Functions from arXiv Front: math.NT by Ivan Horozov In this paper we define multiple Dedekind zeta functions as a new type of iterated integrals. This new class of functions have many properties. They can be written as infinite sums. They have integral representation and meromorphic continuation. We also prove that at the positive integers the multiple Dedekind zeta values are periods. In particular, the Dedekind zeta function can be written in terms of the new type of iterated integral and at the positive integers the corresponding iterated integrals give periods.
arXiv:0911.2643 Multizeta values: Lie algebras and periods on $\mathfrak{M}{0,n}$ from arXiv Front: math.NT by Sarah Carr (there are also other things by Carr) This thesis is a study of algebraic and geometric relations between multizeta values. In chapter 2, we prove a result which gives the dimension of the associated depth-graded pieces of the double shuffle Lie algebra in depths 1 and 2. In chapters 3 and 4, we study geometric relations between multizeta values coming from their expression as periods on $\mathfrak{M}{0,n}$. The key ingredient in this study is the top dimensional de Rham cohomology of special partially compactified moduli spaces associated to multizeta values. In chapter 3, we give an explicit expression for a basis, represented by polygons, of this cohomology. In chapter 4, we generalize this method to explicitly describe the bases of the cohomology of other partially compactified moduli spaces. This thesis concludes with a result which gives a new presentation of $Pic(\overline{\mathfrak{M}}_{0,n})$.
arXiv:0907.2557 The Multiple Zeta Value Data Mine from arXiv Front: math.NT by J. Blümlein, D. J. Broadhurst, J. A. M. Vermaseren We provide a data mine of proven results for multiple zeta values (MZVs) of the form $\zeta(s1,s2,...,sk)=\sum{n1>n2>...>nk>0}^\infty {1/(n1^{s_1}
... nk^{sk})}$ with weight $w=\sum{i=1}^k si$ and depth $k$ and for Euler sums of the form $\sum{n1>n2>...>nk>0}^\infty t{(\epsilon1^{n1} ...\epsilon1 ^{nk})/ (n1^{s1} ... nk^{sk}) }$ with signs $\epsilon_i=\pm1$. Notably, we achieve explicit proven reductions of all MZVs with weights $w\le22$, and all Euler sums with weights $w\le12$, to bases whose dimensions, bigraded by weight and depth, have sizes in precise agreement with the Broadhurst--Kreimer and Broadhurst conjectures. Moreover, we lend further support to these conjectures by studying even greater weights ($w\le30$), using modular arithmetic. To obtain these results we derive a new type of relation for Euler sums, the Generalized Doubling Relations. We elucidate the "pushdown" mechanism, whereby the ornate enumeration of primitive MZVs, by weight and depth, is reconciled with the far simpler enumeration of primitive Euler sums. There is some evidence that this pushdown mechanism finds its origin in doubling relations. We hope that our data mine, obtained by exploiting the unique power of the computer algebra language {\sc form}, will enable the study of many more such consequences of the double-shuffle algebra of MZVs, and their Euler cousins, which are already the subject of keen interest, to practitioners of quantum field theory, and to mathematicians alike.
<]]>- MumfordWrite comment View comments
On the Grothendieck circle it is claimed (Jan 2009) that a volume of Mumford\'s complete works will appear soon, including some letters from Grothendieck.
Selected papers, 1 vol including the word variety in the subtitle
<]]>- MurreWrite comment View comments
Some publications
- Some lectures on Grothendieck's theory of the fundamental group. (Michael has a hard copy)
<]]>- Murre's conjectureWrite comment View comments
Motives volumes, and stuff by Vial.
arXiv:1110.0668 Remarks on Murre's conjecture on Chow groups from arXiv Front: math.AG by Kejian Xu, Ze Xu For certain product varieties, Murre's conjecture on Chow groups is investigated. In particular, it is proved that Murre's conjecture (B) is true for two kinds of four-folds. Precisely, if $C$ is a curve and $X$ is an elliptic modular threefold over $k$ (an algebraically closed field of characteristic 0) or an abelian variety of dimension 3, then Murre's conjecture (B) is true for the fourfold $X\times C.$
<]]>