Glossary

arXiv:0909.1849 Canonical extensions of Néron models of Jacobians from arXiv Front: math.NT by Bryden Cais Let A be the Néron model of an abelian variety AK over the fraction field K of a discrete valuation ring R. Due to work of Mazur-Messing, there is a functorial way to prolong the universal extension of AK by a vector group to a smooth and separated group scheme over R, called the canonical extension of A. In this paper, we study the canonical extension when AK=JK is the Jacobian of a smooth proper and geometrically connected curve XK over K. Assuming that XK admits a proper flat regular model X over R that has generically smooth closed fiber, our main result identifies the identity component of the canonical extension with a certain functor Pic^{\natural,0}{X/R} classifying line bundles on X that have partial degree zero on all components of geometric fibers and are equipped with a regular connection. This result is a natural extension of a theorem of Raynaud, which identifies the identity component of the Néron model J of JK with the functor Pic^0{X/R}. As an application of our result, we prove a comparison isomorphism between two canonical integral structures on the de Rham cohomology of XK.

arXiv:1209.5556 Néron models and base change from arXiv Front: math.AG by Lars Halvard Halle, Johannes Nicaise We study various aspects of the behaviour of Néron models of semi-abelian varieties under finite extensions of the base field, with a special emphasis on wildly ramified Jacobians. In Part 1, we analyze the behaviour of the component groups of the Néron models, and we prove rationality results for a certain generating series encoding their orders. In Part 2, we discuss Chai's base change conductor and Edixhoven's filtration, and their relation to the Artin conductor. All of these results are applied in Part 3 to the study of motivic zeta functions of semi-abelian varieties. Part 4 contains some intriguing open problems and directions for further research. The main tools in this work are non-archimedean uniformization and a detailed analysis of the behaviour of regular models of curves under base change.

<]]>

Neron-Ogg-ShafarevichWrite comment View comments

http://mathoverflow.net/questions/108953/motivic-generalisation-of-neron-ogg-shaferevich-criterion

<]]>

Neron-Severi groupWrite comment View comments

http://mathoverflow.net/questions/79512/non-degenerate-pairing-on-neron-severi-group

arXiv:1210.3720 Computing Néron-Severi groups and cycle class groups fra arXiv Front: math.AG av Bjorn Poonen, Damiano Testa, Ronald van Luijk Assuming the Tate conjecture and the computability of étale cohomology with finite coefficients, we give an algorithm that computes the Néron-Severi group of any smooth projective geometrically integral variety, and also the rank of the group of numerical equivalence classes of codimension p cycles for any p.

<]]>

NerveWrite comment View comments

nLab

http://ncatlab.org/nlab/show/nerve+and+realization

http://mathoverflow.net/questions/68293/nerves-of-simplicial-objects-in-categories-waldhausens-s-construction

http://mathoverflow.net/questions/117401/is-every-functor-inducing-a-homotopy-equivalence-a-composition-of-adjoint-functor claims that any adjoint functor induced homotopy equiv on the nerve

For any (small?) category Mathematical formula , one defines a simplicial set 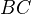, called its nerve. The 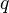-simplices of a category is the set of functors 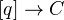, see Dundas, page 24, for details. This construction is an extension of the Yoneda embedding 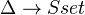, and embeds 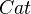as a full subcategory of 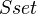. The nerve has a left adjoint.

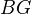If Mathematical formula is given by a group , then is a 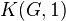space.

Every nerve of a group is a Kan complex, but not every nerve of a category. Actually, a nerve of a small category is a fibrant simplicial set iff the category is a groupoid.

Remark: Every simplicial group (regarded as a simplicial set) is fibrant.

Cox: Homotopy limits and the homotopy type of functor categories; has an alternative description of the nerve of a small category. MR0407022

Ref: Page 10 of Baues: Homotopy types (e)

Nerves for bicats, see http://arxiv.org/abs/0903.5058

Q from Maltsiniotis to ALGTOP: Let $N$ be the nerve functor from categories to simplicial sets and $c$ its left adjoint. It is well known that $c$ (or equivalently $Nc$) is not compatible with weak equivalences, but what about weakly contractible objects? Grothendieck asks in Pursuing Stacks to find a weakly contractible simplicial set $X$ such that $c(X)$ (or $Nc(X)$) is not weakly contractible, or prove that no such $X$ exist.

<]]>

Nevanlinna theoryWrite comment View comments

A course syllabus, with relations to diophantine approximation.

Book by Ru in Diophantine approximation folder

Expository article of Soulé in Asterisque 183 MR1065158

<]]>

Nilpotence conjectureWrite comment View comments

http://mathoverflow.net/questions/40432/identifying-the-stacks-in-devinatz-hopkins-smith

Eric P has three blog posts on Devinatz-Hopkins-Smith. Third one here: http://chromotopy.org/?p=262

<]]>

Nilpotent spaceWrite comment View comments

Probably a good source is Sullivan's MIT notes.

LNM304 (B-K) says on p 7 that nilpotent means that the up to homotopy, the Postnikov tower can be refined to a tower of principal fibrations.

Ref: Jardine-Goerss section VI.6. Nilpotent spaces admit a yoga of crawling up a Postnikov tower.

Hilton et al: Localization of nilpotent groups and spaces (Homotopy th folder)

<]]>

NisnevichWrite comment View comments

Web page

<]]>

Nisnevich topologyWrite comment View comments

Nisnevich: The completely decomposed topology on schemes and associated descent spectral sequences in algebraic K-theory

May useful things in Morel-Voevodsky: A1-homotopy theory of schemes, see for example start of chapter 3 for a list of useful properties comparing it to Zariski and etale. Section 3.2.3 contains results on "gluing, homotopy purity, and the blowup square" which require the topology to be (at least as strong as?) the Nisnevich top.

Voevodsky's Nordfjordeid lecture - supernice (Voevodsky folder). Has a serious appendix on the Nisnevich topology, Nisnevich descent, and model structures.

http://mathoverflow.net/questions/78431/nisnevich-topology-on-non-locally-noetherian-schemes

Memo notes from Jardine: Generalized etale... pp 282

Let Mathematical formula be a locally Noetherian scheme. The Nisnevich site (or cd-site, completely decomposed site) of are defined as follows. Objects are separated etale morphisms 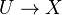of finite type (i.e. as in the separated etale site). Morphisms are -scheme morphisms. A collection 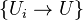of morphisms is a covering family if for every point 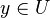Mathematical formula , the map 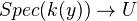lifts to some .

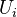If 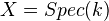Mathematical formula for a field , then the above objects are finite disjoint unions of Spec of finite separable extensions of . A family 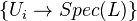is a covering family iff at least one of the 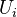has a component equal to 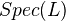. Hence there is only one covering sieve for each finite separable extension 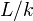, and the sheaf condition is simply that of "additivity" for disjoint unions of fields. More details on the case of a field.

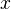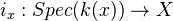For Mathematical formula a point of , have the morphism . Composition with the induced functor 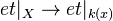defines a direct image functor 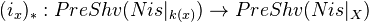which preserves sheaves. It has a left adjoint 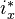defined by left Kan extension. Some consequences of this.

If a presheaf Mathematical formula on 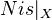is the restriction of a contravariant functor defined on a sufficiently large category of schemes, and if is continuous, then there is an isomorphism .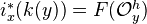

Lemma: Suppose that Mathematical formula is an additive presheaf on 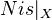. Then 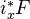is an additive presheaf on 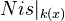. (Additive means: taking disjoint unions to products). Also, if is a sheaf, so is .

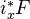The above gives us two different points of view on stalks in the Nisnevich topology. Spelling out of these things, and conditions for maps of sheaves to be IMs (skipped here). In many cases, maps of presheaves arise from natural transformations which are continuous and "globally defined". Then the induced map of associated sheaves is an isomorphism "iff it is so on henselizations of local rings". Example: Presheaves of stable homotopy groups arising from K-theory presheaves of spectra.

Def: Nisnevich excision property, for a presheaf of spectra on the Nisnevich site of a scheme. This condition says that (1) 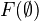Mathematical formula is contractible and (2) For each map 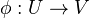in 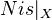and a closed subscheme 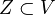such that 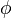induces an isomorphism 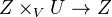, the obvious commutative diagram of spectra involving 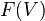, , 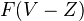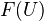and 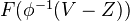is homotopy cartesian.

Examples: If a Noetherian scheme is a also separated and regular, then the K-theory presheaf of spectra on the Nisnevich site has this property (need hyps to invoke Quillen's localization thm). Smashing with a constant presheaf of spectra preserves the Nisnevich excision property. The Nisnevich excision property is stable under pointwise stable equivalence.

Lemma: Roughly: Given a presheaf Mathematical formula of spectra satisfying Nis excision, there is a pointwise weak equivalence from this presheaf to a presheaf 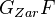for which "open subset inclusions induces stable fibrations".

Let Mathematical formula be as in the lemma. Then satisfies Zariski excision, so is additive up to stable equivalence, meaning that the corresponding presheaves of stable homotopy groups are additive.

For a closed subset 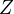Mathematical formula of 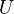, where 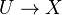is in 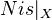, we define a presheaf 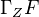as the fibre of 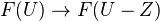. Various properties and applications of this (several pages).

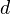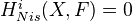Thm (Kato-Saito): Let Mathematical formula be a Noetherian scheme of Krull dimension , and let be a sheaf of abelian groups on the Nisnevich site of . Then for .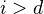

Thms of this kind "forces descent spectral sequences to converge".

An important idea in the above seems to be to prove that under suitable hyps, any choice of globally fibrant model is a pointwise stable equivalence. Actually, this seems to be true in general for Mathematical formula of finite Krull dimension and satisfying Nisnevich excision. This is the Nisnevich descent theorem, essentially, and can also be formulated in terms of a "Godement resolution" for . Details on this, including a construction . A theorem saying that this is a pointwise stable equivalence, under some hyps.

Corollary: Roughly: Smash the K-theory presheaf with a constant presheaf. A globally fibrant model for this for the Nisnevich topology is a pointwise stable equivalence.

<]]>

nLabWrite comment View comments

http://ncatlab.org/nlab/show/mathematics this entry contains some attempt at organising

<]]>

NoetherWrite comment View comments

Collected papers, 1 volume

<]]>

Nonabelian algebraic topologyWrite comment View comments

nLab

<]]>

Nonabelian arithmetic geometryWrite comment View comments

Many video lectures from the Newton institute programme 2009, link including Breuuil, Kakde, Kim, Schneider, Coates, and much more

<]]>

Nonabelian Hodge theoryWrite comment View comments

Toen, Katzarkov, Pantev: Schematic homotopy types and nonabelian Hodge theory. File Toen web publ nht.pdf. Constructs a "Hodge decomposition" (a certain action) on the schematic homotopy type of a smooth projective complex variety. This recovers many other Hodge invariants, short review of these.

C. Simpson. Algebraic aspects of higher nonabelian Hodge theory, math.Algebraic Geometry/9902067.

Chapter 7 of Amoros et al in Complex manifolds folder

Grojnowski essay topic

References The abelian Hodge theorem and its consequences are nicely explained in the textbook of Griffiths and Harris, but also look at the beautiful papers of Deligne: [1] P. Deligne, Travaux de Griffiths, Seminar Bourbaki 376, Lecture Notes in Math 180, Springer Verlag 1970, 213–237 [2] P. Deligne, Theorie des Hodges II, III. Inst. Hautes tudes Sci. Publ. Math. No. 40 (1971), 5–57; Inst. Hautes tudes Sci. Publ. Math. No. 44 (1974), 5–77. and for the non-abelian, some references are: [3] C. Simpson, Nonabelian Hodge theory. Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), [4] C Simpson, Higgs bundles and local systems. Inst. Hautes Etudes Sci. Publ. Math. No. 75 (1992), 5–95. [5] C. Simpson, Moduli of representations of the fundamental group of a smooth projective variety. I,II, Publ. IHES. [6] N. Hitchin, The self-duality equations on a Riemann surface. Proc. London Math. Soc. (3) 55 (1987), no. 1, 59–126.

<]]>

Noncommutative Arakelov theoryWrite comment View comments

arXiv:0911.2479 Arakelov theory of noncommutative arithmetic curves from arXiv Front: math.NT by Thomas Borek The purpose of this article is to initiate Arakelov theory in a noncommutative setting. More precisely, we are concerned with Arakelov theory of noncommutative arithmetic curves. Our first main result is an arithmetic Riemann-Roch formula in this setup. We proceed with introducing the Grothendieck group of arithmetic vector bundles on a noncommutative arithmetic curve and show that there is a uniquely determined degree map, which we then use to define a height function. We prove a duality theorem for this height.

<]]>

Noncommutative geometryWrite comment View comments

[CDATA[http://mathoverflow.net/questions/10512/theories-of-noncommutative-geometry

http://www.ncatlab.org/nlab/show/Kapranov%27s+noncommutative+geometry

http://mathoverflow.net/questions/15327/what-properties-should-spectrum-of-noncommutative-ring-have

A book by Connes and Marcolli: Noncommutative geometry, quantum fields and motives.

http://www.neverendingbooks.org/index.php/langlands-versus-connes.html

http://mathoverflow.net/questions/54186/reference-learning-noncommutative-geometry-and-c-algebras

Connes: Noncommutative geometry (1994). (Book)

Could check arxiv preprints of Michel Van den Bergh

nlab: spectral triple

http://www.noncommutative.org/index.php/top-10-noncommutative-geometry-books-for-newbies/

arXiv:1109.6688 Sklyanin algebras revisited from arXiv Front: math.AG by Igor Nikolaev It is proved that the Sklyanin algebra on 4 generators and 6 relations modulo an ideal is isomorphic to a dense sub-algebra of the noncommutative torus. As a corollary one gets a functor between the categories of elliptic curves and noncommutative tori.

This could be of some interest.

A survey by Mahanta

Lectures of Ginzburg

See arXiv articles by Manin. Survey article by Connes?

Authors to explore when time: Connes, Kontsevich, Feigin, Tsygan

Book: Surveys in noncommutative geometry

Lapidus: In search of the Riemann zeros

Artin and Zhang: Noncommutative projective schemes (1994)

nlab on noncomm geom

nLab on noncommutative algebraic geometry, see also NAG canon, noncomm scheme, descent in NAG.

http://ncatlab.org/nlab/show/spectrum+of+an+abelian+category

http://nlab.mathforge.org/nlab/show/Gabriel-Rosenberg+theorem

nlab on derived noncomm geom

nlab on the work of Maszczyk

http://nlab.mathforge.org/nlab/show/operator+algebra

http://ncatlab.org/nlab/show/locally+affine+space mentions noncommutative smooth spaces

Relevant blogs?

Cortinas has some papers on various forms of cohomology for noncommutative schemes (I think in the sense of Kapranov). All his papers seem to be on the arXiv

<]]>

Noncommutative geometry IIWrite comment View comments

C*-algebras: See many things in the folder Noncomm geom and Cstar-alg. Same for Noncomm geom in the sense of Connes, Cyclic homology

Loday: Cyclic homology. In Noncomm geom folder. Covers many aspects of Cyclic and Hochschild homology. Among many other topics: Secondary char classes (section 11.5), Homology of small categories (App C), periodic and negative cyclic homology, Andre-Quillen homology, Deligne cohomology. For the latter, the main point is that there a cyclic homology complex of Connes which computes integral coeffs reduced Deligne cohomology but which has strictly commutative products!! This is stated for smooth algebras over C, not sure if it can be generalized to more general schemes. Also I am not sure if this has any relevance for non-reduced Deligne cohomology.

<]]>

Noncommutative homotopy theoryWrite comment View comments

Mahanta: http://front.math.ucdavis.edu/0906.5400

Axioms related to Kontsevich-Rosenberg

<]]>

Noncommutative L-functionsWrite comment View comments

arXiv:0908.2928 Noncommutative L-functions for varieties over finite fields from arXiv Front: math.NT by Malte Witte In this article we prove a Grothendieck trace formula for L-functions of not necessarily commutative adic sheaves.

<]]>

Nonunital ringsWrite comment View comments

http://qchu.wordpress.com/2012/11/04/non-unital-rings/

Even more interesting: Nonunital ring spectra.

<]]>

NoriWrite comment View comments

MathSciNet

arXiv

Some publications

A modified Hodge conjecture. Text of a lecture given at Duke, University, March 2003.

<]]>

Normal functionsWrite comment View comments

Can be used for studying algebraic cycles.

Charles: On the zero locus of normal functions and the étale Abel-Jacobi map. http://arxiv.org/abs/0902.1948

arXiv:0910.0628 On the algebraicity of the zero locus of an admissible normal function from arXiv Front: math.AG by Patrick Brosnan, Gregory Pearlstein We show that the zero locus of an admissible normal function on a smooth complex algebraic variety is algebraic.

<]]>

Novikov conjectureWrite comment View comments

Ref: Ferry, Ranicki, Rosenberg: A history and survey of the Novikov conjecture. In some CUP volume, 1995.

Some kind of introduction is in Rosenberg

Here is a survey

Some aspects are discussed by Carlsson in K-theory handbook.

See K0013, K0049

<]]>

Number fieldWrite comment View comments

Bordeaux number fields database: ftp://megrez.math.u-bordeaux.fr/pub/numberfields/

<]]>