Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- p-adic analysisWrite comment View comments
arXiv:0909.4509 Lectures on Non-Archimedean Function Theory from arXiv Front: math.NT by William Cherry Lecture 1 discusses non-Archimedean analogs of classical complex function theory based on the Schnirelman integral. Lecture 2 discusses valuation (Newton) polygons and their consequences and presents a non-Archimedean analog of the Poisson-Jensen formula. Lecture 3 introduces non-Archimedean value distribution theory. Lecture 4 presents an introduction to Benedetto's non-Archimedean analogs of the Ahlfors Island theorems.
<]]>- p-adic differential equationsWrite comment View comments
Authors: Kedlaya, Dwork, Yves Andre
<]]>- p-adic geometric LanglandsWrite comment View comments
Alex Paulin talk abstract: The (de Rham) geometric Langlands correspondence for GL(n) asserts that to an irreducible rank n integrable connection on a complex smooth projective curve X, we may naturally associate a D-module on Bunn(X), the moduli stack of rank n vector bundles on X. Making appropriate changes to the formulation there are also Betti and l-adic versions of the above correspondence. In this talk we consider the rigid (and ultimately motivic) side of the story. In particular we conjecture the existence of a p-adic geometric Langlands correspondence relating rank n F-isocrystals on X (now a curve over Fp) to arithmetic D-modules on Bun_n(X). We will also explore the potential of a motivic version of the GLC which should specialize to each of the above correspondences under appropriate realisations. We will assume no specific background in the geometric Langlands correspondence.
<]]>- p-adic L-functionWrite comment View comments
Review of Faltings: The determinant of cohomology in the etale topology. Theta functions can be viewed as the canonical section of the determinant of cohomology. The corresponding notion in the etale topology would be L-series. "All known constructions of p-adic L-functions seem to be related to some situation where some etale cohomology has vanishing Euler char.
p-adic regulator and p-adic L-functions intro in Washington, in cyclotomic folder
p-adic L-functions: lectures of Kato, and of Iwasawa, in Iwasawa theory folder
[arXiv:1207.2289] On special zeros of $p$-adic $L$-functions of Hilbert modular forms fra arXiv Front: math.NT av Michael Spiess Let $E$ be a modular elliptic curve over a totally real number field $F$. We prove the weak exceptional zero conjecture which links a (higher) derivative of the $p$-adic $L$-function attached to $E$ to certain $p$-adic periods attached to the corresponding Hilbert modular form at the places above $p$ where $E$ has split multiplicative reduction. Under some mild restrictions on $p$ and the conductor of $E$ we deduce the exceptional zero conjecture in the strong form (i.e.\ where the automorphic $p$-adic periods are replaced by the $\cL$-invariants of $E$ defined in terms of Tate periods) from a special case proved earlier by Mok. Crucial for our method is a new construction of the
$p$-adic $L$-function of $E$ in terms of local data.
MR591682 (82c:12014) 12B40 Koblitz, Neal Fp-adic analysis: a short course on recentwork. LondonMathematical Society Lecture Note Series, 46. Cambridge University Press, Cambridge-New York, 1980. 163 pp. $14.95. ISBN 0-521-28060-5 This book gives a nice survey of some recent work on p-adic analysis and p-adic L-functions. The first chapter sketches, usually without proofs, the basics of p-adic analysis, including Newton polygons and p-adic functions. In this and later chapters it is noted how “correcting by Frobenius” extends the domain of many p-adic functions. In the second chapter, the author introduces p-adic measures, including a useful replacement for the nonexistent translation-invariant measure. He constructs the Kubota-Leopoldt p-adic L-functions and evaluates them at 1. He then defines the p-adic gamma function and expresses the derivative of the p-adic L-function at 0 in terms of the p-adic log gamma function (a result due to B. Ferrero and R. Greenberg). The proof, using twisted log gamma functions, is the same as that in a paper of the author [Duke Math. J. 46 (1979), no. 2, 455–468; MR0534062 (80f:12011)]. However, the relation also follows trivially from the easily proved formula of the reviewer MR0406982 expressing the p-adic L-functions in terms of the p-adic log gamma function [see S. Lang, Cyclotomic fields, II, Springer, New York, 1980; MR0566952 (81i:12004)]. In the third chapter the author first treats Gauss and Jacobi sums, L-series for algebraic varieties over finite fields, and Fermat and Artin-Schreier curves and their cohomology. He then proves the Gross-Koblitz formula [B. H. Gross and N. Koblitz, Ann. of Math. (2) 109 (1979), no. 3, 569–581; MR0534763 (80g:12015)], relating Gauss sums and the p-adic gamma function. Stickelberger’s theorem on the factorization of Gauss sums follows as a corollary (Stickelberger’s name is uniformly misspelled). The proof of the Gross-Koblitz formula is similar to the proof given by Lang [op. cit.]; however, the present exposition asks the reader to believe certain cohomological facts, while Lang’s book uses the Dwork trace formula to obtain the Gauss sums, hence is self-contained. The fourth chapter discusses the p-adic regulators of Leopoldt and of Gross. It is proved that Leopoldt’s regulator does not vanish for abelian extensions of Q, and Gross’s conjectures on the behavior of p-adic L-functions at 0 are discussed. The book concludes with an appendix which treats the ˇ Snirel0man integral and the p-adic Stieltjes transform, the Viˇsik transform (the inverse of the Stieltjes transform), and the p-adic spectral theorem.
Good article: MR1327803 (96e:11062) Perrin-Riou, Bernadette(F-PARIS11) Fonctions $L$ $p$-adiques des représentations $p$-adiques. (French. English, French summary) [$p$-adic $L$-functions of $p$-adic representations] Astérisque No. 229 (1995), 198 pp.
MR2096804 (2005h:11135) Bars, Francesc(E-BARA) A relation between $p$-adic $L$-functions and the Tamagawa number conjecture for Hecke characters.
MR2111647 (2005i:11080) Colmez, Pierre La conjecture de Birch et Swinnerton-Dyer $p$-adique (Looks like an excellent survey)
http://mathoverflow.net/questions/10603/does-p-adic-l-function-determine-the-l-function
http://mathoverflow.net/questions/13287/special-values-of-p-adic-l-functions
Soulé on cyclotomic units in Asterisque 147-148 MR891430, seems to be a really nice paper, on groups of cyclotomic units in odd K-groups of rings of integers, and relation to p-adic regulators and p-adic L-functions.
<]]>- p-adic regulatorWrite comment View comments
Choo and Snaith compares various constructions. Looks good. Good refs.
The p-adic regulator of Huber and Kings.
See maybe also Kanetomo Sato on arxiv and elsewhere.
Georg Tamme on various comparison results: http://front.math.ucdavis.edu/1111.4109
arXiv:1004.1357 Characteristic classes for p-adic étale Tate twists and the image of p-adic regulators from arXiv Front: math.KT by Kanetomo Sato In this paper, we construct Chern class maps and cycle class maps with values in p-adic étale Tate twists [S2]. We also relate the p-adic étale Tate twists with the finite part of Bloch-Kato. As an application, we prove that the integral part of p-adic regulator maps has values in the finite part of Galois cohomology under certain assumptions.
Check arxiv preprints of Ambrus Pal for rigid analytic regulator on K2 and special values.
Check arxiv and other places for de Jeu and Besser, for syntomic regulators.
MR0891420 (88h:11077) Federer, Leslie Jane(1-OKS) The nonvanishing of Gross' $p$-adic regulator Galois cohomologically. Journées arithmétiques de Besançon (Besançon, 1985). Astérisque No. 147-148 (1987), 71--77, 343.
MR1427624 (98a:14031) Niziol, Wieslawa(1-CHI) On the image of $p$-adic regulators. Invent. Math. 127 (1997), no. 2, 375--400.
MR2231958 (2007d:19007) Asakura, Masanori(J-KYUSGM) Surjectivity of $p$-adic regulators on $K\sb 2$ of Tate curves.
<]]>- p-compact groupsWrite comment View comments
See Dwyer: Lie groups and p-compact groups, ICM1998
<]]>- p-curvature conjectureWrite comment View comments
Kisin
Andr´e,Yves [Andr´e, Yves1] (F-ENS-DAM) Sur la conjecture des p-courbures de Grothendieck-Katz et un probl`eme deDwork. (French. French summary) [The Grothendieck-Katz p-curvature conjecture and a problem of Dwork] Geometric aspects of Dwork theory.Vol. I, II, 55–112, Walter de Gruyter GmbH & Co.KG, Berlin, 2004.
A. Chambert-Loir [Ast´erisque No. 282 (2002), Exp. No. 886, viii, 175–209; MR1975179 (2004f:11062)].
<]]>- p-divisible groupsWrite comment View comments
M. Rapoport et T. Zink, Period spaces for p-divisible groups, Annals of Mathematics Studies, Volume 141
See pdivbook in Galois rep folder
See seminar program in ALG GEOM/Various/p-divsble...
<]]>- p-local homotopy typeWrite comment View comments
Sullivan's MIT notes (Homotopy folder). Excellent stuff on localizations, completions, profinite, p-local and rational homotopy types. p-adic homotopy theory. Relation to etale homotopy theory! Remark: The Sullivan conjecture is about the contractibility of the space of maps from the classifying space of a finite group to a finite-dimensional CW complex.
<]]>- ParkWrite comment View comments
- <]]>
- Parshin theoryWrite comment View comments
Related: Higher-dimensional local fields and higher-dimensional adeles. See arxiv introduction by Morrow, and other papers by him and the Fesenko school.
Aka Parshin-Kato theory.
Kato ICM 1990: Generalized class field theory.
arXiv:1204.4520 Higher adeles and non-abelian Riemann-Roch from arXiv Front: math.KT by T. Chinburg, G. Pappas, M. J. Taylor We show a Riemann-Roch theorem for group ring bundles over an arithmetic surface; this is expressed using the higher adeles of Beilinson-Parshin and the tame symbol via a theory of adelic equivariant Chow groups and Chern classes. The theorem is obtained by combining a group ring coefficient version of the local Riemann-Roch formula as in Kapranov-Vasserot with results on K-groups of group rings and an explicit description of group ring bundles over P^1. Our set-up provides an extension of several aspects of the classical Fr"ohlich theory of the Galois module structure of rings of integers of number fields to arithmetic surfaces.
Functional analysis on the eve of the 21st century Contains article by Kapranov: Analogies between the Langlands Correspondence and Topological QFT. Follow-up here at MO.
arXiv:1002.2698 A refinement of the Parshin symbol for surfaces from arXiv Front: math.AG by Ivan Horozov On an algebraic curve there are Tate symbols, which satisfy Weil reciprocity law. The analogues in higher dimensions are the Parshin symbols, which satisfy Kato-Parshin reciprocity laws. We give a refinement of the Parshin symbol for surfaces, using iterated integrals in the sense of Chen. The product of the refined symbol over the cyclic permutations of the functions recovers the Parshin symbol. Also, we construct a logarithmic version of the Parshin symbol. We prove reciprocity laws for both the refined symbol and a logarithm of the Parshin symbol.
arXiv:1006.4721 Formal completion of a category along a subcategory from arXiv Front: math.CT by Alexander I. Efimov Following an idea of Kontsevich, we introduce and study the notion of formal completion of a compactly generated (by a set of objects) enhanced triangulated category along a full thick essentially small triangulated subcategory.
In particular, we prove (answering a question of Kontsevich) that using categorical formal completion, one can obtain ordinary formal completions of Noetherian schemes along closed subschemes. Moreover, we show that Beilinson-Parshin adeles can be also obtained using categorical formal completion.<]]>- Path objectWrite comment View comments
In a model category, a path object for an object
 is a factorisation of the diagonal map
is a factorisation of the diagonal map 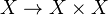 into a WE followed by a fibration.
into a WE followed by a fibration.A path object is the dual of a cylinder object.
The functorial factorisations provide a functorial path object, denoted by
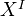 .
.In situations where the category is not ("yet") a model category, one knows that path objects exist whenever the category is a simplicial category.
<]]>- PDF editorsWrite comment View comments
http://www.nitropdf.com/free/hammer/index.htm online free tool
See also the thread at giga: http://gigapedia.com/threads/3864
<]]>- Perfect complexWrite comment View comments
arXiv:1210.2827 Proper local complete intersection morphisms preserve perfect complexes fra arXiv Front: math.AG av B. Toën Let $f : X \longrightarrow Y$ be a proper and local complete intersection morphism of schemes. We prove that $\mathbb{R}f_{*}$ preserves perfect complexes, without any projectivity or noetherian assumptions. This provides a different proof of a theorem by Neeman and Lipman based on techniques from derived algebraic geometry to proceed a reduction to the noetherian case.
<]]>- Perfectoid spacesWrite comment View comments
See all by Scholze, on his webpage, on MO, and on arXiv
<]]>- PeriodsWrite comment View comments
arXiv:1102.2273 Degrees of periods from arXiv Front: math.NT by Jianming Wan We introduce the concept of degree to classify the periods in the sense of Kontsevich. Using this notion we give some new understanding of some problems in transcendental number theory.
http://ncatlab.org/nlab/show/period
http://mathoverflow.net/questions/99791/on-grothendiecks-period-relations
<]]>- PermutationsWrite comment View comments
- <]]>
- Perverse sheavesWrite comment View comments
Gelfand-Manin: Algebra V
BBD
Dimca: Sheaves in topology. In Homol alg folder
http://www.ncatlab.org/nlab/show/perverse+sheaf
arXiv:1004.2983 What is a perverse sheaf? from arXiv Front: math.AG by Mark Andrea de Cataldo, Luca Migliorini Three-page article on the notion of perverse sheaf to appear in the "What is?" series in the Notices of the AMS.
http://mathoverflow.net/questions/74116/crystalline-analogue-of-perverse-sheaves
Kiehl and Weissauer: Weil conj, perverse sheaves, etc
For some notes on perverse sheaves and vanishing cycles, see folder AG/Perverse sheaves.
http://mathoverflow.net/questions/55790/bad-behaviour-of-perverse-sheaves-over-general-bases
arXiv:1002.1686 Notes on Beilinson's "How to glue perverse sheaves" from arXiv Front: math.CT by Ryan Reich The titular, foundational work of Beilinson not only gives a technique for gluing perverse sheaves but also implicitly contains constructions of the nearby and vanishing cycles functors of perverse sheaves. These constructions are completely elementary and show that these functors preserve perversity and respect Verdier duality on perverse sheaves. The work also defines a new, "maximal extension" functor, which is left mysterious aside from its role in the gluing theorem. In these notes, we present the complete details of all of these constructions and theorems.
math/0005152 Perverse coherent sheaves (after Deligne) from arXiv Front: math.AG by Roman Bezrukavnikov This note is mostly an exposition of an unpublished result of Deligne, which introduces an analogue of perverse $t$-structure on the derived category of coherent sheaves on a Noetherian scheme with a dualizing complex. Construction extends to the category of coherent sheaves equivariant under an action of an algebraic group; though proof of the general statement in this case does not require new ideas, it provides examples (such as sheaves on the nilpotent cone of a semi-simple group equivariant under the adjoint action) where construction of coherent "intersection cohomology" sheaves works.
math/9908107 Notes on Perverse Sheaves and Vanishing Cycles from arXiv Front: math.AG by David B. Massey 1 person liked this A working mathematician's summary of many results on the derived category, perverse sheaves, and vanishing cycles. This is the February 2010 version.
<]]>- PhysicsWrite comment View comments
See all books in my PHYSICS folder
See also Quantum stuff, under ALGEBRA
nLab on physics
Les relations entre les mathématiques et la physique théorique, 23--42, Inst. Hautes Études Sci., Bures-sur-Yvette, 1998. This volume might be not officially published.
Robin Ticciati, Quantum Field Theory for Mathematicians, Cambridge University Press, Cambridge, 1999
Enumerative Geometry and String Theory (Sheldon Katz?)
<]]>- Physics and number theoryWrite comment View comments
There is a new journal on these subjects.
A strange resource page of Watkins
N Th and Physics folder, probably under Number Th
arXiv:1003.2986 On Fields over Fields from arXiv Front: math.AG by Yang-Hui He We investigate certain arithmetic properties of field theories. In particular, we study the vacuum structure of supersymmetric gauge theories as algebraic varieties over number fields of finite characteristic. Parallel to the Plethystic Programme of counting the spectrum of operators from the syzygies of the complex geometry, we construct, based on the zeros of the vacuum moduli space over finite fields, the local and global Hasse-Weil zeta functions, as well as develop the associated Dirichlet expansions. We find curious dualities wherein the geometrical properties and asymptotic behaviour of one gauge theory is governed by the number theoretic nature of another.
arXiv:0906.1065 Archimedean L-factors and Topological Field Theories I from arXiv Front: math.AG by Anton Gerasimov, Dimitri Lebedev, Sergey Oblezin We propose a functional integral representation for Archimedean L-factors given by products of Gamma-functions. The corresponding functional integral arises in the description of type A equivariant topological linear sigma model on a disk. The functional integral representation provides in particular an interpretation of the Gamma-function as an equivariant symplectic volume of an infinite-dimensional space of holomorphic maps of the disk to C. This should be considered as a mirror-dual to the classical Euler integral representation of the Gamma-function. We give an analogous functional integral representation of q-deformed Gamma-functions using a three-dimensional equivariant topological linear sigma model on a handlebody. In general, upon proper ultra-violent completion, the topological sigma model considered on a particular class of three-dimensional spaces with a compact Kahler target space provides a quantum field theory description of a K-theory version of Gromov-Witten invariants.
<]]>- PicardWrite comment View comments
Oeuvres, 4 volumes
<]]>- Picard categoriesWrite comment View comments
- <]]>
- Picard groupWrite comment View comments
http://mathoverflow.net/questions/52135/picard-group-of-scheme-over-dvr
Title: On the Picard number of K3 surfaces over number fields Authors: François Charles http://front.math.ucdavis.edu/1111.4117 Abstract: We discuss some aspects of the behavior of specialization at a finite place of Néron-Severi groups of K3 surfaces over number fields. We give optimal lower bounds for the Picard number of such specializations, thus answering a question of Elsenhans and Jahnel. As a consequence of these results, we show that it is possible to explicitly compute the Picard number of any given K3 surface over a number field.
<]]>- Picard schemeWrite comment View comments
LNM174 Iversen: Includes stuff on Pic scheme of a family of curves.
http://mathoverflow.net/questions/33814/picard-groups-of-non-projective-varieties
<]]>- PirashviliWrite comment View comments
- <]]>
- PL categoryWrite comment View comments
The category of piecewise linear spaces. See Rourke and Sanderson. Also: K0012
Julian mentioned something about using PL forms on a simplicial set model of a space, as a replacement for the de Rham cochains, in case the space does not have a smooth structure, in connection with rational homotopy theory.
<]]>- PoincareWrite comment View comments
Oeuvres, at least 11 volumes. I think these are available online somewhere. Also at least 2 correspondence volumes, and one Scientific opportunism
<]]>- Poincare dualityWrite comment View comments
Panin and Yagunov on a form of Poincaré duality for theories represented by a T-spectrum.
Alex Shannon mentioned some kind of very general notion of Poincaré duality I think, maybe involving infty-cats.
The Beilinson conjectures should maybe be thought of as a kind of PD (over F1???).
http://mathoverflow.net/questions/9457/do-chains-and-cochains-know-the-same-thing-about-the-manifold
Can Langlands duality be thought of as Poincaré duality in some sense? Both types of duality are reflected in functional equations.
Notes from the Heidelberg-Strasbourg seminar 1966/1967, in Friedman scans folder. Contains for example notes from an exposé of Verdier.
<]]>- Pointed categoryWrite comment View comments
A category (e.g. a model category) is pointed if the morphism from the initial to the terminal object is an isomorphism.
For any model category
 , the corresponding category under the terminal object is a pointed model category
, the corresponding category under the terminal object is a pointed model category 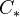 , and there is a faithful, but not full, embedding
, and there is a faithful, but not full, embedding 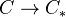 .
.One could also consider similar constructions of model structures on the category under (or over) any object
 .<]]>
.<]]>- Pointed model categoryWrite comment View comments
The homotopy category of a pointed MC is a closed
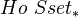 -module. However, it also has additional structure. This is the subject of Hovey, chapter 6. In particular:
-module. However, it also has additional structure. This is the subject of Hovey, chapter 6. In particular:- Can define suspension functor
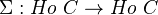
- and its right adjoint, the loop functor
The iterated suspension functor
 lifts to a functor to the category of (abelian) cogroups in
lifts to a functor to the category of (abelian) cogroups in  if
if  (
( ). Same for
). Same for  and the category of groups. (Recall that a group object represents a contravariant functor to Grp, and a cogroup object represents a covariant such functor.)
and the category of groups. (Recall that a group object represents a contravariant functor to Grp, and a cogroup object represents a covariant such functor.)Section 6.2: There is a natural coaction in
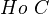 of the cogroup
of the cogroup 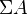 on the cofiber of a cofibration of cofibrant objects
on the cofiber of a cofibration of cofibrant objects 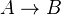 . Also something about an action of the group object
. Also something about an action of the group object 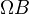 on some fiber. Cofiber sequences and fiber sequences.<]]>
on some fiber. Cofiber sequences and fiber sequences.<]]>- Can define suspension functor
- Pointed simplicial setWrite comment View comments
See also Simplicial set.
A pointed simplicial set is a simplicial object in the category of pointed sets. For these, we can define wedge and smash product; smash is distributive over wedge.
The free/forget adjoint pair between Ab and Set factors through
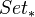 because abelian groups are pointed at zero. The relevant functor from
because abelian groups are pointed at zero. The relevant functor from 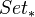 to
to 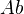 is
is 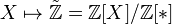 . This functor send wedges to direct sums, and smash products to tensor products, and a "subspace sequence" to an exact sequence. It also takes the n-sphere to the n-th integral Eilenberg-MacLane space.
. This functor send wedges to direct sums, and smash products to tensor products, and a "subspace sequence" to an exact sequence. It also takes the n-sphere to the n-th integral Eilenberg-MacLane space.We have mapping spaces, defined by
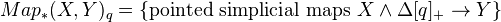
Just as for simplicial sets,
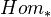 is the 0 simplices of
is the 0 simplices of 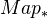 , and we have a "composition" and an exponential adjunction with the smash product.
, and we have a "composition" and an exponential adjunction with the smash product.The loop space of a pointed simplicial set is defined by taking geometric realization, applying the topological loop space functor, and then applying
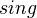 .
.The n-th (reduced, integral) cohomology group of a simplicial set
 is defined as
is defined as 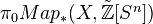
Quote: "A simplicial abelian group is fibrant, so need not apply
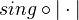 "<]]>
"<]]>- Poisson manifoldWrite comment View comments
- <]]>
- Poitou-Tate dualityWrite comment View comments
arXiv:1104.1484 Poitou-Tate duality over extensions of global fields from arXiv Front: math.NT by Meng Fai Lim In this paper, we formulate and prove a derived category version of Poitou-Tate duality on Galois cohomology of compact modules (with a continuous Galois action) over a pro-p ring, where p is a prime.
<]]>- PolylogarithmWrite comment View comments
See the Motives volumes, especially the first 4 articles in volume 2.
Oberwolfach reports 1 (2004) no 4, on Polylogarithms
Lewin: Structural properties of polylogaritms (book). Also other book by same author??
See Goncharov in K-theory handbook.
K0261: Classical motivic polylogarithm according to Beilinson and Deligne.
Hanamura and MacPherson: Geometric construction of polylogarithms, I and II (1993 and 1996)
Abstracts from a workshop are here
Don Zagier, Polylogarithms, Dedekind zeta functions and the algebraic $K$-theory of fields
Here is a sample article. Another one, and something by Goncharov
MR1290822 (95i:81224) Kirillov, A. N.(4-CAMB-NI) Dilogarithm identities, partitions, and spectra in conformal field theory. (English summary) Algebra i Analiz 6 (1994), no. 2, 152--175; translation in St. Petersburg Math. J. 6 (1995), no. 2, 327--348
MR1312980 (96b:19007) Goncharov, A. B.(1-MIT) Chow polylogarithms and regulators. Math. Res. Lett. 2 (1995), no. 1, 95--112.
MR1348706 (96g:19005) Goncharov, A. B.(1-MIT) Geometry of configurations, polylogarithms, and motivic cohomology. Adv. Math. 114 (1995), no. 2, 197--318.
Nice survey: MR1354171 (97a:19005) Borel, Armand(1-IASP) Values of zeta-functions at integers, cohomology and polylogarithms. Current trends in mathematics and physics, 1--44, Narosa, New Delhi, 1995.
MR1385924 (97h:19009) Gangl, Herbert(D-BONN-MN) Funktionalgleichungen von Polylogarithmen. (German) [Functional equations of polylogarithms]
MR1443532 (98d:11073) Wildeshaus, Jörg(D-MUNS) On an elliptic analogue of Zagier's conjecture. Duke Math. J. 87 (1997), no. 2, 355--407.
MR1653320 (2000c:11108) Goncharov, A. B.(1-BRN) Multiple polylogarithms, cyclotomy and modular complexes. Math. Res. Lett. 5 (1998), no. 4, 497--516.
A. B. Goncharov, Geometry of the trilogarithm and the motivic Lie algebra of a field
A good path to an overview of polylogs could be checking everything by Goncharov, and all references in reviews of Goncharov.
arXiv:1210.2358 Classical Polylogarithm -- Abstract of a series of lectures given at the workshop on polylogs in Essen, May 1 -- 4, 1997 fra arXiv Front: math.AG av Annette Huber, Jörg Wildeshaus These are extended abstracts from an series of lectures in 1997. The text has not been updated since then.
We explain the construction of the motivic polylog as published in Annette Huber, Jörg Wildeshaus, Classical Motivic Polylogarithm According to Beilinson and Deligne, Doc.Math.J.DMV 3 (1998) 27-133. The main application is a comparison result for cyclotomic elements needed in the proof of the Tamagawa number conjecture of Bloch and Kato for Dirichlet characters. The exposition concentrates on the Hodge theoretic part of the story.arXiv:0908.2238 A simple construction of Grassmannian polylogarithms from arXiv Front: math.AG by A. B. Goncharov We give a simple explicit construction of the Grassmannian n-logarithm, which is a multivalued analytic function on the quotient of the Grassmannian of generic n-dimensional subspaces in 2n-dimensional coordinate complex vector space by the action of the 2n-dimensional coordinate torus.
We study Tate iterated integrals, which are homotopy invariant integrals of 1-forms dlog(rational functions). We introduce the Hopf algebra of integrable symbols related to an algebraic variety, which controls the Tate iterated integrals We give a simple explicit formula for the Tate iterated integrals related to the Grassmannian polylogarithms.<]]>- Polynomial functorWrite comment View comments
See Eilenberg and Mac Lane, Ann Math 1954.
Bourbaki talk by Pirashvili around 1999: review
Book: Franjou, Vincent(F-NANTC-LM); Friedlander, Eric M.(1-NW); Pirashvili, Teimuraz(GE-AOS); Schwartz, Lionel(F-PARIS13-GA). Rational representations, the Steenrod algebra and functor homology. Panoramas et Synthèshort exact sequence 16. Société Mathématique de France, Paris, 2003. xxii+132 pp. ISBN: 2-85629-159-7.
Pirashvili and Franjou: Strict polynomial functors and coherent functors.
Gambino and Kock on polynomial functors and polynomial monads http://arxiv.org/abs/0906.4931
<]]>- PolytopeWrite comment View comments
Polytopes folder
<]]>- PontryaginWrite comment View comments
Selected works, 4 vols
<]]>- Pontryagin dualityWrite comment View comments
A basic reference is Valenza-Ramakrishnan.
http://mathoverflow.net/questions/70655/discrete-compact-duality-for-nonabelian-groups
<]]>- Popescu theoremWrite comment View comments
- <]]>
- Postnikov towerWrite comment View comments
A short and beautiful exposition of Postnikov stuff and the underlying ideas is LNM0013.
A rigorous treatment is found in Jardine-Goerss chapter VI. They also discuss model structures on towers of spaces.
http://ncatlab.org/nlab/show/Postnikov+system+in+triangulated+category
Dieudonne in Panorama: The notion of fibration also enables us to characterize homotopy types by a system of invariants. Given a sequence of groups
 commutative for
commutative for 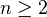 , we define a sequence of spaces
, we define a sequence of spaces  where
where 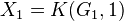 and
and 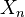 for
for 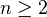 is a bundle with base
is a bundle with base 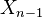 and fiber
and fiber
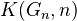 . The inverse limit
. The inverse limit  of the sequence
of the sequence 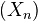 is such that
is such that 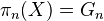 for all
for all  , and every space
, and every space 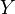 has the same homotopy type as such an
inverse limit; this homotopy type is characterized by the
has the same homotopy type as such an
inverse limit; this homotopy type is characterized by the 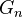 and, for each
and, for each
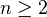 , the isomorphism class of the bundle
, the isomorphism class of the bundle 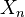 with base
with base 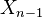 ; it can be shown that these isomorphism classes are in one-one correspondence with cohomology classes in
; it can be shown that these isomorphism classes are in one-one correspondence with cohomology classes in 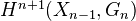 (Postnikov's construction).
(Postnikov's construction).Dwyer: Self-homotopy equivalences of Postnikov conjugates
<]]>- Pre-triangulated categoryWrite comment View comments
See Hovey p. 170. Basicly, it is an abstraction of the homotopy category of a pointed model category, with its cofiber and fiber sequences. Hovey calls it "the unstable analogue of a triangulated category".
Consider a (right) closed
 -module
-module  . We have functors:
. We have functors:
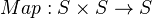
- Suspension functor:
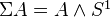
- Loop functor:
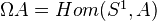
The last two are cogroup and group objects as expected.
A pretriangulation on
 is now a collection of cofiber sequences (or left triangles) and a collection of fiber sequences (or right triangles) satisfying nine axioms. To define a pretriangulated category, Hovey also requires existence of small products and coproducts.
is now a collection of cofiber sequences (or left triangles) and a collection of fiber sequences (or right triangles) satisfying nine axioms. To define a pretriangulated category, Hovey also requires existence of small products and coproducts.Can define exact adjunction between pretriangulated categories, as a pair preserving cofiber and fiber sequences, respectively.
A summarizing theorem: The homotopy pseudo-2-functor of Hovey's Theorem 5.7.3 lifts to a pseudo-2-functor from pointed model cats to pre-triangulated cats, which commutes with the duality 2-functor.
Can also define closed (central, symmetric) monoidal pre-triangulated category.
Hovey defines a triangulated category as a pre-triangulated category in which the suspension functor is an equivalence. Every triangulated category in the sense of Hovey is a triangulated category in the classical sense, but not the other way around (as shown by Muro et al). Hovey claims that "every triangulated category in nature is the homotopy category of a stable model category".
<]]>- Presentable categoryWrite comment View comments
http://ncatlab.org/nlab/show/presentable+(infinity,1)-category
http://www.ncatlab.org/nlab/show/locally+presentable+category
Peter knows everything about this and related concepts
<]]>- Presheaves of spectraWrite comment View comments
See Jardine's Fields lecture notes or some other notes
Here is an exposition of some work of Thomason.
Notes from Jardine: Generalized etale cohomology theories
See Spectrum
<]]>- Presheaves with transfersWrite comment View comments
Lots of material in MVW.
Remark in Voevodsky: Homology of schemes II, p 3 in the intro: Considering PST instead of qfh-sheaves is due to Suslin conversations, and is needed in order to get correct answers with integral coeffs.
<]]>- PridhamWrite comment View comments
- <]]>
- Prime at infinityWrite comment View comments
- <]]>
- Principal bundleWrite comment View comments
http://nlab.mathforge.org/nlab/show/principal+bundle
http://nlab.mathforge.org/nlab/show/principal+2-bundle
http://nlab.mathforge.org/nlab/show/principal+infinity-bundle
<]]>- PROWrite comment View comments
http://ncatlab.org/nlab/show/PRO
Relation to PROPs and sketches
<]]>- Profinite groupsWrite comment View comments
Book by Ribes and Zalesskii, in Group theory folder.
Serre: Galois cohomology
Cohomology of number fields?
Profinite Groups, Second edition (Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics) fra Mathematics by: Luis Ribes, Pavel Zalesskii
<]]>- Profinite homotopy typesWrite comment View comments
- <]]>
- Projection formulaWrite comment View comments
- <]]>
- PROPWrite comment View comments
[arXiv:1207.2773] On the category of props fra arXiv Front: math.AT av Philip Hackney, Marcy Robertson The category of (colored) props is an enhancement of the category of colored operads, and thus of the category of small categories. The titular category has nice formal properties: it is bicomplete and is a symmetric monoidal category, with monoidal product closely related to the Boardman-Vogt tensor product of operads. Tools developed in this article, which is the first part of a larger work, include a generalized version of multilinearity of functors, a free prop construction defined on certain "generalized graphs", and the relationship between the category of props and the categories of permutative categories and of operads.
<]]>- ProperWrite comment View comments
- <]]>
- Proper model categoryWrite comment View comments
A model category is left proper if a pushout of a WE under a cofibration is always a WE. Dually, a model category is right proper if a pullback of a WE under a fibration is always a WE. A model category is proper if it is both left proper and right proper.
http://ncatlab.org/nlab/show/proper+model+category
http://golem.ph.utexas.edu/category/2012/05/the_mysterious_nature_of_right.html
Examples of proper model cats:
 , and simplicial abelian groups.<]]>
, and simplicial abelian groups.<]]>- Properties of CTs in AGWrite comment View comments
Descent properties
Base independence, K-theory yes, etale cohomology no
Rigidity?
Purity? See Levine in handbook for B-O axioms,
See Axioms glossary entry
Cycle maps, Chern classes, induced equivalence relation
Closed M-V?
<]]>- Property structure stuffWrite comment View comments
- <]]>
- Pseudo-abelian categoryWrite comment View comments
An Additive category
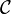 is called pseudo-abelian if of for every endomorphism
is called pseudo-abelian if of for every endomorphism 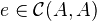 such that
such that 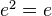 , one can write
, one can write  as a direct sum
as a direct sum 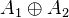 such that
such that  is the composition of the projection
is the composition of the projection 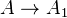 and the inclusion
and the inclusion 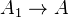 . We call
. We call 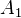 the image of
the image of  , and denote it by
, and denote it by 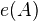 . In this situation,
. In this situation, 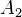 will be the image of
will be the image of  .
.Let
 be any additive category. Write
be any additive category. Write  for the category in which the objects are pairs
for the category in which the objects are pairs 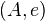 where
where  is and object of
is and object of 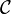 and
and  is an idempotent endomorphism of
is an idempotent endomorphism of  , and where the morphisms from
, and where the morphisms from 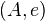 to
to 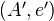 are given by the subgroup of
are given by the subgroup of 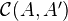 of morphisms of the form
of morphisms of the form 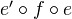 . It is easy to verify that
. It is easy to verify that 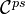 is pseudo-abelian, and we call it the pseudo-abelian envelope of
is pseudo-abelian, and we call it the pseudo-abelian envelope of 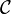 . The obvious functor
. The obvious functor 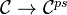 is fully faithful.
is fully faithful.Balmer and Schlichting proved that a pseudo-abelian envelope of a triangulated category is also triangulated.
<]]>- Pseudo-riemannian geometryWrite comment View comments
- <]]>
- PurityWrite comment View comments
Mentioned in Geisser in K-theory handbook. Also I think in Levine's chapter, under Bloch-Ogus axioms.
Fujiwara: A proof of the absolute purity conjecture (following Gabber)
Mentioned by Scholl in some meeeting Oct/Nov 2008
Title: Notions of purity and the cohomology of quiver moduli Authors: Michel Brion, Roy Joshua http://front.math.ucdavis.edu/1205.0629
Scholl-Deninger: The Beilinson conjectures, p 5 in the double page version. Says that weak purity for Deligne cohomology holds, meaning that for a closed subscheme Y of X of pure codim q, we have
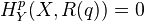 for
for 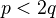 .
.arXiv:0909.0969 Purity results for $p$-divisible groups and abelian schemes over regular bases of mixed characteristic from arXiv Front: math.AG by Adrian Vasiu, Thomas Zink Let $p$ be a prime. Let $(R,\ideal{m})$ be a regular local ring of mixed characteristic $(0,p)$ and absolute index of ramification $e$. We provide general criteria of when each abelian scheme over $\Spec R\setminus{\ideal{m}}$ extends to an abelian scheme over $\Spec R$. We show that such extensions always exist if $e\le p-1$, exist in most cases if $p\le e\le 2p-3$, and do not exist in general if $e\ge 2p-2$. The case $e\le p-1$ implies the uniqueness of integral canonical models of Shimura varieties over a discrete valuation ring $O$ of mixed characteristic $(0,p)$ and index of ramification at most $p-1$. This leads to large classes of examples of Néron models over $O$. If $p>2$ and index $p-1$, the examples are new.
arXiv:1108.6250 Proof of a conjecture of Colliot-Thélène from arXiv Front: math.AG by Jan Denef We prove a conjecture of Colliot-Thélène that implies the Ax-Kochen Theorem on p-adic forms. We obtain it as an easy consequence of a diophantine purity theorem whose proof forms the body of the present paper.
<]]>- Pursuing stacksWrite comment View comments
- <]]>