Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- qfh-topologyWrite comment View comments
See Voevodsky's thesis for some material on the qfh-topology and sheaves for this topology. See also h-topology
<]]>- Quadratic formWrite comment View comments
Book by Karpenko et al: The Algebraic and Geometric Theory of Quadratic Forms
I think there are other recent books by people like maybe Kahn, Merkurjev, ...
Folder AG/Quadratic forms
Maybe there is a survey by Auel
For norm quadrics and related Bloch-Kato stuff, one place to start might be Weibel's web page. Another place is Voevodsky: Motivic cohomology with Z/2 coeffs, see pp 19 (i.e. section 4) in particular.
arXiv:1105.5759 Notes on "Quadratic Forms and Automorphic Forms" from the 2009 Arizona Winter School from arXiv Front: math.NT by Jonathan Hanke These notes are an extension of the rough notes provided for my four lecture graduate level course on "Quadratic Forms and Automorphic Forms" at the March 2009 Arizona Winter School on Quadratic Forms. They are meant to give a survey of some aspects of the classical theory of quadratic forms over number fields and their rings of integers (e.g. over Q and Z), and their connection with modular and automorphic forms.
<]]>- QuantityWrite comment View comments
- <]]>
- QuantizationWrite comment View comments
http://mathoverflow.net/questions/71484/quantization-and-noncommutative-deformations
http://mathoverflow.net/questions/8606/what-does-quantization-is-not-a-functor-really-mean
See also nlab
<]]>- Quantum Field TheoryWrite comment View comments
Folland: Quantum Field Theory: A tourist guide for mathematicians
arXiv:1109.0955 Survey of mathematical foundations of QFT and perturbative string theory from arXiv Front: math.AT by Hisham Sati, Urs Schreiber Recent years have seen noteworthy progress in the mathematical formulation of quantum field theory and perturbative string theory. We give a brief survey of these developments. It serves as an introduction to the more detailed collection "Mathematical Foundations of Quantum Field Theory and Perturbative String Theory".
Takhtajan: Quantum mechanics for mathematicians
Volumes with Deligne, maybe identical to the online seminar notes from fall and spring
nLab on higher cats in QFT
nlab factorization algebra
http://nlab.mathforge.org/nlab/show/FQFT Functorial QFT
http://ncatlab.org/nlab/show/HQFT
http://ncatlab.org/nlab/show/sigma-model
http://www.ncatlab.org/nlab/show/partition+function
Teleman, Cohen, Blumberg on Open-closed field theories, Hochschild homology, and much more: http://arxiv.org/abs/0906.5198
<]]>- Quantum groupWrite comment View comments
http://www.ncatlab.org/nlab/show/quantum+group
http://mathoverflow.net/questions/58040/groups-quantum-groups-and-fill-in-the-blank
<]]>- Quantum stuffWrite comment View comments
For quantum groups and other quantum stuff, see the Quantum stuff folder under ALGEBRA. Have not looked at this really
<]]>- Quasi-categoryWrite comment View comments
Joyal: A quasicat is a Kan complex iff its homotopy cat is a groupoid.
There is a set of notes on quasicats from a course by Joyal in Barcelona, I think Peter said he would send this at some point.
Toen: Vers une axiomatisation etc. File Toen publ ntopoi.pdf. Defines a "theory of (1-infty)-categories", and shows that any such theory is Quillen eq to complete Segal spaces. Another example of such a theory is Rezk's homotopy theory of homotopy theories.
<]]>- QuillenWrite comment View comments
- <]]>
- Quillen equivalenceWrite comment View comments
A Quillen adjunction is a Quillen equivalence if for all cofibrant
in 
, and fibrant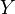 
in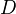 
, a map 
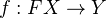is a WE in 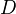if and only if 
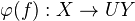is a WE in . This is the same as saying that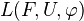 
is an adjoint equivalence of categories, which will happen if and only if 
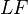is an equivalence of categories.For a criterion, see Hovey, page 21.
<]]>- Quillen functorWrite comment View comments
Definition: Let
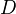, be model categories.- A functor
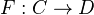is a left Quillen functor if it is a left adjoint, and preserves cofibrations and trivial cofibrations. - A functor
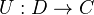is a right Quillen functor if it is a right adjoint, and preserves fibrations and trivial fibrations. - An adjunction
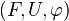is a Quillen adjunction if 
is a left Quillen functor, or equivalently, if 
is a right Quillen functor.
(Here
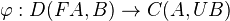is a natural isomorphism)The main point of the above definition is that a left (right) Quillen functor preserves cofibrant (fibrant) objects and WEs between them.
Notation: We write
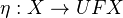for the unit map and 
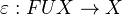for the counit map.Example: Take
to be geometric realization, and 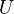to be singular complex. This gives a Quillen adjunction from 
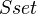to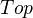 
.Example: Diagonal functor and product functor, or coproduct functor and diagonal functor.
Example: Disjoint basepoint functor and forgetful functor.
We can define the 2-category of model categories, using Quillen adjunctions as morphisms.
There is also a notion of Quillen adjunction of two variables, sometimes the left adjoint occurring in this definition is called a Quillen bifunctor. See Hovey, section 4.2.
In Goerss-Schemmerhorn, p. 20, there is a theorem describing how an adjoint pair can allow us to lift a model category structure from one category to another. Example: non-negatively graded cdga's get a model structure from the category of chain complexes, when the base field has char zero but not when it has char 2.
<]]>- A functor
- Quillen's Theorem AWrite comment View comments
http://mathoverflow.net/questions/101235/are-connected-categories-with-pullbacks-weakly-contractible
<]]>- Quillen's Theorem BWrite comment View comments
arXiv:1101.4879 A Quillen theorem Bn for homotopy pullbacks from arXiv Front: math.CT by C. Barwick, D. M. Kan We prove an extension of the Quillen Theorem Bn for homotopy fibres to a similar result for homotopy pullbacks and use this to obtain sufficient conditions on a pullback diagram of categories to guarantee that it be a homotopy pullback.
Ref: Jardine-Goerss IV.5.2. It is stated there for a functor
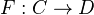between small cats satisfying some hyps, and concludes that a certain square involving BC and BD is homotopy cartesian. They also emphasize the following lemma: For a sSet-valued functor on a small cat 
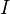sending all morphisms to weak equivalences, and for any object 
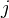of 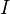, the square given by 
, 
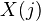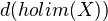, pt,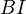 
is homotopy cartesian. Also other variations on this theme.<]]>- Quillen-Lichtenbaum conjectureWrite comment View comments
Some work on the wild kernel
<]]>- Quiver representationWrite comment View comments
Good lecture notes from a summer school.
<]]>