Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- Radditive functorsWrite comment View comments
Voevodsky: Simplicial radditive functors (2007), an improved version of Delta-closed classes (2000). Categories of simplicial radditive functors provide a context for "doing homotopy theory". Examples seem to include simplicial algebras. One of the points of this is to generate classes of morphisms which produce good localizations of the homotopy category of a category
 , defined as the homotopy category of a certain model structure on simplicial radditive functors on
, defined as the homotopy category of a certain model structure on simplicial radditive functors on  . Note: Delta-closed classes has more stuff in the introduction than the newer paper, in particular explaining how the above gives a non-additive analogue of Verdier saturation.<]]>
. Note: Delta-closed classes has more stuff in the introduction than the newer paper, in particular explaining how the above gives a non-additive analogue of Verdier saturation.<]]>- Rational homotopy theoryWrite comment View comments
Felix Oprea Tanre in Homotopy theory folder: Rational htpy, formality. Note: Compact Kahler manifolds are fomal. Last chapter: Brief mention of Gelfand-Fuchs cohomology and iterated integrals. Also brief list of refs on MHSs on homotopy groups on pp366
See the last few pages of Baues: Homotopy types, for a brief intro and references, including def of Sullivan minimal models.
Hess: Rational HT, a brief introd
http://ncatlab.org/nlab/show/rational+homotopy+theory
For a physicist's intro to rational homotopy theory, see Crane: Model categories and quantum gravity
Bousfield and Gugenheim: On PL de Rham theory and rational homotopy type. Memoirs of the AMS 8 (no el copy), 1976. "Bridges the gap between Quillen's and Sullivan's approaches to rational homotopy theory".
arXiv:1211.1647 Dewformation theory and rational homotopy type fra arXiv Front: math.AT av Mike Schlessinger, Jim Stasheff We regard the classification of rational homotopy types as a problem in algebraic deformation theory: any space with given cohomology is a perturbation, or deformation, of the "formal" space with that cohomology. The classifying space is then a "moduli" space --- a certain quotient of an algebraic variety of perturbations. The description we give of this moduli space links it with corresponding structures in homotopy theory, especially the classification of fibres spaces with fixed fibre F in terms of homotopy classes of maps of the base B into a classifying space constructed from the monoid of homotopy equivalences of F to itself. We adopt the philosophy, later promoted by Deligne in response to Goldman and Millson, that any problem in deformation theory is "controlled" by a differential graded Lie algebra, unique up to homology equivalence (quasi-isomorphism) of dg Lie algebras. Here we extend this philosophy further to control by sh-Lie-algebras.
Bousfield-Kan p 10 expresses the hope for an R-homotopy theory, for any subring R of the rationals, or for
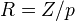 .<]]>
.<]]>- Real multiplicationWrite comment View comments
Manin: Real multiplication and noncommutative geometry. In Abel volume, under GENERAL folder
Work of Darmon???
arXiv:0910.3875 Real multiplication and modular curves from arXiv Front: math.NT by Igor Nikolaev We construct an inverse of functor F, which maps isomorphism classes of elliptic curves with complex multiplication to the stable isomorphism classes of the so-called noncommutative tori with real multiplication. The construction allows to prove, that complex and real multiplication are mirror symmetric, i.e. F maps each imaginary quadratic field of discriminant -D to the real quadratic field of discriminant D.
arXiv:0912.4905 On a noncommutative reciprocity law from arXiv Front: math.NT by Igor Nikolaev We prove a reciprocity relation, which says that an L-function of the noncommutative torus with real multiplication coincides with the Hasse-Weil L-function of an elliptic curve with complex multiplication. Our proof is based on an explicit formula for the Teichmueller functor between elliptic curves and noncommutative tori. The result entails, that the Cuntz-Krieger algebras are isomorphic to elliptic curves over finite fields.
arXiv:1104.0609 On the rank conjecture from arXiv Front: math.NT by Igor Nikolaev The rank conjecture says that rank of the elliptic curve with complex multiplication is by one less the arithmetic complexity of the corresponding noncommutative torus with real multiplication. It is proved, that the conjecture is true for infinitely many pairwise non-isomorphic curves of rank zero.
<]]>- RealizationsWrite comment View comments
See the last section of Levine's K-theory handbook chapter. He discusses "realization functors" for various kinds of categories of motives, and various cohomology theories. Seems really interesting.
Realizations can also refer to maps relating A1-homotopy theory to classical homotopy theory. See end of chapter 3 in Morel-Voevodsky: A1-homotopy theory of schemes.
K-th 992 : Réalisations des complexes motiviques de Voevodsky by Florence Lecomte and Nathalie Wach
In this paper, we construct realizations of motivic complexes over a number field. The De Rham realization is represented by a motivic De Rham complex and has a Hodge filtration. The Betti and l-adic realizations are integrally defined. When restricted to geometrical motives, the realization functors are endowed with Bondarko's weight filtration and rationally agree with Huber's realizations.
<]]>- Reciprocity lawsWrite comment View comments
Deligne: Les constantes... othogonale. The review mentions a form of the Hasse reciprocity law in which the dissymmetry between the finite and infinite places disappears.
See Hannu thesis.
Tame symbols and reciprocity laws on arithmetic surfaces. http://front.math.ucdavis.edu/1203.6712. Author: Dongwen Liu
Artin reciprocity: See Frei in Abel volume for historical background
http://mathoverflow.net/questions/96290/weil-reciprocity-vs-artin-reciprocity
arXiv:1002.4848 A categorical proof of the Parshin reciprocity laws on algebraic surfaces from arXiv Front: math.CT by Denis Osipov, Xinwen Zhu We define and study the 2-category of torsors over a Picard groupoid, a central extension of a group by a Picard groupoid, and commutator maps in this central extension. Using it in the context of two-dimensional local fields and two-dimensional adelic theory we obtain the two-dimensional tame symbol and a new proof of Parshin reciprocity laws on an algebraic surface.
arXiv:1002.2707 Non-abelian reciprocity laws on a Riemann surface from arXiv Front: math.AG by Ivan Horozov On a Riemann surface there are relations among the periods of holomorphic differential forms, called Riemann's relations. If one looks carefully in Riemann's proof, one notices that he uses iterated integrals. What I have done in this paper is to generalize these relations to relations among generating series of iterated integrals. Since the main result is formulated in terms of generating series, it gives infinitely many relations - one for each coefficient of the generating series. The lower order terms give the well known classical relations. The new result is reciprocity for the higher degree terms, which give non-trivial relations among iterated integrals on a Riemann surface. As an application we refine the definition of Manin's noncommutative modular symbol in order to include Eisenstein series. Finally, we have to point out that this paper contains some constructions needed for multidimensional reciprocity laws like a refinement of one of the Kato-Parshin reciprocity laws.
arXiv:1209.1217 K-groups of reciprocity functors from arXiv Front: math.AG by Florian Ivorra, Kay Rülling In this work we introduce reciprocity functors, construct the associated K-group of a family of reciprocity functors, which itself is a reciprocity functor, and compute it in several different cases. It may be seen as a first attempt to get closed to the notion of reciprocity sheaves imagined by B. Kahn. Commutative algebraic groups, homotopy invariant Nisnevich sheaves with transfers, cycle modules or Kähler differentials are examples of reciprocity functors. As commutative algebraic groups do, reciprocity functors are equipped with symbols and satisfy a reciprocity law for curves.
arXiv:1206.5817 Reciprocity Laws on Algebraic Surfaces via Iterated Integrals from arXiv Front: math.AG by Ivan Horozov, Matt Kerr In this paper we define a new symbol, called the 4-function symbol, on a complex algebraic surface, which satisfies two types of reciprocity laws. In comparison the Parshin symbol on a surface is defined for 3 non-zero rational functions. Both the 4-function symbol and the Parshin symbol are expressed as a product of more primitive symbols, which we call bi-local symbols. They also satisfy reciprocity laws and occur naturally, when iterated integrals are used. The key technical ingredient is the notion of iterated integrals on membranes. In terms of such integrals, we not only prove reciprocity laws but we give an interpretation of the symbols as parallel transports on the loop space of a variety. Moreover, such integrals give a relation between the 4-function symbol and the Riemann curvature tensor.
The appendix contains a K-theoretic variant of the 4-function symbol, which differs by a sign. This difference causes one of the reciprocity laws to fail, suggesting that iterated integrals play an essential role in the definition of the (correct) 4-function symbol.<]]>- Recognition principleWrite comment View comments
http://mathoverflow.net/questions/22585/algebras-over-the-little-disks-operad
Here is a quote from somewhere (forgot where): For extending the theory of triangulated motives from varieties to general schemes, the main remaining problem is finding a good recognition principle for T-loop spaces.
<]]>- Red shift conjectureWrite comment View comments
Ref Ausoni and Rognes: The chromatic red shift in algebraic Kth.
Toen: Note of Chern character, loop spaces and derived algebraic geometry. File Toen web publ Abel-2007.pdf. See Derived categorical sheaves for more about this article.
Preprint in progress of Rognes: Higher red-shift
<]]>- Reedy categoryWrite comment View comments
http://ncatlab.org/nlab/show/Reedy+category
http://www.ncatlab.org/nlab/show/Reedy+model+structure
More on Reedy model str in Goerss-Jardine chapter VII.
<]]>- Regular categoryWrite comment View comments
Regular category: See Borceaux vol 2, or maybe nlab. Every topos is a regular category.
<]]>- RegularizationWrite comment View comments
See Deninger's articles.
Zeta regularisation: Book by Elizalde in L-functions folder
http://mathoverflow.net/questions/183/zeta-function-regularization-of-determinants-and-traces
http://mathoverflow.net/questions/94512/understanding-zeta-function-regularization
arXiv:1303.7028 Zeta regularized products, Riemann zeta zeros and prime number spectra
<]]>- RegulatorWrite comment View comments
We refer to the following different types of regulators:
- "Ordinary" regulators, temporarily placed under Absolute Hodge cohomology
- p-adic regulators
- syntomic regulators, see Syntomic cohomology
Burgos: The regulators of Borel and Beilinson. Available online somewhere
Ramakrishnan: Regulators, algebraic cycles, and values of L-functions (1989)
See Goncharov in K-theory handbook.
Kuzmin has several papers with something like "remarks on the l-adic regulator" in the title. One is from 2009 in Izvestiya
http://mathoverflow.net/questions/34801/dirichlets-regulator-vs-beilinsons-regulator
Have gone through a MathSciNet search on regulator AND cohomology
<]]>- Regulators references IIWrite comment View comments
arXiv:1007.1385 The Relative Chern Character and Regulators from arXiv Front: math.KT by Georg Tamme In this thesis we construct a modified version of Karoubi's relative Chern character for smooth varieties over the complex numbers or the ring of integers in a p-adic number field. Comparison results with the Deligne-Beilinson Chern character and the p-adic Borel regulator constructed by Huber and Kings are proven. As a corollary we obtain a new proof of Burgos' theorem that Borel's regulator is twice Beilinson's regulator.
<]]>- Relative algebraic geometryWrite comment View comments
See Toen: Essen talk. Main idea: Replace rings by commutative monoids in any symmetric monoidal category. Get new notion of schemes, in some sense. Examples include super-schemes, algebraic geom over a Tannakian cat, and hopefully schemes over F1. Nontrivial to find the right notion of topology, to enable glueing.
Toen and Vaquie: Under Spec Z. Some notes: Idea: Relative alg geom. Think of commutative monoids in a symm monoidal cat C as models for affine schemes relative to C. If there is a reasonable symmetric monoidal functor from C to Z-modules, get a base change functor, and a notion of scheme under Spec(Z). Homotopical version of this requires C to have a model structure. Now have flat and Zariski topology. Can make sense of schemes: a functor with a Zariski covering. Stuff about toric varieties and GL. Brave new AG over the sphere spectrum, and the spectrum with one element. Digression: Flat and Zariski ok. For etale (and maybe hence Nisnevich), Peter Arndt said there might be three ways of doing it: by a lifting property, by factorization systems (Anel), or by mimicking something Deitmar does for monoids, see Peter's thesis in progress, and see also the notion of formally etale.
<]]>- Relative cyclesWrite comment View comments
- <]]>
- RenormalizationWrite comment View comments
Many books available.
<]]>- Representability in algebraic geometryWrite comment View comments
See notes by Deligne/Voevodsky for a proof of the fact that the Eilenberg-MacLane spectrum represents motivic cohomology.
The etale preprint of Quick
The preprint of Jardine treating abstract representability theorems for stable model cats
Hornbostel on hermitian K-theory and Witt groups
Possibly the following fact is of interest: The contravariant functor from
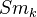 to Huber's triangulated tensor category of mixed motives extend to a functor on smooth simplicial schemes over
to Huber's triangulated tensor category of mixed motives extend to a functor on smooth simplicial schemes over  . See Levine in K-theory handbook, page 475.
. See Levine in K-theory handbook, page 475. Consequences of representability
Yagunov on rigidity for theories represented by T-spectra. This seems to be generalized here
<]]>- Representability theoremsWrite comment View comments
Check Murfet's notes on Algebra in a category. Can the notion of a module here be used to think about representing objects for functors landing a category of representations of a group, for example the absolute Galois group???
There is the following theorem: Consider a (contravariant???) setvalued functor on a Grothendieck category. It is representable iff it commutes with small projective limits.
An interesting article by Chorny on representability for space-valued functors, also relating representability in the contravariant case to something analogous to Goodwillie calculus.
<]]>- Representable functorWrite comment View comments
- <]]>
- Representation theoryWrite comment View comments
See Rep theory folder
http://mathoverflow.net/questions/2755/a-learning-roadmap-for-representation-theory
http://nlab.mathforge.org/nlab/show/representation+theory
[arXiv:0912.0569] Lectures on geometric constructions of the irreducible representations of GL_n
Old list of books on rep th and algebraic groups:
las conrad o rubin!!!
Lie Groups and Automorphic Forms (AMS/IP Studies in Advanced Mathematics) (Paperback)
Serre: Linear reps of finite groups
Knapp
Fulton and Harris
Borel: linear algebraic groups Jantzen: Reps of alg groups, 2nd ed
Humphreys: Intro to Lie groups and algebraic groups
Humpreys: Linear algebraic groups
humphreys: Intro to Lie algs and rep th
Serre: algebraic groups and class fields
<]]>- Resolution of singularitiesWrite comment View comments
Folder: AG/RoS
De Jong on alterations. Is this the same as this article?
Geisser on applications of alterations. This was published in some volume on RoS, I think
A nice book review
Berthelot: Alterations de varietes algebriques (1997, sem. Bourbaki)
Abyankhar: Resolution of singularities of embedded algebraic surfaces (Springer, 1998)
Lipman: Review of "Canonical desingularization..."
Kollar: The structure of algebraic three-folds: An introduction to Mori's program
Villamayor: Constructiveness of Hironaka's resolution
A very good book: Resolution of singularities
Temkin on functorial desingularization of quasi-excellent schemes in char zero.
Resolution of Singularities - Steven Dale Cutkosky
http://mathoverflow.net/questions/4612/hironaka-desingularisation-theorem-new-proofs-in-literature
Lunts: Categorical ROS: http://arxiv.org/pdf/0905.4566v1
Voevodsky's ICM talk, section 7, mentions work of Bloch in Moving lemma for higher Chow groups, using Spivakovsky's solution to Hironaka's polyhedra game, which could maybe allow you to circumvent lack of RoS sometimes.
http://front.math.ucdavis.edu/1002.2651 Bondarko's application of a RoS result of Gabber (2011).
arXiv:1103.3464 Techniques for the study of singularities with applications to resolution of 2-dimensional schemes from arXiv Front: math.AG by Angélica Benito, Orlando E. Villamayor We give an overview of invariants of algebraic singularities over perfect fields. We then show how they lead to a synthetic proof of embedded resolution of singularities of 2-dimensional schemes.
arXiv:1104.0325 Some natural properties of constructive resolution of singularities from arXiv Front: math.AG by Angélica Benito, Santiago Encinas, Orlando E. Villamayor U These expository notes, addressed to non-experts, are intended to present some of Hironaka's ideas on his theorem of resolution of singularities. We focus particularly on those aspects which have played a central role in the constructive proof of this theorem.
In fact, algorithmic proofs of the theorem of resolution grow, to a large extend, from the so called Hironaka's fundamental invariant. Here we underline the influence of this invariant in the proofs of the natural properties of constructive resolution, such as: equivariance, compatibility with open restrictions, with pull-backs by smooth morphisms, with changes of the base field, independence of the embedding, etc.<]]>- Retract argumentWrite comment View comments
In any category, if
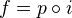 and
and  has the LLP wrt
has the LLP wrt 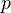 , then
, then  is a retract of
is a retract of 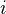 . Dually, if
. Dually, if  has the RLP wrt
has the RLP wrt 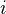 , then
, then  is a retract of
is a retract of 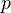 .
.This implies that a map is a cofib (trivial cofib) iff it has the LLP wrt all trivial fibs (fibs), and the dual statement.
<]]>- RezkWrite comment View comments
- <]]>
- RiemannWrite comment View comments
Book by Laugwitz, biography probably, English translation exists.
Collected papers, one large volume
<]]>- Riemann hypothesisWrite comment View comments
Book by Borwein et al. No el copy, check gig.
RH: Bombieri's Clay formulation
http://mathoverflow.net/questions/17209/consequences-of-the-riemann-hypothesis
Surveys in noncomm geom: Contains two chapters on RH
arXiv:0908.2909 Abstract intersection theory and operators in Hilbert space from arXiv Front: math.NT by Grzegorz Banaszak, Yoichi Uetake For an operator of a certain class in Hilbert space, we introduce axioms of an abstract intersection theory, which we prove to be equivalent to the Riemann Hypothesis concerning the spectrum of that operator. In particular if the nontrivial zeros of the Riemann zeta-function arise from an operator of this class, the original Riemann Hypothesis is equivalent to the existence of an abstract intersection theory.
[arXiv:1002.4127] More than 41% of the zeros of the zeta function are on the critical line from arXiv Front: math.NT by Hung Bui, Brian Conrey, Matthew Young We prove that more than 41% of the zeros of the zeta function are on the critical line.
On axioms for intersection theory for operators: http://front.math.ucdavis.edu/1210.3526
arXiv:1206.2040 A local field approach to the Riemann Hypothesis from arXiv Front: math.NT by David Goss Since the seminal work of Wan, Poonen, and Sheats in the 1990's, we have been searching for the correct general statement of the Riemann Hypothesis ("RH") which appears implicit in their results. Recently, upon viewing the extension $\C/\R$ in light of results derived for the Carlitz module, we were led to view the RH as a statement about ramification which we explore in this short work. We shall see that, combined with some ideas flowing from the proofs of Wan, Poonen, and Sheats, this ramification idea has a good deal of explanatory power in finite characteristic. Indeed, unramified extensions of nonarchimedean local fields are cyclotomic in nature and this fits perfectly with the best possible extension of the result of Wan and Sheats. The notion that the zeroes "lie on a line" seems to be the beginning of the story in finite characteristic, and we show how this fits with having the zeroes be unramified.
<]]>- Riemann-Hilbert correspondenceWrite comment View comments
A Riemann Hilbert correspondence for infinity local systems
A good introduction might be found in Sabbah: Isomonodromic etc. In folder AG/Various
<]]>- Riemann-Roch IIWrite comment View comments
http://mathoverflow.net/questions/110339/riemann-roch-for-zero-cycles-on-a-surface
arXiv:1211.1783 The arithmetic Grothendieck-Riemann-Roch theorem for general projective morphisms fra arXiv Front: math.AG av José Ignacio Burgos Gil, Gerard Freixas i Montplet, Razvan Litcanu The classical arithmetic Grothendieck-Riemann-Roch theorem can be applied only to projective morphisms that are smooth over the complex numbers. In this paper we generalize the arithmetic Grothendieck-Riemann-Roch theorem to the case of general projective morphisms between regular arithmetic varieties. To this end we rely on the theory of generalized analytic torsion developed by the authors.
<]]>- Riemann-Roch theoremWrite comment View comments
Fulton and Lang: Riemann-Roch algebra.
http://mathoverflow.net/search?q=Riemann-Roch
Soulé, Gillet???
Soulé in Asterisque 311: Genres de Todd etc. "The paper starts with a lucid introduction to Arakelov geometry, arithmetic Riemann-Roch, and equivariant RR"
Faltings.
Hirzebruch: Top methods in AG. In folder AG/Various. Covers the Todd genus, and talks about RR.
Notes by Roy Smith in folder AG/Various
Baum, Fulton, MacPherson: Riemann-Roch for singular varieties (1975)
DeLand statement and proof sketch
Chern classes and RR formalism at Concrete Nonsense
Toen preprint: Notes sure la G-théorie... file Toen web unpubl gtdm.pdf. Dsicusses RR formula for stacks, the rational G-theory spectrum of DM stacks over general bases, equivariant K-th.
Toen: Thm de RR pour les champs de DM. File Toen web publ rrchamp.pdf. Discusses K-theory and RR for DM stacks, but also various notions of descent, including basic stuff on simplicial presheaves, homological descent, and etale descent.
RR for stacks, see Toen thesis, under Toen web unpubl folder.
Gillet and Soulé: On the number of lattice points etc, has a kind or RR thm, but also an erratum in 2009. MR1135244
Kim should know about arithmetic RR theorems.
LNM0210 Eichler: Projective varieties and modular forms. Studies RR with the Dedekind-Weber approach (which allows for singularities) rather than the Weil approach. Applications to varieties of Siegel and Hilbert modular forms, also def and brief intro to these kinds of forms.
Riou on RR theorem via A1-homotopy theory: http://front.math.ucdavis.edu/0907.2710
http://mathoverflow.net/questions/10630/why-todd-classes-appear-in-grothendieck-riemann-roch-formula
http://mathoverflow.net/questions/11746/is-there-grothendieck-riemann-roch-for-abelian-category
arXiv:0907.2710 Algebraic K-theory, A^1-homotopy and Riemann-Roch theorems from arXiv Front: math.AG by Joël Riou. In this article, we show that the combination of the constructions done in SGA 6 and the A^1-homotopy theory naturally leads to results on higher algebraic K-theory. This applies to the operations on algebraic K-theory, Chern characters and Riemann-Roch theorems.
arXiv:1205.0266 The excess formula in functorial form from arXiv Front: math.AG by Dennis Eriksson This article is motivated by the need for better understanding of refined Riemann-Roch theorems and the behavior of the determinant of the cohomology. This poses a certain problem of functoriality and can be understood as that of giving refined constructions of operations in algebraic $K$-theory. In this article this is specialized to mean refining the excess formula, which measures the failure of base change, to the level of Deligne's virtual category. We give a natural set of properties for such a refinement, and prove that there exists a unique family of excess formulas on this refined level satisfying these properties.
<]]>- Riemannian geometryWrite comment View comments
Berger: A panoramic view of Riemannian geom.
http://www.ncatlab.org/nlab/show/Riemannian+manifold
See Riemannian geometry folder. Note in particular Berger: Panoramic view etc.
<]]>- Right homotopyWrite comment View comments
Dual to Left homotopy. (Map from
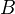 to a path object for
to a path object for  such that...)<]]>
such that...)<]]>- Rigid analytic geometryWrite comment View comments
Some notes by Kedlaya. Some motivation.
http://nlab.mathforge.org/nlab/show/rigid+analytic+geometry
I think rigid analytic geometry is mentioned as an example in Higher topos theory
Ask Michael for other notes.
What is rigid analytic geometry? One ref is Bosch, Guntzer and Remmert: Non-archimedean analysis. Springer, 1984.
MR review of the book of Huber MR1734903. At least five frameworks for non-Archimedean anlytic geometry: Tate's rigid analytic approach, Raynaud's formal scheme approach, Berkovich spaces, and Fujiwara's Zariski-Riemann spaces. To this one should maybe add perfectoid spaces, or maybe they are a subclass of adic spaces. For the relation between these notions, see the review and Scholze's first IHES lecture.
<]]>- Rigid geometryWrite comment View comments
Bosch, S., L¨utkebohmert, W.: Formal and rigid geometry I. Math. Ann. 295, 291–317 (1993) MR1202394 (94a:11090)
arXiv:1009.1056 Uniformly rigid spaces from arXiv Front: math.AG by Christian Kappen We define a new category of non-archimedean analytic spaces over a complete discretely valued field, which we call uniformly rigid. It extends the category of rigid spaces, and it can be described in terms of bounded functions on products of open and closed polydiscs. We relate uniformly rigid spaces to their associated classical rigid spaces, and we transfer various constructions and results from rigid geometry to the uniformly rigid setting. In particular, we prove an analog of Kiehl's patching theorem for coherent ideals, and we define the uniformly rigid generic fiber of a formal scheme of formally finite type. This uniformly rigid generic fiber is more intimately linked to its model than the classical rigid generic fiber obtained via Berthelot's construction.
S. Bosch, Lectures on Formal and Rigid Geometry. Preprint, 2005. Available at: http://wwwmath1.unimuenster.de/sfb/about/publ/bosch.html
S. Bosch, U. Guntzer, R. Remmert, Non-Archimedean analysis. A systematic approach to rigid analytic geometry. Grundlehren der Mathematischen Wissenschaften, 261. Springer-Verlag, Berlin, 1984. Available online.
J. Fresnel, M. van der Put, Rigid analytic geometry and its applications. Progress in Mathematics, 218. Birkhauser Boston, Inc., Boston, MA, 2004.
Berkovich: Spectral theory and analytic geometry over non-Arch etc. Mathematical Surveys and Monographs 33
<]]>- RigidificationWrite comment View comments
arXiv:1206.0422 Rigidification of algebras over essentially algebraic theories from arXiv Front: math.AT by J. Rosicky Badzioch and Bergner proved a rigidification theorem saying that each homotopy simplicial algebra is weakly equivalent to a simplicial algebra. The question is whether this result can be extended from algebraic theories to finite limit theories and from simplicial sets to more general monoidal model categories. We will present some answers to this question.
<]]>- RigidityWrite comment View comments
Sometimes refers to the behaviour of cohomology under base change between separably closed fields. I think this is true for etale and unramified cohomology. Suslin proved something for K-theory with coefficients, and Lecomte something for Chow groups.
<]]>- Ring spectrumWrite comment View comments
http://nlab.mathforge.org/nlab/show/ring+spectrum
Nice answer on intuition for ring spectra: http://mathoverflow.net/questions/82485/dedekind-spectra
Lurie: Elliptic cohomology. Mentions three possible notions of ring spectra I think.
Introduction in Greenlees: Spectra for commutative algebraists (Homotopy theory folder). Applications: Section 6A discussion Topological HH, section 6B discusses trace maps.
Roendigs et al: Motivic strict ring models for K-theory
http://front.math.ucdavis.edu/0912.4346 Units of equivariant ring spectra, by Santhanam
http://mathoverflow.net/questions/433/e-infty-spectrum-corresponding-to-zp contains some interesting ideas on pro-objects in spectra and p-adic topologies, and module categories over spectra.
Structured Ring Spectra (London Mathematical Society Lecture Note Series) fra Mathematics by: Andrew Baker, Birgit Richter
Naumann in talk July 2009: Given a ring cohomology th, Brown rep gives a spectrum, but in general we cannot say that it is a ring spectrum, because of the possible problem of phantom maps. Hopkins have showed that in classical stable htpy th, there are no even-degree phantom maps between Landweber exact spectra, although I think there might be odd degree (example given in talk). We don't have a general analogue of Hopkins' result in the motivic setting, but we can treat relevant special cases.
arXiv:1001.0902 Homological dimensions of ring spectra from arXiv Front: math.AT by Mark Hovey, Keir Lockridge We define homological dimensions for S-algebras, the generalized rings that arise in algebraic topology. We compute the homological dimensions of a number of examples, and establish some basic properties. The most difficult computation is the global dimension of real K-theory KO and its connective version ko at the prime 2. We show that the global dimension of KO is 1, 2, or 3, and the global dimension of ko is 4 or 5.
arXiv:1004.0006 The smash product for derived categories in stable homotopy theory from arXiv Front: math.AT by Michael A. Mandell 1 person liked this An E1 (or A-infinity) ring spectrum R has a derived category of modules DR. An E2 structure on R endows DR with a monoidal product. An E3 structure on R endows the monoidal product with a braiding. If the E3 structure extends to an E_4 structure then the braided monoidal product is symmetric monoidal.
arXiv:1208.6005 Constructing model categories with prescribed fibrant objects from arXiv Front: math.CT by Alexandru E. Stanculescu We put a model category structure on the category of small categories enriched over a suitable monoidal simplicial model category. For this we use the model structure on small simplicial categories due to J. Bergner and a weak form of a recognition principle for model categories due to J.H. Smith. We give an application of this weak form of Smith's result to left Bousfield localizations of categories of monoids in a suitable monoidal model category.
<]]>- RiouWrite comment View comments
- <]]>
- RoendigsWrite comment View comments
- <]]>
- RognesWrite comment View comments
- <]]>
- RosenschonWrite comment View comments
- <]]>
- RosslerWrite comment View comments
- <]]>
- RostWrite comment View comments
- <]]>
- RussianWrite comment View comments
Gould: Russian for the mathematician
<]]>- RydhWrite comment View comments
- <]]>