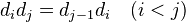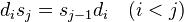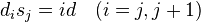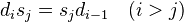Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- S-categoryWrite comment View comments
A little info is found in Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. S-cats are closely related to Segal cats.
<]]>- S-modulesWrite comment View comments
- <]]>
- SAGEWrite comment View comments
- <]]>
- SaitoWrite comment View comments
There are many mathematicians with the name Saito.
Shuji Saito
Takeshi Saito
arXiv (not all these are by the "right" Takeshi Saito.
- T. Saito: Weight spectral sequences and independence of l (2003)
Morihiko Saito
- On the formalism of mixed sheaves, RIMS-preprint 784, Kyoto Univ., Kyoto, 1991; per bibl.
Publications of some Saito:
- Arithmetic mixed Hodge structures. Check also the references linked to in this page
- Bloch's conjecture, Deligne cohomology, and Higher Chow groups
<]]>- SarnakWrite comment View comments
- <]]>
- SchechtmanWrite comment View comments
- <]]>
- Schematic homotopy typeWrite comment View comments
See Toen AIM talk on Homotopy types of algebraic varieties.
Toen, Katzarkov, Pantev: Schematic homotopy types and nonabelian Hodge theory. File Toen web publ nht.pdf. Constructs a "Hodge decomposition" (a certain action) on the schematic homotopy type of a smooth projective complex variety. This recovers many other Hodge invariants, short review of these.
http://www.ncatlab.org/nlab/show/schematic+homotopy+type
TKP: Algebraic and topological aspects etc. File Toen web publ small.pdf. Discusses various things related to schematic htpy types, including two types of algebraic models.
Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Treats general philosophical background, various forms of homotopy theories, Segal categories, Waldhausen Kth briefly, Hochshild cohomology of Segal categories and of model cats, S-cats, Segal topoi, Tannakian duality for Segal cats, and schematic homotopy types. Also letter to May about n-cats.
Toen lecture at MSRI, see file Toen web unpubl msri2002-2.pdf.
Toen: Champs affines. File Toen web publ chaff.pdf. Among other things, contains constructions of schematic homotopy types for the classical cohomologies (Betti, de Rham, Hodge, crystalline, l-adic), extending the classical notions of fundamental group. Also stuff on rational homotopy theory and p-adic homotopy theory, nonabelian Abel-Jacobi map and nonabelian period, and much more on schematic homotopy types and stacks.
Toen: Higher and derived stacks, a global overview. File web publ seatt.pdf. Also contains an intro to Segal cats, and some material on schematic homotopy types.
Question for Toen in Seville: Do schematic homotopy types only make sense for smooth projective vars? Answer: No, this should not be essential. Reason for assuming proj was that Higgs bundle correspondence was not worked out in the general case, but this has now been done by Mochizuki. Pridham has done stuff on the singular case. See also Olsson: "towards p-adic homotopy", and "F-isocristal".
arXiv:0912.4844 The de Rham homotopy theory and differential graded category from arXiv Front: math.AT by Syunji Moriya 1 person liked this This paper is a generalization of arXiv:0810.0808. We develop the de Rham homotopy theory of not necessarily nilpotent spaces, using closed dg-categories and equivariant dg-algebras. We see these two algebraic objects correspond in a certain way. We prove an equivalence between the homotopy category of schematic homotopy types and a homotopy category of closed dg-categories. We give a description of homotopy invariants of spaces in terms of minimal models. The minimal model in this context behaves much like the Sullivan's minimal model. We also provide some examples. We prove an equivalence between fiberwise rationalizations and closed dg-categories with subsidiary data.
<]]>- SchmidtWrite comment View comments
Selected publications:
- An arithmetic site for the rings of integers of algebraic number fields
- Cohomology of number fields (book)
Most papers probably accessible via http://www.mathematik.uni-regensburg.de/Schmidt/papers/schmidt04-en.html but with the two-digit number changed
<]]>- Scholbach conjectureWrite comment View comments
arXiv:1003.1215 Special L-values of geometric motives from arXiv Front: math.NT by Jakob Scholbach This paper proposes a conjecture about special values of L-functions of geometric motives over Z. We conjecture the following: the pole order of the L-function L(M, s) of M at s=0 is given by the negative Euler characteristic of motivic cohomology of $D(M) := M\dual(1)[2]$. Up to a nonzero rational factor, the L-value at s=0 is given by the determinant of a pairing coupling an Arakelov-like variant of motivic cohomology of M with the motivic cohomology of D(M). Under standard assumptions concerning mixed motives over Q, finite fields and Z, this conjecture is essentially equivalent to the conjunction of Soulé's conjecture about pole orders of $\zeta$-functions of schemes over Z, Beilinson's conjecture about special L-values for motives over Q and the Tate conjecture over F_p.
<]]>- SchollWrite comment View comments
- <]]>
- Schottky problemWrite comment View comments
arXiv:1009.0369 The Schottky Problem from arXiv Front: math.AG by Samuel Grushevsky In this survey we discuss some of the classical and modern methods in studying the (Riemann-)Schottky problem, the problem of characterizing Jacobians of curves among principally polarized abelian varieties. We present many of the recent results in this subject, and describe some directions of current research. This paper is based on the talk given at the "Classical algebraic geometry today" workshop at MSRI in January 2009.
<]]>- Schubert calculusWrite comment View comments
Kleiman, S. L.; Laksov, Dan Schubert calculus. Amer. Math. Monthly 79 (1972), 1061--1082 review
<]]>- SchwedeWrite comment View comments
- <]]>
- Section conjectureWrite comment View comments
Grothendieck's section conjecture.
A thematic program at INI
<]]>- SegalWrite comment View comments
- <]]>
- Segal categoryWrite comment View comments
Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Treats general philosophical background, various forms of homotopy theories, Segal categories, Waldhausen Kth briefly, Hochshild cohomology of Segal categories and of model cats, S-cats, Segal topoi, Tannakian duality for Segal cats, and schematic homotopy types. Also letter to May about n-cats.
Toen: Segal topoi and stacks over Segal categories. File Toen web prepr msri.pdf. Analogous and in some sense equivalent to the notion of model topos, but some advantages. Includes a Giraud type statement characterizing Segal topoi among Segal cats. Notion of homotopy type of a Segal site, improving on the etale homotopy theory of schemes, and more generally on the theory of homotopy types of sites as defined by Artin and Mazur.
Toen: Higher and derived stacks, a global overview. File web publ seatt.pdf. Also contains an intro to Segal cats, and some material on schematic homotopy types.
http://nlab.mathforge.org/nlab/show/Segal+category
A quote from somewhere: "K-theory is an invariant of Segal cats but not of triangulated categories". Can also define Hochschild cohomology of Segal cats (and of model cats!): it is the simplicial set
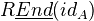 <]]>
<]]>- Seiberg-Witten invariantsWrite comment View comments
Seiberg-Witten invariants: See Taubes in Symplectic folder
<]]>- SelbergWrite comment View comments
Collected papers, 2 vols
<]]>- Selmer groupWrite comment View comments
Saito and Langer in Duke J 1996 prove a strange finiteness result for certain Selmer groups.
arXiv:1205.4456 Generalized explicit descent and its application to curves of genus 3 from arXiv Front: math.AG by Nils Bruin, Bjorn Poonen, Michael Stoll We introduce a common generalization of essentially all known methods for explicit computation of Selmer groups, which are used to bound the ranks of abelian varieties over global fields. We also simplify and extend the proofs relating what is computed to the cohomologically-defined Selmer groups. Selmer group computations have been practical for many Jacobians of curves over Q of genus up to 2 since the 1990s, but our approach is the first to be practical for general curves of genus 3. We show that our approach succeeds on some genus-3 examples defined by polynomials with small coefficients.
arXiv:1108.3364 Unfaking the fake Selmer group from arXiv Front: math.AG by Michael Stoll, Ronald van Luijk For any abelian variety J over a global field k and an isogeny phi: J -> J, the Selmer group Sel^phi(J,k) is a subgroup of the Galois cohomology group H^1(Gal(k^s/k),J[phi]), defined in terms of local data. When J is the Jacobian of a cyclic cover of P^1, the Selmer group has a quotient by a subgroup of order at most 2 that is isomorphic to the "fake Selmer group", whose definition is more amenable to explicit computations. In this paper we define in the same setting the `unfake Selmer group', which is isomorphic to the Selmer group itself and just as amenable to explicit computations as the fake Selmer group.
arXiv:1301.4724 Selmer groups as flat cohomology groups fra arXiv Front: math.AG av Kestutis Cesnavicius Given a prime number p, Bloch and Kato showed how the p^\infty-Selmer group of an abelian variety A defined over a number field K is determined by the p-adic Tate module T_p(A). In general one cannot hope that the p^m-Selmer group of A would be determined by the mod p^m Galois representation A[p^m]. We show, however, that this is the case if p is large enough. More precisely, we determine a finite explicit set of primes S depending on K and A, such that the p^m-Selmer group of A is determined by A[p^m] for all p not in S. To do this we observe that for such p, the p^m-Selmer group agrees with the flat cohomology group of the ring of integers of K with coefficients in the p^m-torsion of the Neron model of A. We give a Selmer-type description for this flat cohomology group in terms of local conditions, which, for p not in S, agree with the local conditions defining the p^m-Selmer group and depend only on A[p^m].
<]]>- Selmer varietyWrite comment View comments
See work of Minhyong Kim et al on his webpage and arxiv.
<]]>- Semiabelian categoryWrite comment View comments
Semiabelian cats: Really nice intro with good refs by Hartl and Loiseau: http://arxiv.org/pdf/0905.4941v2
<]]>- Semistable reductionWrite comment View comments
arXiv:0909.4425 Reduction of Abelian Varieties and Grothendieck's Pairing from arXiv Front: math.AG by Klaus Loerke We prove that abelian varieties of small dimension over discrete valuated, stricty henselian ground fields with perfect residue class field obtain semistable reduction after a tamely ramified extension of the ground field. Using this result we obtain perfectness results for Grothendieck's pairing.
http://mathoverflow.net/questions/77444/semistable-reduction-theorem-over-higher-dimensional-schemes
http://mathoverflow.net/questions/110810/dual-reduction-graph-of-a-curve
[arXiv:1207.1048] A tour of stable reduction with applications fra arXiv Front: math.AG av Sebastian Casalaina-Martin The Deligne-Mumford stable reduction theorem asserts that for a family of stable curves over the punctured disk, after a finite base change, the family can be completed in a unique way to a family of stable curves over the disk. In this survey, we discuss stable reduction theorems in a number of different contexts. This includes a review of recent results on abelian varieties, canonically polarized varieties, and singularities. We also consider the Semi-Stable Reduction Theorem and results concerning simultaneous stable reduction.
<]]>- Semitopological algebraic geometryWrite comment View comments
arXiv:1001.2355 Semi-topological algebraic geometry and Riemann-Roch theorem from arXiv Front: math.KT by J. H. Teh We consider algebraic varieties parametrized continuously by topological spaces. The schemes formed are non-Noetherian but they appear naturally in many places. We define Lawson homology, morphic cohomology, construct Chern classes and develop some intersection theory for semi-topological schemes. A Grothendieck-Riemann-Roch type theorem in morphic cohomology for some closed imbeddings is proved. Some new invariants like semi-topological cobordism groups, semi-topological Chow groups and higher derived categories of coherent sheaves are defined.
<]]>- SerreWrite comment View comments
- <]]>
- Serre fibrationWrite comment View comments
- <]]>
- Serre spectral sequenceWrite comment View comments
Jardine-Goerss chapter IV.
<]]>- Serre's finiteness theoremWrite comment View comments
- <]]>
- Set theoryWrite comment View comments
Lots of unlinked stuff on nLab, see for example inaccessible cardinal
I think there are good explanations of some things about cardinals in Lurie somewhere.
<]]>- Several complex variablesWrite comment View comments
See Complex manifolds folder, and maybe also Analysis folder
<]]>- SeveriWrite comment View comments
Opere Matematiche, 6 volumes
<]]>- ShafarevichWrite comment View comments
Collected mathematical papers, one vol.
<]]>- Shape theoryWrite comment View comments
- <]]>
- Sheaf theoryWrite comment View comments
I think it is true in general that sheafification is left adjoint to inclusion, and commutes with all limits and colimits.
To a sheaf of sets, one can associate a sheaf of abelian groups: Compose with the free abelian group functor, and then sheafify (Voevodsky thesis, p 2). This is the left adjoint to the forgetful functor from abelian sheaves to sheaves of sets. This is an example of a functor from sheaves of sets to sheaves of something else, which is needed if one wants to embed a category into a category behaving like "something else", in this case an abelian category. For basic properties of these abelian sheaves, see p 2 in the thesis (right exactness, preserves monos, "no torsion", flatness, respects prod and coprod). More basic properties of these sheaves, in section 2.
http://ncatlab.org/nlab/show/sheafification
http://mathoverflow.net/questions/51467/naturality-of-the-associated-sheaf
http://www.ncatlab.org/nlab/show/local+isomorphism
http://ncatlab.org/nlab/show/abelian+sheaf
http://ncatlab.org/nlab/show/quasicoherent+sheaf
http://ncatlab.org/nlab/show/IPC-property
http://www.ncatlab.org/nlab/show/restriction+and+extension+of+sheaves
http://ncatlab.org/nlab/show/category+of+sheaves
http://www.ncatlab.org/nlab/show/local+epimorphism
http://ncatlab.org/nlab/show/fine+sheaf
http://www.ncatlab.org/nlab/show/Q-category
http://golem.ph.utexas.edu/category/2010/02/sheaves_do_not_belong_to_algeb.html
http://mathoverflow.net/questions/2314/several-topos-theory-questions related to the functor of points viewpoint and more
Any presheaf is a colimit of representables. Can you say filtered here??
<]]>- Sheaves of spectraWrite comment View comments
See of course also Jardine's notes
<]]>- Sheaves with transfersWrite comment View comments
Voevodsky: Homology of schemes I. Discusses the moral of the notion of transfers in the introduction. One of the points seem to be that CTs are functorial wrt correspondences iff they are ordinary, i.e. come from coeffs in a complex of abelian sheaves. Another point is that the "motive" of a CW complex should be its stable homotopy type, if we by motive mean universal wrt all CTs, but if we work with ordinary theories, it should be its singular simplicial complex, as an object in the derived cat of abelian groups. More details provided.
<]]>- ShimuraWrite comment View comments
Biography: The map of my life
Collected papers, at least 4 volumes.
<]]>- Shimura varietyWrite comment View comments
Folder: AG/Shimura varieties
See references in the L-function database
http://mathoverflow.net/questions/11219/what-is-a-good-roadmap-for-learning-shimura-curves
http://mathoverflow.net/questions/99341/book-on-shimura-varieties
http://mathoverflow.net/questions/77504/a-route-towards-understanding-shimura-varieties
http://mathoverflow.net/questions/14175/how-to-learn-about-shimura-varieties
http://mathoverflow.net/questions/75632/which-shimura-varieties-are-known-to-be-automorphic
Boutot et al: Varietes de Shimura et fonctions L. 1979. Good intro to many things, it seems. No electronic copy
arXiv:1206.6730 A remark on a conjecture of Buzzard-Gee and the cohomology of Shimura varieties from arXiv Front: math.NT by Christian Johansson We compare the conjecture of Buzzard-Gee on the association of Galois representations to C-algebraic automorphic representations with the conjectural description of the cohomology of Shimura varieties due to Kottwitz, and the reciprocity law at infinity due to Arthur. This is done by extending Langlands's representation of the L-group associated with a Shimura datum to a representation of the C-group of Buzzard-Gee. The approach offers an explanation of the explicit Tate twist appearing in Kottwitz's description.
<]]>- ShipleyWrite comment View comments
- <]]>
- ShtukasWrite comment View comments
A brief introduction is found in Pragacz ed, in folder AG/moduli.
<]]>- Siegel modular formWrite comment View comments
Andrianov: Intro to Siegel modular forms and Dir series, Universitext
Introductory Lectures on Siegel Modular Forms (Cambridge Studies in Advanced Mathematics) from Mathematics by: Helmut Klingen
<]]>- Simplicial categoryWrite comment View comments
See Goerss-Jardine chapter VIII for simplicial cats and simplicial functors. This has applications to homotopy coherence. "The main result of this chapter (due to Dwyer and Kan, Theorem 2.13 below) is a generalization of the assertion that simplicial functors of the form
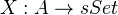 are equivalent to diagrams of the form
are equivalent to diagrams of the form 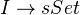 in the case where the simplicial category A is a resolution of the category I. "<]]>
in the case where the simplicial category A is a resolution of the category I. "<]]>- Simplicial commutative algebraWrite comment View comments
See Toen CRM 2008 notes, Chapter 4, in Toen web unpublished folder. In particular, he defines flat, smooth and etale morphisms.
http://mathoverflow.net/questions/94846/reference-request-cdga-vs-salg-in-char-0
<]]>- Simplicial complexWrite comment View comments
In MR743606, there is a notion of two abstract finite simplicial complexes being combinatorially equivalent; this happens iff they have isomorphic Cohen-Macauley rings.
<]]>- Simplicial groupWrite comment View comments
Jardine-Goerss chapter V treats simplicial groups and groupoids. For example, the category of sSets with an action of a simplicial group
 admits a model structure, and cofibrant objects correspond to principal
admits a model structure, and cofibrant objects correspond to principal  -fibrations.
-fibrations.There is an equivalence of homotopy cats (probably a Quillen equivalence) between simplicial groups and reduced simplicial sets. Similarly for simplicial groupoids and simplicial sets. See Jardine-Goerss V.6. They also describe Milnor's FK construction, a simplicial group being a fibrant model for
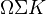 .<]]>
.<]]>- Simplicial homotopy theoryWrite comment View comments
nlab entries: simplicial homotopy group, horn, simplicial homotopy
There is a book by Jardine and Goerss with the above title. The book is also available online here, maybe slightly different from the published version.
We list the notions explained in the book for searchability. Alexander-Whitney map, almost free morphism, anodyne extension, barycentric subdivision, bisimplex, bisimplicial abelian group, bisimplicial set, bonding map, Bousfield factorization, Bousfield-Kan R-completion, Bousfield-Kan R-resolution, G-bundle, category translation, resolution of a category, classifying object, classifying space, closed n-loop, model structure (Reedy, Moerdijk, f-local, Q-structure, cofibrantly generated, stable, strict, towers), cocycle, codegeneracy, coface, coglueing lemma, cohomotopy groups, pointed cone, continuous functor, coskeleton, covering system, equivariant Dold-Kan correspondence, Dwyer-Kan theorem,
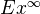 functor, Ext-p complete groups, Eilenberg subcomplex, Eilenberg-Zilber theorem, endpoint preserving, equivariant cohomology, expontial law, extension condition, external product, extra degeneracy, f-injective map, f-local space, f-localization, various kinds of fibration (Reedy, Serre, Q-fibration, acyclic, diagonal, global, minimal, pointwise, principal, stable, strict), Freudenthal suspension theorem, fringed spectral sequence, function complex, glueing lemma, Grothendieck construction, group completion, free groupoid, fundamental groupoid, homotopically full and faithful, homotopy cartesian, homotopy coherent diagram, homotopy colimit, homotopy fibre sequence, homotopy inverse limit, homotopy left Kan extension, homotopy pullback, homotopy spectral sequence (for a cosimplicial space, for a homotopy inverse limit, of a tower), horisontal normalization, horn, Hurewicz map, Hurewicz theorem, interchange law, join functor, k-invariant, Kan complex, Kan extension, Kan suspension, latching object, lax functor, left homotopy, local coefficient system, loop group, loop groupoid, loop spectrum, fake loop spectrum, loop space, matching object, matching space, Milnor FK-construction, Milnor exact sequence, Moore complex, Moore bicomplex, Moore-Postnikov section, Moore-Postnikov tower, nilpotent space, p-completion of a space, p-completion of an abelian group, Postnikov section, Postnikov tower, projective generator, pseudo cross-section, quasi-isomorphism, realization, n-reduced, relative homotopy group, retract, right lifting property, saturated, segment, Serre spectral sequence, shuffle map, simplical [abelian gruop, algebra, category, circle, coalgebra, functor, graded algebra, graded module, group, group action, groupoid, homotopy, map, model category, module, presheaf], simplicial set (n-fold, n-truncated, diagonal, reduced), singular set, skeleton, small object argument, spectrum, stable category, suspension ,Theorem B, total derived functor theorem, transgression, translation object, tree, trisimplicial set, universal cover, unstable algebra, van Kampen theorem, vertical path component, vertical simplicial set, weak equivalence, f-local equivalence, Q-weak equivalence, pointwise WE, Reedy WE, stable equivalence, strict WE of spectra, weak r-equivalence.
functor, Ext-p complete groups, Eilenberg subcomplex, Eilenberg-Zilber theorem, endpoint preserving, equivariant cohomology, expontial law, extension condition, external product, extra degeneracy, f-injective map, f-local space, f-localization, various kinds of fibration (Reedy, Serre, Q-fibration, acyclic, diagonal, global, minimal, pointwise, principal, stable, strict), Freudenthal suspension theorem, fringed spectral sequence, function complex, glueing lemma, Grothendieck construction, group completion, free groupoid, fundamental groupoid, homotopically full and faithful, homotopy cartesian, homotopy coherent diagram, homotopy colimit, homotopy fibre sequence, homotopy inverse limit, homotopy left Kan extension, homotopy pullback, homotopy spectral sequence (for a cosimplicial space, for a homotopy inverse limit, of a tower), horisontal normalization, horn, Hurewicz map, Hurewicz theorem, interchange law, join functor, k-invariant, Kan complex, Kan extension, Kan suspension, latching object, lax functor, left homotopy, local coefficient system, loop group, loop groupoid, loop spectrum, fake loop spectrum, loop space, matching object, matching space, Milnor FK-construction, Milnor exact sequence, Moore complex, Moore bicomplex, Moore-Postnikov section, Moore-Postnikov tower, nilpotent space, p-completion of a space, p-completion of an abelian group, Postnikov section, Postnikov tower, projective generator, pseudo cross-section, quasi-isomorphism, realization, n-reduced, relative homotopy group, retract, right lifting property, saturated, segment, Serre spectral sequence, shuffle map, simplical [abelian gruop, algebra, category, circle, coalgebra, functor, graded algebra, graded module, group, group action, groupoid, homotopy, map, model category, module, presheaf], simplicial set (n-fold, n-truncated, diagonal, reduced), singular set, skeleton, small object argument, spectrum, stable category, suspension ,Theorem B, total derived functor theorem, transgression, translation object, tree, trisimplicial set, universal cover, unstable algebra, van Kampen theorem, vertical path component, vertical simplicial set, weak equivalence, f-local equivalence, Q-weak equivalence, pointwise WE, Reedy WE, stable equivalence, strict WE of spectra, weak r-equivalence.
There is also an article by Curtis with this name, from 1971.
<]]>- Simplicial model categoryWrite comment View comments
See Module over a monoidal MC.
See also Dundas, page 42. Here the notions of tensored and cotensored are also defined.
Rezk, Schwede, Shipley: Simplicial Structures on Model Categories and Functors (2001). Abstract: We produce a highly structured way of associating a simplicial category to a model category which improves on work of Dwyer and Kan and answers a question of Hovey. We show that model categories satisfying a certain axiom are Quillen equivalent to simplicial model categories. A simplicial model category provides higher order structure such as composable mapping spaces and homotopy colimits. We also show that certain homotopy invariant functors can be replaced by weakly equivalent simplicial, or ...
<]]>- Simplicial objectWrite comment View comments
[CDATA[For skeleta, see Goerss-Jardine chapter VII.
Beatrice R Gonzalez on simplicial descent categories. Discusses homotopical structures on a category and on the category of simplicial objects in a category. http://front.math.ucdavis.edu/0808.3684
A simplicial object in a category
 is a functor
is a functor 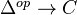 . A cosimplicial object is a functor
. A cosimplicial object is a functor 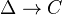 .
.Here
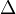 is the category of objects
is the category of objects 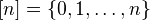 and morphisms the weakly order-preserving maps, i.e. maps
and morphisms the weakly order-preserving maps, i.e. maps  such that
such that 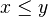 implies
implies 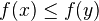 . Note that every such map can be factored uniquely as an injective map followed by a surjective map. The category
. Note that every such map can be factored uniquely as an injective map followed by a surjective map. The category 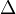 is generated by the injective maps
is generated by the injective maps 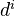 and the surjective maps
and the surjective maps 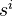 satisfying the cosimplicial identities.
satisfying the cosimplicial identities.A simplicial object is given by objects
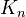 for each non-negative
for each non-negative  , together with face maps
, together with face maps 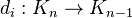 (
(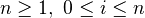 ) and degeneracy maps
) and degeneracy maps 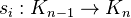 (
(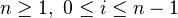 ), which must satisfy the simplicial identities:
), which must satisfy the simplicial identities:A map of simplicial objects is equivalent to a collection of maps
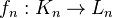 commuting with the face and degeneracy maps.
commuting with the face and degeneracy maps.
Notes from Goerss and Schemmerhorn: Description and handling of skeletons, using Kan extensions. One considers a complete and cocomplete category, and simplicial objects in this category. Latching and matching objects. Applications to lifting problems, by induction. When our category has enough colimits, have a notion of geometric realization from
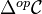 to
to 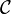 . If
. If  is a model category, this can be made into a Quillen functor. Description of the (Reedy?) model category structure on
is a model category, this can be made into a Quillen functor. Description of the (Reedy?) model category structure on 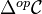 . If
. If  is cofibrant, then it is also cofibrant in the Reedy model structure. This is not true for fibrant. More details on this.<]]>
is cofibrant, then it is also cofibrant in the Reedy model structure. This is not true for fibrant. More details on this.<]]>- Simplicial presheavesWrite comment View comments
Simplicial presheaves and simplicial sheaves seem to play an important role in homotopy theory. For an introduction see Jardine's Fields lecture notes, or his longer notes
Toen Barcelona notes.
nLab on model structures, see also local model structure on simplicial presheaves
http://ncatlab.org/nlab/show/descent+for+simplicial+presheaves
Brillian and brief intro in Toen Essen talk, to stacks, simplicial presheaves with various model structures, and the conceptual difference between simplicial sheaves and presheaves. Also the key ideas on simplicial presheaves on a model site, i.e. taking into account a model structure on the base category.
Toen: Thm de RR pour les champs de DM. File Toen web publ rrchamp.pdf. Discusses K-theory and RR for DM stacks, but also various notions of descent, including basic stuff on simplicial presheaves, homological descent, and etale descent.
Lectures of Vaquie in HTAG09: Some notes: For any category, presheaves on it can be endowed with the (global) projective model structure. Also have the local proj model str, and we can view this as a Bousfield loc of the global one. Same result for injective instead of projective. The class S needed for the Bousfield loc is defined in terms of the notion of hypercover, and descent wrt a hypercover. Also local model str on simplicial presheaves on a model site. Universality statement for
 and functors from
and functors from  to a model cat, works for the projective (global) model structure only.
to a model cat, works for the projective (global) model structure only.http://mathoverflow.net/questions/9490/what-are-the-fibrant-objects-in-the-injective-model-structure
Some random notes
In K0129, Jardine proves that the categories of simplicial presheaves and simplicial sheaves on an arbitrary Grothendieck site have proper closed simplicial model structures.
In K0175 there is something about localization theories for simplicial presheaves.
Blander: In this note we introduce the local projective model structure on simplicial presheaves and as an application give a simplified proof of Voevodsky's comparison theorem, which asserts that the motivic stable homotopy categories in the Nisnevich and cdh topologies are equivalent.
There might be many interesting articles by Dugger and Isaksen, for example K0563
Flasque model structures for simplicial presheaves , by Daniel C. Isaksen K0676. This is an alternative to the projective and the injective model structures.
Consider the general setting of a category of functors from a category
 to
to  . We can define the projective model structure on this functor category as follows: WEs and fibrations are defined pointwise, while a cofibration is a "retract of a cellular inclusion" (see Dundas, p.40). Can define another model structure (page 41) in which WEs and cofibrations are defined pointwise. This is Quillen equivalent to the projective model structure (Heller).
. We can define the projective model structure on this functor category as follows: WEs and fibrations are defined pointwise, while a cofibration is a "retract of a cellular inclusion" (see Dundas, p.40). Can define another model structure (page 41) in which WEs and cofibrations are defined pointwise. This is Quillen equivalent to the projective model structure (Heller).Rezk: Fibrations and homotopy colimits of simplicial sheaves. Abstract: We show that homotopy pullbacks of sheaves of simplicial sets over a Grothendieck topology distribute over homotopy colimits; this generalizes a result of Puppe about topological spaces. In addition, we show that inverse image functors between categories of simplicial sheaves preserve homotopy pullback squares. The method we use introduces the notion of a sharp map, which is analogous to the notion of a quasi-fibration of spaces, and seems to be of independent interest.
C. Simpson. The topological realization of a simplicial presheaf, q-alg/9609004.
Feliu (thesis) reviews the homotopy theory of simplicial sheaves, in particular the Zariski site. Simplicial sheaves on a site form a simplicial model cat. Generalized cohomology theories defined with simplicial sheaves in both variables. Also generalised cohomology of a simplicial sheaf, with coeffs in an infinite loop spectrum.
Feliu, cont: Def of space "constructed from schemes". Any simplicial scheme gives rise to such a space, but not the other way around, ref to Huber and Wildeshaus.
Feliu, cont: A limit lemma which describes maps from K-theory to another cohomology theory. Maybe this could also be applied to for example maps from l-adic cohomology.
<]]>- Simplicial presheaves IIWrite comment View comments
http://ncatlab.org/nlab/show/%C4%8Cech+model+structure+on+simplicial+presheaves
http://nlab.mathforge.org/nlab/show/Universal+Homotopy+Theories
http://mathoverflow.net/questions/30140/how-many-model-categories-have-the-same-weak-equivalences
<]]>- Simplicial resolutionWrite comment View comments
- <]]>
- Simplicial ringWrite comment View comments
http://ncatlab.org/nlab/show/simplicial+ring
See section 2.1 of Rognes: Algebraic K-theory of topological K-theory link for some equivalences with other categories related to S-algebras.
<]]>- Simplicial schemeWrite comment View comments
Content moved to tex file
Some articles
- Teleman and Simpson: De Rham's theorem for
 -stacks.
-stacks. - Huber and Wildeshaus (something wrong with the link)
<]]>- Teleman and Simpson: De Rham's theorem for
- Simplicial setWrite comment View comments
Some content moved to Simplicial techiques
Dundas is also a good reference. See also Pointed simplicial set
Def of Kan fibration and other useful things at nLab
nLab also here and simplicial homotopy groups
Model structures from nLab
Simplicial group from nLab
arXiv:0809.4221 An elementary illustrated introduction to simplicial sets from arXiv Front: math.CT by Greg Friedman This is an expository introduction to simplicial sets and simplicial homotopy theory with particular focus on relating the combinatorial aspects of the theory to their geometric/topological origins. It is intended to be accessible to students familiar with just the fundamentals of algebraic topology.
<]]>- Simplicial sheavesWrite comment View comments
Model structures from nLab, see maybe also the entry on global model structure, and local model str, and also the links under Simplicial presheaves
arXiv:1109.5477 A Projective Model Structure on Pro Simplicial Sheaves, and the Relative Étale Homotopy Type from arXiv Front: math.AG by Ilan Barnea, Tomer M. Schlank In \cite{Isa}, Isaksen showed that a proper model category $\cC$, induces a model structure on the pro category $Pro(\cC)$. In this paper we generalize Isaksen's theorem to the case when $\cC$ possess a weaker structure, which we call a "weak fibration category". Namely, we show that if $\cC$ is a weak fibration category, that satisfies an extra condition, there is a naturally induced model structure on $Pro(\cC)$. We then apply our theorem to the case when $\cC$ is the weak fibration category of simplicial sheafs on a Grothendieck site, where both weak equivalences and fibrations are local as in \cite{Jar}. This gives a new model structure on the category of pro simplicial sheaves. Using this new model structure we give a definition of the étale homotopy type of Artin and Mazur \cite{AM}, as the result of applying a derived functor. Our definition actually gives as object in $Pro(\cS)$ and not just in $Pro(Ho(\cS))$ as in \cite{AM}. Our definition also extends naturally to a relative notion of the étale homotopy type, as considered for example in \cite{HaSc}.
Dwyer and Kan have a number of papers on diagrams of simplicial sets, see e.g. MR744846. In "Function complexes etc" MR705421, they show that there is a model structure on any functor cat with target ´sSet´. They also compute homotopy type of function complexes. Another potentially important paper is "Equivalences between homotopy theories of diagrams" where they give conditions on a functor for the induced map on simplicial presheaves to give an equivalence of homotopy theories.
Various things of Gillet - check all these for any motivational text on simplicial sheaves. Motivation for simplicial sheaves include various constructions for stacks and Q-varieties, for example Chow groups, K-theory of simplicial schemes, line bundles on stacks, and more. In "Filtrations on higher algebraic Kth" he uses the homotopy theory of simplicial objects in a topos.
http://mathoverflow.net/questions/5179/global-fibrations-of-simplicial-sheaves
arXiv:1009.2930 Classifying spaces and fibrations of simplicial sheaves from arXiv Front: math.AT by Matthias Wendt In this paper, we discuss the construction of classifying spaces of fibre sequences in model categories of simplicial sheaves. One construction proceeds via Brown representability and provides a classification in the pointed model category. The second construction is given by the classifying space of the monoid of homotopy self-equivalences of a simplicial sheaf and provides the unpointed classification.
<]]>- Simplicial techniques LINKSWrite comment View comments
nLab links
MO Questions
<]]>- SingularitiesWrite comment View comments
Folder: AG/Singularities and monodromy
Some volumes by Brasselet (ed)
Giraud: Etudes locale des singularites. 1971-1972. Course notes on lots of things related to resolution, in particular in char p.
Greuel et al: Introduction to Singularities and Deformations (Springer Monographs in Mathematics)
http://mathoverflow.net/questions/38237/singularities-of-space-curves-open-question-lists
Singularities folder under Geometry.
<]]>- SketchWrite comment View comments
http://www.ncatlab.org/nlab/show/sketch
http://www.abstractmath.org/Articles/Forms.htm
Some material can be found in the Elephant
http://mathoverflow.net/questions/82716/on-sketches-and-institutions
<]]>- Slice filtrationWrite comment View comments
Voevodsky's Nordfjordeid lecture - supernice (Voevodsky folder). Working over a field unfortunately. Basic constructions, of SH etc. Brief discussion of Thom spaces and homotopy purity. Cohomology theories: the motivic EM spectrum, KGL, MGL, claim that the notions of orientation and FGLs have direct analogs for P1-spectra. The slice filtration (great intro), update on Open problems paper. The zero-th slice of the unit spectrum is HZ, this is known for fields of char zero. Brief discussion of AHSS. Appendix on the Nisnevich topology, Nisnevich descent, and model structures.
Check writings by Voevodsky, Levine, Huber. Relation to coniveau stuff?
Slice filtration on motives and the Hodge conjecture, by Annette Huber
Open problems paper of Voevodsky
Voevodsky: Motives over simplicial schemes, contains some material. He says that Lemma 5.12 (p 22) about Homs between various truncations (vanishing etc) holds in the triang cat of motives but not in SH, and this is the major difference between the slice filtration in the two settings. A counterexample in the SH setting is the Hopf map, see p 22 for more. Probably this also affects the adjointness properties of the truncations.
arXiv:1002.0317 On the Functoriality of the Slice Filtration from arXiv Front: math.AT by Pablo Pelaez Let $k$ be a field with resolution of singularities, and $X$ a separated $k$-scheme of finite type with structure map $g$. We show that the slice filtration in the motivic stable homotopy category commutes with pullback along $g$. Restricting the field further to the case of characteristic zero, we are able to compute the slices of Weibel's homotopy invariant $K$-theory \cite{MR991991} extending the result of Levine \cite{MR2365658}, and also the zero slice of the sphere spectrum extending the result of Levine \cite{MR2365658} and Voevodsky \cite{MR2101286}. We also show that the zero slice of the sphere spectrum is a strict cofibrant ring spectrum $\mathbf{HZ}{X}^{\slicefilt}$ which is stable under pullback and that all the slices have a canonical structure of strict modules over $\mathbf{HZ}{X}^{\slicefilt}$. If we consider rational coefficents and assume that $X$ is geometrically unibranch then relying on the work of Cisinski and D{é}glise \cite{mixedmotives}, we get that the zero slice of the sphere spectrum is given by Voevodsky's rational motivic cohomology spectrum $\mathbf{HZ}_{X}\otimes \mathbb Q$ and that the slices have transfers. This proves several conjectures of Voevodsky \cite[conjectures 1, 7, 10, 11]{MR1977582}.
<]]>- Slope filtrationsWrite comment View comments
Yves Andre: Slope filtrations. In Confluentes Math.
<]]>- Small object argumentWrite comment View comments
A tool for constructing functorial factorizations in categories. See Hovey, Section 2.1.
Without explaining what the individual terms mean, the statement is as follows:
Theorem: Suppose
 is a category containing all small colimits, and
is a category containing all small colimits, and 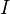 is a set of maps in
is a set of maps in  . Suppose the domains of the maps of
. Suppose the domains of the maps of 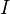 are small relative to
are small relative to 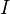 -cell. Then there is a functorial factorization
-cell. Then there is a functorial factorization 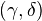 on
on  such that, for all morphisms
such that, for all morphisms  in
in  , the map
, the map 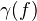 is in
is in 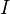 -cell and the map
-cell and the map 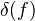 is in
is in 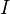 -inj.
-inj.See also Dundas, pp26.
Goerss and Schemmerhorn formulates it as follows: If a model category is cofibrantly generated, then factorizations can be chosen to be natural. The proof is also presented.
<]]>- Smash productWrite comment View comments
- <]]>
- SmoothWrite comment View comments
On smoothness of the affine line in derived AG, possibly related to positive/mixed characteristic problems: http://mathoverflow.net/questions/81187/can-a-common-mortal-understand-why-the-affine-line-is-not-smooth-in-brave-new-alg
http://ncatlab.org/nlab/show/smooth+infinity-stack
http://nlab.mathforge.org/nlab/show/smooth+algebra+in+algebraic+sense
http://ncatlab.org/nlab/show/homologically+smooth+dga
http://mathoverflow.net/questions/74570/formally-smooth-smooth
Something by Florian Marty?
http://mathoverflow.net/questions/20675/smooth-dg-algebras
http://mathoverflow.net/questions/107273/two-definitions-of-smoothness
<]]>- SoftwareWrite comment View comments
For making graphs, mind maps, diagrams, boxes
Grapviz (http://www.graphviz.org/Home.php) har jag hört ska vara bra men det är nog mera kod som genererar ett flödesschema än ett rita-och-dra program. Gratis så man kan ju pröva det.
Annars kanske ngn av dessa: http://shapesapp.com/
Kanske mindmap-program som Mindenode eller Xmind http://www.xmind.net/?
En enkel variant online: http://www.diagram.ly/ (liknar den funktion som finns i google docs och Neooffice/openoffice)
http://www.inspiration.com/ http://www.gliffy.com/ http://dia-installer.de/
Vet inte om ngn av dessa hanterar formler mm.
Eller Flow http://ctan.mackichan.com/support/flow/flowdoc.pdf
Omnigraffle?
<]]>- SouléWrite comment View comments
- <]]>
- SpaceWrite comment View comments
There are of course many different notions of "space" in mathematics. Here is a survey of Connes treating many of them.
http://www.ncatlab.org/nlab/show/space
http://golem.ph.utexas.edu/category/2010/10/cohesive_toposes.html
http://golem.ph.utexas.edu/category/2010/11/structures_in_a_cohesive_topos.html
nLab on space and quantity
http://ncatlab.org/nlab/show/infinity-space
http://ncatlab.org/nlab/show/%28infinity%2C1%29-quantity
http://ncatlab.org/nlab/show/structured+%28infinity%2C1%29-topos
For some approaches to generalized spaces in differential geometry, see the preface to Vassiliou: Geometry of Principal Sheaves, in Homol alg folder.
See n-category cafe for links to stuff about "generalized smooth spaces".
Compactly generated spaces: See Borceaux, vol 2 chapter 7.
Something by Grothendieck on categories as spaces: http://mathoverflow.net/questions/76505/in-which-situations-can-one-see-that-topological-spaces-are-ill-behaved-from-the
<]]>- Special values IIWrite comment View comments
arXiv:1209.5018 The $p$-adic Shintani cocycle from arXiv Front: math.NT by G. Ander Steele The Shintani cocycle on $\GL_n(\Q)$, as constructed by Hill, gives a cohomological interpretation of special values of zeta functions for totally real fields of degree $n$. We give an explicit criterion for a specialization of the Shintani cocycle to be $p$-adically interpolable. As a corollary, we recover the results of Deligne-Ribet, Cassou Noguès and Barsky on the construction of $p$-adic $L$-functions attached to totally real fields.
arXiv:1210.7460 Addendum to: Milne, Values of zeta functions of varieties over finite fields, Amer. J. Math. 108, (1986), 297-360 fra arXiv Front: math.AG av J. S. Milne The original article expressed the special values of the zeta function of a variety over a finite field in terms of the $\hat{Z}$-cohomology of the variety. As the article was being completed, Lichtenbaum conjectured the existence of certain motivic cohomology groups. Progress on his conjecture allows one to give a beautiful restatement of the main theorem of the article in terms of $Z$-cohomology groups.
<]]>- Special values of elliptic curvesWrite comment View comments
arXiv:1207.4722 Elliptic dilogarithms and parallel lines fra arXiv Front: math.NT av Anton Mellit We prove Boyd's conjectures relating Mahler's measures and values of L-functions of elliptic curves in the cases when the corresponding elliptic curve has conductor 14.
<]]>- Special values of L-functionsWrite comment View comments
A program for a conference on Tamagawa numbers
Stark's conjectures: recent work and new directions, Contemp. Math., 358, Amer. Math. Soc.
See everything by Lichtenbaum, including Motives volume. Also everything by de Jeu.
See Goncharov in K-theory handbook.
http://mathoverflow.net/questions/70217/k-theory-and-rings-of-integers
http://mathoverflow.net/questions/15153/periods-and-l-values
http://londonnumbertheory.wordpress.com/2010/01/15/zeros-and-poles/
Christophe Soulé, $K$-theory and values of zeta functions, in the mysterious Kuke Bass Pedrini 1997 volume that is nowhere to be found
Deligne: Valeurs de fonctions Let periodes d'integrales (1979)
Borel: Values of zeta functions at integers, cohomology and polylogarithms. 1994 survey, see things to scan for ref.
The cyclotomic trace map and values of zeta functions, by Thomas Geisser: K0697
MR544704 (81i:12010) 12A60 (12B20) Schneider, Peter U¨ ber gewisse Galoiscohomologiegruppen. (German) Math. Z. 168 (1979), no. 2, 181–205.
Nobushige Kurokawa, Special values of Selberg zeta functions (pp. 133--150) (1987)
MR1086888 (92g:11063) Bloch, Spencer(1-ILCC); Kato, Kazuya(J-TOKYO) $L$-functions and Tamagawa numbers of motives. The Grothendieck Festschrift, Vol. I, 333--400, Progr. Math., 86, Birkhäuser Boston, Boston, MA, 1990. See long MR review
Interesting: MR1330935 (96k:11083) de Shalit, Ehud(IL-HEBR-isomorphism) The explicit reciprocity law of Bloch-Kato. (English summary) Columbia University Number Theory Seminar (New York, 1992). Astérisque No. 228 (1995), 4, 197--221.
MR1408541 (97g:11136) Kolster, Manfred(3-MMAS); Nguyen Quang Do, Thong(F-FRAN-M); Fleckinger, Vincent(F-FRAN-M) Twisted $S$-units, $p$-adic class number formulas, and the Lichtenbaum conjectures. Duke Math. J. 84 (1996), no. 3, 679--717. (important paper)
MR1423032 (98a:11150) Ritter, Jürgen(D-AGSB-MI); Weiss, Alfred(3-AB) Cohomology of units and $L$-values at zero. The article under review presents quite significant progress on Stark's conjecture in the version of Tate. A considerable amount of algebraic machinery is developed to that end.
MR1609325 (99b:11051) Kings, Guido(D-MUNS) Higher regulators, Hilbert modular surfaces, and special values of $L$-functions. Duke Math. J. 92 (1998), no. 1, 61--127.
MR1685076 (2000b:11067) Huber, Annette(D-MUNS-isomorphism); Kings, Guido(D-MUNS-isomorphism) Dirichlet motives via modular curves. (English, French summary) Ann. Sci. École Norm. Sup. (4) 32 (1999), no. 3, 313--345.
MR1737227 (2001d:11071) Otsubo, Noriyuki(J-TOKYOGM) Note on conjectures of Beilinson-Bloch-Kato for cycle classes. (English summary) Manuscripta Math. 101 (2000), no. 1, 115--124.
MR1760901 (2001i:11082) Bloch, Spencer J.(1-CHI) Higher regulators, algebraic $K$-theory, and zeta functions of elliptic curves.
MR1817645 (2002k:11101) Kings, Guido(D-MUNS-isomorphism) The Tamagawa number conjecture for CM elliptic curves. Invent. Math. 143 (2001), no. 3, 571--627.
MR2002643 (2004m:11182) Huber, Annette(D-LEIP-isomorphism); Kings, Guido(D-RGBGNS1) Bloch-Kato conjecture and Main Conjecture of Iwasawa theory for Dirichlet characters.
MR2175640 (2006m:11168) Kolster, Manfred(3-MMAS) $K$-theory and arithmetic. (Summer school lectures on special values)
Soulein Asterisque 311: Genres de Todd et valeurs aux entiers des dérivées de fonctions $L$
arXiv:0909.0712 K_1 of products of Drinfeld modular curves and special values of L-functions from arXiv Front: math.AG by Ramesh Sreekantan Beilinson obtained a formula relating the special value of the L-function of H^2 of a product of modular curves to the regulator of an element of a motivic cohomology group - thus providing evidence for his general conjectures on special values of L-functions. In this paper we prove a similar formula for the L-function of the product of two Drinfeld modular curves providing evidence for an analogous conjecture in the case of function fields.
arXiv:0908.0171 Higher Mahler measures and zeta functions from arXiv Front: math.NT by Nobushige Kurokawa, Matilde Lalin, Hiroyuki Ochiai We consider a generalization of the Mahler measure of a multivariable polynomial $P$ as the integral of $\log^k|P|$ in the unit torus, as opposed to the classical definition with the integral of $\log|P|$. A zeta Mahler measure, involving the integral of $|P|^s$, is also considered. Specific examples are computed, yielding special values of zeta functions, Dirichlet $L$-functions, and polylogarithms.
arXiv:0908.0996 A cohomological Tamagawa number formula from arXiv Front: math.NT by Annette Huber, Guido Kings For smooth linear group schemes over $\bbZ$ we give a cohomological interpretation of the local Tamagawa measures as cohomological periods. This is in the spirit of the Tamagawa measures for motives defined by Bloch and Kato. We show that in the case of tori the cohomological and the motivic Tamagawa measures coincide, which reproves the Bloch-Kato conjecture for motives associated to tori.
http://mathoverflow.net/questions/13287/special-values-of-p-adic-l-functions
<]]>- Spectral sequenceWrite comment View comments
http://mathoverflow.net/questions/8052/why-are-spectral-sequences-so-ubiquitous
http://mathoverflow.net/questions/22188/introductory-book-on-spectral-sequences
Notes by Murfet
Hatcher Spectral Seqs book draft
http://ncatlab.org/nlab/show/spectral+sequence
References:
- Cartan and Eilenberg.
- Bott and Tu (el).
- Hilton and Stammbach
Probably also other things in the Homological algebra folder, including MacLane: Homology, and Gelfand-Manin: Methods.
Verdier has a notion of "spectral object". See Deligne: Décompositions dans... (Motives vol) for this. See also Deligne: Theoreme de Lefschetz et criteres de degenerescence de suites spectrales (1968, IHES)
Grayson (page 45 in K-theory handbook) has brief discussion on spectral seqs, for example those omig from a filtration on a spectrum. Read this again.
Gillet in K-theory handbook seems to be a very good starting point for a systematic treatment of spectral sequences
Weibel (p. 19) refers to Grothendieck's spectral sequence as a special case of the hypercohomology spectral sequence for the composition of two functors.
Some spectral sequences in algebraic geometry: Weight, Leray, local to global, hypercohomology, composition of two functors.
See List of spectral sequences
Deligne, P.: D´eg´en´erescence de suites spectrales et Th´eor`emes de Lefschetz.
Jardine, J.F.:The Leray spectral sequence. J. Pure Appl. Algebra 61, 189–196 (1989)
Segal, G.: Classifying spaces and spectral sequences. Publ. math. IHES 34, 105–112 (1968)
Maunder: The spectral sequence of an extraordinary cohomology theory (1963)
Check MacLane: Homology
Paranjape: Some spectral sequences for filtered complexes and applications (1996)
See also notes under Sheaf cohomology
McCleary book. In homology alg folder
Thomason article
Dwyer: Higher divided squares... "Every cosimplicial space gives rise to a spectral sequence. E.g. the Eilenberg-Moore spectral sequence. Study of operations on such spectral seqs."
Barakat on algorithm for computing with spectral sequence of a filtered cplx
LNM0134 treats the Eilenberb-Moore spectral sequence and interprets it as a Kunneth spectral sequence for a cohomology theory on an overcategory Top/B.
Pirashvili and Redondo: Cohomology of the Grothendieck construction, on arXiv. Treats a very general spectral sequence.
http://mathoverflow.net/questions/76337/exhaustiveness-and-regularness-of-a-filtration-of-a-complex
French on comparison between two spectral sequence for unstable homotopy groups (Adams and Goerss-Hopkins)
arXiv:1009.1125 The Goodwillie tower and the EHP sequence from arXiv Front: math.AT by Mark Behrens We study the interaction between the EHP sequence and the Goodwillie tower of the identity evaluated at spheres at the prime 2. Both give rise to spectral sequences (the EHP spectral sequence and the Goodwillie spectral sequence, respectively) which compute the unstable homotopy groups of spheres. We relate the Goodwillie filtration to the P map, and the Goodwillie differentials to the H map. Furthermore, we study an iterated Atiyah-Hirzebruch spectral sequence approach to the homotopy of the layers of the Goodwillie tower of the identity on spheres. We show that differentials in these spectral sequences give rise to differentials in the EHP spectral sequence. We use our theory to re-compute the 2-primary unstable stems through the Toda range (up to the 19-stem). We also study the homological behavior of the interaction between the EHP sequence and the Goodwillie tower of the identity. This homological analysis involves the introduction of Dyer-Lashof-like operations associated to M. Ching's operad structure on the derivatives of the identity. These operations act on the mod 2 stable homology of the Goodwillie layers of any functor from spaces to spaces.
Notes from Tohoku
Section 2.4
Consider an abelian cat
 . Def of filtered (decreasing) object in
. Def of filtered (decreasing) object in  , and morphism. Filtered objects form an additive cat. Def of associated graded, a covariant functor to graded objects.
, and morphism. Filtered objects form an additive cat. Def of associated graded, a covariant functor to graded objects.Def of spectral sequence in
 , as in Tamme. The cat of spectral sequences in
, as in Tamme. The cat of spectral sequences in  form an additive cat. Spectral functor, cohomological spectral sequence.
form an additive cat. Spectral functor, cohomological spectral sequence.Example: Let
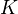 be a bicomplex in
be a bicomplex in  , with "finite diagonals". Then have two spectral sequences converging to the cohomology of the associated simple complex. For these the
, with "finite diagonals". Then have two spectral sequences converging to the cohomology of the associated simple complex. For these the 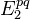 terms are defined by taking the
terms are defined by taking the 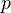 -th cohomology in one direction of the
-th cohomology in one direction of the 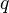 -th cohomology in the other direction.
-th cohomology in the other direction.Let
 be a covariant functor from one abelian cat
be a covariant functor from one abelian cat  to another
to another 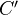 . Suppose the first cat has enough injectives. Let
. Suppose the first cat has enough injectives. Let 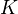 be a complex in
be a complex in  , bounded on the left. Then by Cartan-Eilenberg (Chap XVII) we can construct two spectral sequences
, bounded on the left. Then by Cartan-Eilenberg (Chap XVII) we can construct two spectral sequences 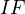 and
and 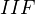 , bothe computing (what I think is) the derived functors of
, bothe computing (what I think is) the derived functors of  . This doesn't make any sense, probably I missed something here. He says that these sequences converge to "the hyperhomology functors of
. This doesn't make any sense, probably I missed something here. He says that these sequences converge to "the hyperhomology functors of  ", and they seem to use starting terms involving the derived functors. We recall the construction: Let
", and they seem to use starting terms involving the derived functors. We recall the construction: Let 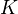 be concentrated in positive degrees. Take a double complex
be concentrated in positive degrees. Take a double complex 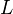 which in each degree is a resolution of
which in each degree is a resolution of 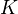 . Also, each node of
. Also, each node of 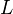 should be
should be  -acyclic (higher derived functors vanishing). Two ways of constructing such an
-acyclic (higher derived functors vanishing). Two ways of constructing such an 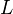 , including an explicit description of injective objects in the cat of complexes in
, including an explicit description of injective objects in the cat of complexes in  . More stuff about this hyperhomology, cannot decode the notation.
. More stuff about this hyperhomology, cannot decode the notation.Apparently the above machinery generates, as a special case, the usual Grothendieck spectral sequence theorem:
Thm: Let
 ,
, 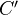 ,
, 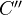 be three abelian cats, the first two having enough injectives. Let
be three abelian cats, the first two having enough injectives. Let 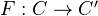 and
and 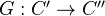 be covariant functors, such that
be covariant functors, such that  is left exact, and
is left exact, and  sends injectives to
sends injectives to  -acyclics. Then there exists a cohomological spectral functor on
-acyclics. Then there exists a cohomological spectral functor on  with values in
with values in 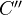 , with abutment the right derived functor of
, with abutment the right derived functor of 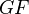 (convenablement filtre), with initial term
(convenablement filtre), with initial term 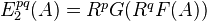 .
.Several remarks on this thm.
<]]>- Spectral sequence examplesWrite comment View comments
http://mathoverflow.net/questions/77071/generalized-beilinson-spectral-sequences
http://mathoverflow.net/questions/100591/galois-acting-on-l-adic-cohomology
http://mathoverflow.net/questions/32248/extraordinary-cohomology-as-a-derived-functor
Descent spectral sequence
http://mathoverflow.net/questions/74320/multiplicativity-in-the-descent-spectral-sequence
Leray spectral sequence
Local to global spectral sequence
Grothendieck spectral sequence
Goerss-Jardine IV.5. It is defined for any map
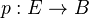 of simplicial sets, and converges to the homology of
of simplicial sets, and converges to the homology of 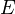 . If
. If 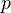 is a fibration we recover the Serre spectral sequence.
is a fibration we recover the Serre spectral sequence.Homotopy spectral sequence of a cosimplicial space
From Goerss-Jardine ch VII: One of the most commonly used tools in homotopy theory is the homotopy spectral sequence of a cosimplicial space. This first appeared in the work of Bousfield and Kan [14] and has been further analyzed by Bousfield [10]. Two of the standard examples include the Bousfield-Kan spectral sequence — an unstable Adams spectral sequence that arose before the general example [7] — and the spectral sequence for computing the homotopy groups of the homotopy inverse limit of a diagram of pointed spaces. One of the main purposes of this chapter is to define and discuss this kind of spectral sequence. We will do much more however; for example, we will give a detailed analysis of the total tower of a cosimplicial space, which is the basic object from which the spectral sequence is derived.
<]]>- Spectral sequence IIWrite comment View comments
arXiv:1210.7437 Higher order derived functors fra arXiv Front: math.CT av Hans-Joachim Baues, David Blanc We define a notion of higher derived functors, and show how these appear as the E^r term of many commonly used spectral sequences, including the (stable or unstable) Adams spectral sequence.
<]]>- Spectral sequences frameworksWrite comment View comments
A book by Grandis: http://www.worldscibooks.com/mathematics/8483.html
http://mathoverflow.net/questions/110812/what-kind-of-spectral-sequences-come-from-double-complexes
Spectral sequences on one blackboard: http://chromotopy.org/?p=721
Some things are in Freitag and Kiehl (short notation???)
arXiv:1007.0632 Homotopy spectral sequences from arXiv Front: math.CT by Marco Grandis In homotopy theory, exact sequences and spectral sequences consist of groups and pointed sets, linked by actions. We prove that the theory of such exact and spectral sequences can be established in a categorical setting which is based on the existence of kernels and cokernels with respect to an assigned ideal of null morphisms, a generalisation of abelian categories and Puppe-exact categories.
arXiv:1001.1556 A general framework for homotopic descent and codescent from arXiv Front: math.KT by Kathryn Hess In this paper we elaborate a general homotopy-theoretic framework in which to study problems of descent and completion and of their duals, codescent and cocompletion. Our approach to homotopic (co)descent and to derived (co)completion can be viewed as $\infty$-category-theoretic, as our framework is constructed in the universe of simplicially enriched categories, which are a model for $(\infty, 1)$-categories.
We provide general criteria, reminiscent of Mandell's theorem on $E_{\infty}$-algebra models of $p$-complete spaces, under which homotopic (co)descent is satisfied. Furthermore, we construct general descent and codescent spectral sequences, which we interpret in terms of derived (co)completion and homotopic (co)descent.We show that a number of very well-known spectral sequences, such as the unstable and stable Adams spectral sequences, the Adams-Novikov spectral sequence and the descent spectral sequence of a map, are examples of general (co)descent spectral sequences. There is also a close relationship between the Lichtenbaum-Quillen conjecture and homotopic descent along the Dwyer-Friedlander map from algebraic K-theory to étale K-theory. Moreover, there are intriguing analogies between derived cocompletion (respectively, completion) and homotopy left (respectively, right) Kan extensions and their associated assembly (respectively, coassembly) maps.<]]>- Spectral tripleWrite comment View comments
Morphisms of spectral triples can be viewed as KK-cycles with connection.
<]]>- SpectrumWrite comment View comments
n-Lab: In geometry, spectrum is a geometric space constructed from some data. Examples are Gelfand spectrum of a C *-algebra, Grothendieck spectrum of a commutative ring, formal spectrum of a complete noetherian commutative ring, primitive spectrum of a noncommutative (but unital) ring, left spectrum of a noncommutative ring, Rosenberg’s spectrum of an abelian category, Gabriel’s spectrum of indecomposable injectives, Pierce spectrum, Bercovich spectrum in rigid analytic geometry…
Distinguish from spectrum in the sense of homotopy theory.
http://nlab.mathforge.org/nlab/show/spectrum
http://www.ncatlab.org/nlab/show/combinatorial+spectrum
http://ncatlab.org/nlab/show/coordinate-free+spectrum
Tierney in LNM0087 has notes on the problem of inverting an endomorphism and adding directed colimits to a cat. Also a proof of the stable Dold-Kan correspondence, relating FD-spectra and unbounded chain complexes.
Ref: notes by Dundas. See also a blog post by Greg Muller and a survey article by Greenlees. Also the very brief appendix to Lichtenbaum: Motivic complexes. Maybe Whitehead: Recent advances in homotopy theory, and other older sources.
Let us write "space" for simplicial set.
In algebraic topology, a spectrum is a sequence of simplicial sets
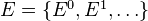 together with "structure" maps
together with "structure" maps 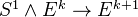 . A map of spectra is a sequence of maps
. A map of spectra is a sequence of maps 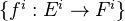 compatible with the structure maps. Get a category
compatible with the structure maps. Get a category  of spectra.
of spectra.Examples: Sphere spectrum, Eilenberg-MacLane spectrum (the 2nd is an
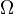 -spectrum).
-spectrum).An
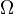 -spectrum is a spectrum for which the adjoint maps
-spectrum is a spectrum for which the adjoint maps 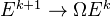 are homotopy equivalences. These spectra are the fibrant objects in the category of spectra.
are homotopy equivalences. These spectra are the fibrant objects in the category of spectra.Let
 be a simplicial set, and
be a simplicial set, and 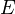 a spectrum. We define
a spectrum. We define 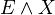 to be the spectrum
to be the spectrum 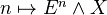 . We define
. We define 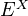 to be the spectrum
to be the spectrum 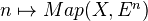 . Here
. Here 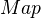 is the mapping space of pointed simplicial sets, see Simplicial set.
is the mapping space of pointed simplicial sets, see Simplicial set.The suspension spectrum functor from
 to
to  has a right adjoint, the zero'th space functor (sometimes called the underlying space). The term "underlying space" can also refer to the underlying infinite loop space,
has a right adjoint, the zero'th space functor (sometimes called the underlying space). The term "underlying space" can also refer to the underlying infinite loop space,  .
.We define the homotopy groups of a spectrum as
This defines a functor from spectra to graded abelian groups.
We say that a map of spectra is a stable equivalence if it induces an isomorphism on all homotopy groups. Inverting the stable equivalences produces the stable homotopy category. It is additive, and has a tensor product induced by the smash product.
Every cohomology theory is represented by a spectrum, and every spectrum represents a cohomology theory. This correspondence is given as follows: For a simplicial set
 , we define "homology"
, we define "homology" 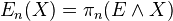 and "cohomology"
and "cohomology" 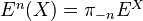 . In particular, taking the homology associated to sphere spectrum, we get the stable homotopy groups of
. In particular, taking the homology associated to sphere spectrum, we get the stable homotopy groups of  .
.We can define a model structure on spectra, by defining WEs and fibrations levelwise, and cofibrations by the lifting property. Dundas (page 43) calls this the pointwise model structure. Using the same cofibrations, and the stable equivalences, he defines a stable fibration to be a map with the RLP wrt all cofibrations which are stable equivalences. This gives the stable model structure on
 .
.Stuff from Adams
Lots of examples.
Subspectrum of a spectrum, relative homotopy groups, and a long exact sequence.
A lot more, see the summary of the book.
Brief summary of Jardine: Generalized étale cohomology theories
Chapter 1: Smash products of spectra. Defines spectra, cofibration, stable equivalence, stable cofibration. A spectrum is stably fibrant iff all its components are Kan complexes, such that each of the adjoint of the structure maps are weak equivalences. Construction of functorial smash product of two spectra.
A bispectrum can be interpreted as a spectrum object in the category of spectra. Such a thing is formed by the pointed simplicial sets
 , together with structure maps in "horizontal and vertical" direction. The problem is to extract a homotopy type from this. In Jardine, will work with Adams' original handicrafted smash product.
, together with structure maps in "horizontal and vertical" direction. The problem is to extract a homotopy type from this. In Jardine, will work with Adams' original handicrafted smash product.Def of fake suspention spectrum and fake loop spectrum of a spectrum
 . These are adjoint endofunctors of
. These are adjoint endofunctors of 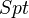 .
.Also define: n-fold spectrum, admissible function, admissible path, canonical path, canonical composite, diagonal spectrum, function complex, loop spectrum, loops space, partial spectrum,
 -spectrum.
-spectrum.Chapter 2: Abstract homotopy theory of n-fold spectra.
Intro: The category of n-fold spectra carries model structure both for the strict (i.e. levelwise) and the stable weak equivalences. The diagonal functor from n-fold spectra to spectra, induces an equivalence of homotopy categories. In other words, n-fold spectra is a model for the stable homotopy category. Analougously, the the stable homotopy categories arising from presheaves of spectra, and from presheaves of n-fold spectra, are equivalent. Keep in mind: The category of presheaves of spectra on a fixed site is not necessarily a model for the ordinary stable homotopy category. In fact, every Grothendieck topology gives rise to its own particular stable homotopy category. However, these theories are not unrelated. We will also show that the stable homotopy categories of presheaves of spectra carry a symmetric monoidal structure, with mult given by smash product, and unit given by the sphere spectrum.
Section 2.1 and 2.2: n-fold spectra, model structures, various compatibilities, equivalence of homotopy cats.
Section 2.3: Simplicial presheaves and pointed simplicial presheaves on a site. Model structures on these. Local WEs: in the presence of enough points these are defined by being WEs of simplicial sets on the stalks (otherwise, a condition on IMs of certain associated sheaves). Contrast: pointwise WE: each map of sections should be a WE of simplicial sets. Global fibration: lifting propery wrt cofibs which are local WEs. For two simplicial presheaves
 , have function complex
, have function complex  which is a simplicial set.
which is a simplicial set.Thm: These defs turn simplicical presheaves into a proper closed simplicial model category.
The category of presheaves of spectra (spectrum object in the category of pointed simplicial presheaves). Sheaf of stable homotopy groups for a presheaf of spectra. Various detail. Def: local stable equivalence of presheaves of spectra. Two defs of cofibs. Model structure.
Globally fibrant models, arise from Godement resolutions, can think of them as nonabelian versions of injective resolutions.
Note: The category of
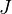 -diagrams in a Grothendieck topos is also a Grothendieck topos. Explicit construction.
-diagrams in a Grothendieck topos is also a Grothendieck topos. Explicit construction.Presheaves of n-fold spectra.
The homotopy category of presheaves of spectra (on a site) is a symmetric monoidal category under the smash product construction (compare Adams).
Chapter 3: First applications Function spectra (right adjoint to smashing on the left). Lots of details.
The abstract norm map for a group action on a spectrum. Also abstract transfer.
Chapter 4: Auxiliary results In the category of spectra, fiber sequences and cofiber sequences coincide.
Atiyah-Hirzebruch-Whitehead spectral sequence for the
 -homology
-homology 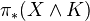 of a pointed simplicial set
of a pointed simplicial set 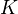 .
.Simplicial spectra and the spectral sequence for the stable homotopy groups of their associated diagonals.
Kan spectra and the equivalence of associated strict homotopy categories with the ordinary category of spectra.
Spectrum and Kan spectrum objects in the category of simplicial abelian groups, and the relation with the derived category for chain complexes of abelian groups. (Extension of the Dold-Kan corr.)
Postnikov towers for spectra.
Chapter 5: K-theory presheaves Smash prod pairings on K-theory spectra, cup products...
Construction of the K-theory presheaf of spectra, and its Waldhausen-style deloopings. Description of the smash product pairings of spectra which arise from bilinear maps of symmetric monoidal categories.
Much more...
Chapter 6: Generalized étale cohomology theories.
<]]>- Spectrum definitionsWrite comment View comments
Thomason: Symmetric monoidal categories model all connective spectra. Contains some background on spectra, connective spectra, E-infty spaces and infinite loop spaces.
A nice article of Strickland about Moore spectra and several other interesting things. http://front.math.ucdavis.edu/1205.2247
http://mathoverflow.net/questions/81740/modern-source-for-spectra-including-ring-spectra
<]]>- Spectrum IIWrite comment View comments
arXiv:1303.7108 A classification of small homotopy functors from spectra to spectra fra arXiv Front: math.AT av Boris Chorny We show that every small homotopy functor from spectra to spectra is weakly equivalent to a filtered colimit of representable functors represented in cofibrant spectra. Moreover, we present this classification as a Quillen equivalence of the category of small functors from spectra to spectra equipped with the homotopy model structure and the opposite of the pro-category of spectra with the strict model structure.
<]]>- Spectrum objectWrite comment View comments
http://nlab.mathforge.org/nlab/show/spectrum+object
About spectra and Brown rep:
http://mathoverflow.net/questions/117684/are-spectra-really-the-same-as-cohomology-theories
<]]>- SpitzweckWrite comment View comments
- <]]>
- Stability conditionsWrite comment View comments
Starting point: Maybe Bridgelands ICM address: Derived categories of coherent sheaves, and maybe also the papers Stability conditions on triangulated categories and Stability conditions on K3 surfaces
http://mathoverflow.net/questions/50513/stability-conditions-in-the-sense-of-kontsevich-soibelman
Huybrechts has an introductory article on arxiv.
<]]>- Stable homotopy categoryWrite comment View comments
Strickland notes: http://neil-strickland.staff.shef.ac.uk/research/stableintro.pdf
Lurie: Excellent course on stable homotopy theory: http://www.math.harvard.edu/~lurie/252x.html
Classically, the stable homotopy category is the homotopy category of the model category of spectra. Replacing spectra by symmetric spectra or S-modules give equivalent results.
Hovey, Palmieri and Strickland discusses axiomatic notions of stable homotopy categories. For more on this, see their original article, the discussion in Hovey's book, section 7.2, and also the article in Greenlees (ed): Axiomatic, Enriched and Motivic Homotopy Theory. A related MO link: http://mathoverflow.net/questions/98982/non-noetherian-stable-homotopy
To get a flavor of the axiomatics, Hovey defines an algebraic stable homotopy category as closed symmetric monoidal triangulated category together with a set of small strongly dualizable weak generators.
<]]>- Stable homotopy theoryWrite comment View comments
Some reference for stable homotopy theory in the sense of algebraic topology:
Basic
- A historical survey by May
- The blue book of Adams
- LNM0003 by Adams, looks very nice and easy to read
- See various things on the webpage of Strickland
- Many nice things are in these notes by Dundas
- D. Puppe, On the formal structure of stable homotopy theory, in Colloq. Alg. Topology, Aarhus University (1962), 65-71.
- LNM0165 Cohen 1970
- Various survey articles in Handbook of AT, in Alg Top folder
Advanced
- Ravenel: Nilpotence and Periodicity in Stable Homotopy Theory
- Morava: Towards a fundamental groupoid...
Some research articles
- http://front.math.ucdavis.edu/0907.0730 Symmetric powers in stable homotopy categories from arXiv Front: math.AG by Sergey Gorchinskiy, Vladimir Guletskii We construct Z-coefficient symmetric powers in a symmetric monoidal triangulated category, provided it is the homotopy category of a closed simplicial symmetric monoidal model category. Under certain natural assumptions, we show an existence of functorial towers for symmetric powers in distinguished triangles whose cones can be computed by Kuenneth's rule. Our theory is applicable to the topological and motivic stable homotopy categories through the idea of symmetric spectra. Some applications are presented and open questions are raised in both topological and motivic settings.
<]]>- Stable infinity-categoryWrite comment View comments
http://www.ncatlab.org/nlab/show/stable+(infinity,1)-category
http://www.ncatlab.org/nlab/show/Stable+Infinity-Categories
http://ncatlab.org/nlab/show/stable+%28infinity%2C1%29-topos the entry relates to sheaves of spectra
http://mathoverflow.net/questions/74386/how-should-i-think-of-the-infty-category-of-spectra
http://mathoverflow.net/questions/59270/is-the-infty-category-of-stable-infty-categories-stable
arXiv:1004.3087 Monoidal Infinity Category of Complexes from Tannakian Viewpoint from arXiv Front: math.AT by Hiroshi Fukuyama, Isamu Iwanari In this paper we prove that a morphism between schemes or stacks naturally corresponds to a symmetric monoidal functor between stable infinity-categories of quasi-coherent complexes. It can be viewed as a derived analogue of Tannaka duality. As a consequence, we deduce that an algebraic stack satisfying a certain condition can be recovered from the stable infinity-category of quasi-coherent complexes with tensor operation.
<]]>- Stable model categoryWrite comment View comments
http://www.ncatlab.org/nlab/show/stable+model+category
A stable model category is a pointed model category whose homotopy category is triangulated, meaning that the suspension functor is an equivalence.
Examples:
 , for R a commutative ring. Also
, for R a commutative ring. Also 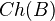 , for
, for  a commutative Hopf algebra over a field. S-modules. Symmetric spectra.
a commutative Hopf algebra over a field. S-modules. Symmetric spectra.Non-examples:
 and
and 
Can define closed monoidal triangulated category and show that the homotopy category of a stable monoidal model category is closed monoidal triangulated. See Hovey p. 178.
In a stable model category, homotopy pullback squares and homotopy pushout squares coincide.
arXiv:1204.5384 Stable left and right Bousfield localisations from arXiv Front: math.AT by David Barnes, Constanze Roitzheim We study left and right Bousfield localisations of stable model categories which preserve stability. This follows the lead of the two key examples: localisations of spectra with respect to a homology theory and A-torsion modules over a ring R with A a perfect R-algebra. We exploit stability to see that the resulting model structures are technically far better behaved than the general case. We can give explicit sets of generating cofibrations, show that these localisations preserve properness and give a complete characterisation of when they preserve monoidal structures. We apply these results to obtain convenient assumptions under which a stable model category is spectral. We then use Morita theory to gain an insight into the nature of right localisation and its homotopy category. We finish with a correspondence between left and right localisation.
<]]>- Stable motivic homotopy categoryWrite comment View comments
In Voevodsky (and Deligne): Lectures on cross functors, there is a discussion of the formalism of the four Grothendieck operations. This is maybe superseded by Ayoub's work. However, the lectures have some nice brief background info on the formalism (for etale sheaves), including PD and the four kind of (co)homology, indicating where there are difficulties. There is not really any material on motivic homotopy theory, it just says that such applications will be given "later".
Voevodsky's Nordfjordeid lecture - supernice (Voevodsky folder). Working over a field unfortunately. Basic constructions, of SH etc. Brief discussion of Thom spaces and homotopy purity. Cohomology theories: the motivic EM spectrum, KGL, MGL, claim that the notions of orientation and FGLs have direct analogs for P1-spectra. The slice filtration (great intro), update on Open problems paper. The zero-th slice of the unit spectrum is HZ, this is known for fields of char zero. Brief discussion of AHSS. Appendix on the Nisnevich topology, Nisnevich descent, and model structures.
<]]>- StackWrite comment View comments
Folder: AG/Stacks and algebraic spaces
See also Homotopical algebraic geometry and refs there.
Stacks: Book draft on Fulton's web page, probably more recent version on Kresch's page: http://www.math.uzh.ch/index.php?pr_vo_det&key1=1287&key2=580&no_cache=1
For some lectures and references, see Anel
Brillian and brief intro in Toen Essen talk, to stacks, simplicial presheaves with various model structures, and the conceptual difference between simplicial sheaves and presheaves.
A web-based algebraic stacks project
There are some references at Wikipedia.
Very basic definitions can be found in a chapter of Basic bundle theory etc, in K-theory folder.
A french book that looks really good is Laumon and Moret-Bailly
Good introduction in first chapter of FGA
Hollander: Classifying algebraic stacks
Teleman and Simpson: De Rham\\'s theorem for
-stacks.The command "\\" may only appear inside a "\begin ... \end" block\\\\inftyNotes by Giansiracusa on Orbifolds and stacks and algebraic spaces
One chapter in the notes of Mirkovic.
nlab algebraic stack
http://mathoverflow.net/questions/56962/what-about-stacks-of-categories-in-algebraic-geometry
http://ncatlab.org/nlab/show/derived+stack
http://www.ncatlab.org/nlab/show/infinity-stack
http://ncatlab.org/nlab/show/category+fibered+in+groupoids
Schapira introductory notes on sites, stacks etc. In Homol alg folder
Toen course, see folder cours under Toen web folder.
For the relation between higher stacks and the classical notion of stack, see Toen, file web unpubl msri2002.pdf.
Toen: Higher and derived stacks, a global overview. File web publ seatt.pdf. Also contains an intro to Segal cats, and some material on schematic homotopy types.
A summer school program:
Motivation: why stacks are needed. Basic example: moduli of curves of genus g. The 2-category of groupoids, schemes as functors, categories fibered in groupoids, pseudofunctors. The stack condition. Representable morphisms, definition of algebraic stack (in the sense of Deligne-Mumford). Quotient stacks, stacks associated to groupoids. The 2-category of stacks; open, closed substacks; topological space associated to a stack. Properties of stacks and of their morphisms; valuative criteria for separatedness and properness. Inertia stack. (Quasi)coherent sheaves on a stack, cohomology of sheaves. Main worked out examples: moduli of stable pointed curves, moduli of stable sheaves, weighted projective stacks and toric DM stacks. Infinitesimal study of moduli stacks and deformation theory. A short introduction to Artin stacks will also be provided.
Aim of Workshop. The Workshop is intended to discuss the state of the art in stacks and moduli theory. Up to now the following speakers have confirmed their participation: F. Catanese, G. Farkas, E. Sernesi, A. Verra, A. Vistoli.
http://mathematics.stackexchange.com/questions/727/algebraic-group-g-vs-algebraic-stack-bg
<]]>- StackificationWrite comment View comments
- <]]>
- Standard conjecturesWrite comment View comments
L. Clozel, ´ Equivalence num´erique et ´equivalence homologique pour les vari´et´es ab´eliennes sur les corps finis, Ann. Math. 150 (1999), 151–163. MR1715322
Harada preprints 2008
http://mathoverflow.net/questions/52248/questions-on-standard-motivic-conjectures
Lieberman: Numerical and homological equivalence of algebraic cycles on Hodge manifolds
Voevodsky: Nilpotence theorem for cycles algebraically equivalent to zero. Discusses smash nilpotence, the nilpotence conjectures, and various ideas related to mixed motives, theories of motivic type, the standard conjectures, and stuff about algebraic equivalence, for example mixed motives modulo alg equiv.
arXiv:1009.0413 The Standard Conjectures for holomorphic symplectic varieties deformation equivalent to Hilbert schemes of K3 surfaces from arXiv Front: math.AG by François Charles, Eyal Markman We prove the standard conjectures for complex projective varieties that are deformations of the Hilbert scheme of points on a K3 surface. The proof involves Verbitsky's theory of hyperholomorphic sheaves and a study of the cohomology algebra of Hilbert schemes of K3 surfaces.
<]]>- Stark conjectureWrite comment View comments
Snaith: Stark's conjectures and new Stickelberger phenomena. Contains an overview I think. CJM 58-2, one of the last articles.
IAS/PArk City proceedings from 2009. Should b the best intro.
<]]>- Steenrod algebraWrite comment View comments
H. R. Margolis, Spectra and the Steenrod algebra North-Holland Mathematical Library 29, North-Holland Publishing Co., Amsterdam, 1983.
For a construction and the characterization of Steenrod square, see the brief article of Culbertson in the Friedman scans folder.
Some original notes of Steenrod, see Steenrod.pdf in the Friedman scans folder.
Many articles in Geom. Topol. Monogr. 11 (2007), available online, I think all articles on arxiv.
LNM0168 The Steenrod algebra and its applications
Voevodsky comment during a talk in Muenster: Regarding the Morel-Hopkins iso. They probably prove it using the computation of the Steenrod alg, so restriction on char. I think it should be proven using geometric argument similar to Levine zero-slice paper. Then one could go the other way around, and use this iso to compute the Steenrod algebra without any char/torsion restrictions, e.g.
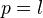 ok.
ok.http://mathoverflow.net/questions/55833/singular-complex-cohomology-ring-steenrod-operations
http://mathoverflow.net/questions/1094/commutativity-in-k-theory-and-cohomology
<]]>- SteinWrite comment View comments
- <]]>
- Stein manifoldWrite comment View comments
I think all the following is true, but it is just from my bad memory: A Stein manifold is defined by three properties, maybe analytically convex and two other things. It turns out that Stein manifolds are exactly the closed analytic submanifolds of
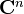 . Cartan's Theorem A and Theorem B are about coherent sheaves on Stein manifolds, and say that such a sheaf is generated by its global sections, and has vanishing higher cohomology.<]]>
. Cartan's Theorem A and Theorem B are about coherent sheaves on Stein manifolds, and say that such a sheaf is generated by its global sections, and has vanishing higher cohomology.<]]>- StricklandWrite comment View comments
- <]]>
- Structured spectraWrite comment View comments
arXiv:0908.1092 Diagram spaces, diagram spectra, and spectra of units from arXiv Front: math.AT by John Lind 1 person liked this We compare the infinite loop spaces associated to symmetric spectra, orthogonal spectra, and EKMM S-modules. Each of these categories of structured spectra has a corresponding category of structured spaces that receives the infinite loop space functor \Omega^\infty. We prove that these models for spaces are Quillen equivalent and that the infinite loop space functors \Omega^\infty agree. This comparison is then used to show that two different constructions of the spectrum of units gl_1 R of a structured ring spectrum R agree.
<]]>- Sullivan conjectureWrite comment View comments
- <]]>
- SupergeometryWrite comment View comments
- <]]>
- SupermanifoldWrite comment View comments
There is a definition in Gelfand and Manin: Methods of homology alg. See chapter 2 I think.
<]]>- SurgeryWrite comment View comments
There is some stuff (old but readable) in the Friedman scans folder, for example orlik.pdf.
Surgery folder
<]]>- SuslinWrite comment View comments
- <]]>
- SuspensionWrite comment View comments
A general setting in which a suspension functor exists is that of a pointed model category
http://ncatlab.org/nlab/show/reduced+suspension
http://nlab.mathforge.org/nlab/show/suspension+object
Note that there are two different suspension functors for a pointed sset: the smash product with
 and the Kan suspension
and the Kan suspension  . See Goerss-Jardine section III.5 and the summary paragraph at the start of chapter III.<]]>
. See Goerss-Jardine section III.5 and the summary paragraph at the start of chapter III.<]]>- SymbolsWrite comment View comments
Manin-Panchishkin chapter 4.
<]]>- Symmetric monoidal categoryWrite comment View comments
Def: A Monoidal category together with a commutativity isomorphism, satisfying four additional coherence diagrams. We can also define symmetric monoidal functor, and we get a 2-category.
Nice review in Thomason: Symmetric monoidal categories model all connective spectra. (Thomason folder)
Brief note by Baez
http://www.ncatlab.org/nlab/show/symmetric+monoidal+category
http://nlab.mathforge.org/nlab/show/symmetric+monoidal+%28infinity%2C1%29-category
<]]>- Symmetric spaceWrite comment View comments
Borel: Bourbaki exp 62 on hermitian symm spaces
http://mathoverflow.net/questions/76596/what-is-a-basic-textbook-to-studying-symmetric-spaces
Symmetric spaces folder
<]]>- Symmetric spectraWrite comment View comments
The original article, by Hovey, Shipley and Smith, is here.
Stefan Schwede has an interesting online book project
Jardine on presheaves of symmetric spectra: "This paper shows that there is a proper closed simplicial model category on the category of presheaves of symmetric spectra on an arbitrary Grothendieck site, and that the resulting homotopy category is equivalent to the stable category of presheaves of spectra."
Jardine on A1-local symmetric spectra: K0350. This article is replaced by Motivic symmetric spectra: "The paper demonstrates the existence of a theory of symmetric spectra for the motivic stable category. The main results imply the existence of a categorical model for the motivic stable category which has an internal symmetric monoidal smash product. More explicitly, it is shown that there is a proper closed simplicial model category structure for the category of symmetric T-spectra, suitably defined, on the smooth Nisnevich site of a noetherian scheme of finite type. The weak equivalences for this structure are stable equivalences, defined by analogy with the definitions given by Hovey, Shipley and Smith for ordinary symmetric spectra and by Jardine for presheaves of symmetric spectra, except that one suspends by the Morel-Voevodsky object T, and the underlying unstable category is the motivic closed model structure for simplicial presheaves on the Nisnevich site. The homotopy category obtained from the category of symmetric T-spectra is equivalent to the motivic stable category. "
Hovey on Spectra and symmetric spectra in general model categories
Sniggy gave a talk I think where he defined the model structure via an inclusion into a cat
 for a certain small cat
for a certain small cat  . Also a description of the symmetric monoidal structure in terms of a left Kan extension.
. Also a description of the symmetric monoidal structure in terms of a left Kan extension.arXiv:1108.3509 Positive model structures for abstract symmetric spectra from arXiv Front: math.AT by Sergey Gorchinskiy, Vladimir Guletskii We prove the existence of a suitable "positive" model structure for symmetric spectra over an abstract simplicial monoidal model category. This allows to generalize the theorem due to Elmendorf, Kriz, Mandell and May saying that the $n$-th symmetric power of a positively cofibrant topological spectrum is stably equivalent to the $n$-th homotopy symmetric power of that spectrum, see \cite{EKMM}, III, 5.1, and \cite{MMSS}, 15.5. As a consequence, we also prove the existence of left derive symmetric powers for abstract symmetric spectra. The results are general enough to be applicable to the Morel-Voevodsky's motivic symmetric spectra of schemes over a field.
<]]>- Symplectic stuffWrite comment View comments
Various articles of Kaledin might be interesting.
Appendix 4.7 of Felix, Oprea, Tanre in Homotopy th folder: Basic Hermitian and symplectic linear algebra, and basic notions of complex structures
Different faces of geometry, ed Donaldson, Eliashberg, Gromov. Contains some possibly useful survey articles.
http://sbseminar.wordpress.com/2012/01/09/what-is-a-symplectic-manifold-really/
http://sbseminar.wordpress.com/2012/01/14/why-do-symplectic-manifolds-need-to-be-closed/
Symplectic geometry: See various things in Symplectic folder
<]]>- Synthetic differential geometryWrite comment View comments
See Kock in Diff geom folder
Kock: Synthetic Geometry of Manifolds, in Geometry-Various folder.
Lavendhomme: Basic concepts of synthetic diff geom. In Geometry-Various folder.
http://mathoverflow.net/questions/55128/nice-application-of-generalized-smooth-spaces
<]]>- Syzygy moduleWrite comment View comments
Folder: AG/Syzygies
A basic notion of geometric invariant theory, see for example Eisenbud: Commutative algebra. Weibel mentions an analogy between homological algebra and stable homotopy theory, where syzygy modules correspond to loop spaces, and projective modules to contractible spaces.
<]]>