Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- t-structureWrite comment View comments
Ref: Beilinson-Bernstein-Deligne
Nakaoka: General heart construction on a triangulated category (I): unifying t-structures and cluster tilting subcategories. http://front.math.ucdavis.edu/0907.2080
http://mathoverflow.net/questions/32021/classification-of-t-structures-in-derived-category-of-r-mod
http://mathoverflow.net/questions/30536/t-structures-and-higher-categories
http://mathoverflow.net/questions/32615/applications-of-classifying-thick-subcategories
arXiv:0911.0343 Perverse coherent t-structures through torsion theories from arXiv Front: math.CT by Jorge Vitoria Bezrukavnikov (later together with Arinkin) recovered the work of Deligne defining perverse $t$-structures for the derived category of coherent sheaves on a projective variety. In this text we prove that these $t$-structures can be obtained through tilting torsion theories as in the work of Happel, Reiten and Smal\o. This approach proves to be slightly more general as it allows us to define, in the quasi-coherent setting, similar perverse $t$-structures for certain noncommutative projective planes.
arXiv:1009.5904 Weight structures and simple dg modules for positive dg algebras from arXiv Front: math.KT by Bernhard Keller, Pedro Nicolas Using techniques due to Dwyer-Greenlees-Iyengar we construct weight structures in triangulated categories generated by compact objects. We apply our result to show that, for a dg category whose homology vanishes in negative degrees and is semi-simple in degree 0, each simple module over the homology lifts to a dg module which is unique up to isomorphism in the derived category. This allows us, in certain situations, to deduce the existence of a canonical t-structure on the perfect derived category of a dg algebra. From this, we can obtain a bijection between hearts of t-structures and sets of so-called simple-minded objects for some dg algebras (including
arXiv:1206.4882 Glueing silting objects from arXiv Front: math.CT by Qunhua Liu, Jorge Vitoria, Dong Yang Recent results by Keller and Nicol{á}s and by Koenig and Yang have shown bijective correspondences between suitable classes of t-structures and co-t-structures with certain objects of the derived category: silting objects. On the other hand, the techniques of glueing (co-)t-structures along a recollement play an important role in the understanding of derived module categories. Using the above correspondence with silting objects we present explicit constructions of glueing of silting objects, and, furthermore, we answer the question of when is the glued silting tilting.
<]]>- Tamagawa numbersWrite comment View comments
See Weil: Adeles and algebraic groups. Deals with adelic points on algebraic varieties, and Tamagawa numbers of algebraic groups.
There is an article in PSPUM-9, in Algebraic groups folder.
http://mathoverflow.net/questions/96542/tamagawa-number-of-elliptic-curves-over-mathbbq
http://mathoverflow.net/questions/95050/geometric-explanation-of-tamagawa-numbers
http://mathoverflow.net/questions/44184/why-are-tamagawa-numbers-equal-to-pic-sha
http://mathoverflow.net/questions/96542/tamagawa-number-of-elliptic-curves-over-mathbbq
<]]>- Tame homotopy theoryWrite comment View comments
See paper by Dwyer with this name. Generalizes rational homotopy theory from 1-connected spaces to r-connected spaces.
<]]>- Tame ramificationWrite comment View comments
arXiv:0910.3812 Geometric criteria for tame ramification from arXiv Front: math.AG by Johannes Nicaise We prove an A'Campo type formula for the tame monodromy zeta function of a smooth and proper variety over a discretely valued field $K$. As a first application, we relate the orders of the tame monodromy eigenvalues on the $\ell$-adic cohomology of a $K$-curve to the geometry of a relatively minimal $sncd$-model, and we show that the semi-stable reduction theorem and Saito's criterion for cohomological tameness are immediate consequences of this result. As a second application, we compute the error term in the trace formula for smooth and proper $K$-varieties. We see that the validity of the trace formula would imply a partial generalization of Saito's criterion to arbitrary dimension.
<]]>- Tame symbolWrite comment View comments
Constructed by Tate. Takes two meromorphic functions on a Riemann surface and associates something at a point x. This satisfies a product formula. See Serre: Algebraic groups and classfields. Also generalizations by Deligne in IHES paper: Le symbole modere, 1991.
<]]>- Tannakian categoryWrite comment View comments
See Breen in the Motives volumes
Deligne: Categories tannakiennes (1990) in the Grothendieck Festschrift II.
Deligne and Milne: Tannakian categories (1982)
Saavedra Rivano: Categories tannakiennes. LNM 265, 1972.
Ref: Levine, page 26.
http://mathoverflow.net/questions/71660/why-would-the-category-of-motives-be-tannakian
Let
 be a field. A Tannakian category is a F-linear abelian tensor category which is rigid (i.e. has internal Homs) together with an exact faithful
be a field. A Tannakian category is a F-linear abelian tensor category which is rigid (i.e. has internal Homs) together with an exact faithful  -linear tensor functor to
-linear tensor functor to 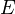 -mod for some field extension
-mod for some field extension 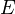 of
of  . A Tannakian category is neutral if we can take
. A Tannakian category is neutral if we can take 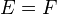 . Example of the latter: The category of finite-dimensional
. Example of the latter: The category of finite-dimensional  -reps of an affine group scheme
-reps of an affine group scheme  over
over  . If
. If  is neutral Tannakian with fiber functor
is neutral Tannakian with fiber functor 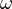 , then there is an affine group scheme
, then there is an affine group scheme  over
over  and a canonical isomorphism
and a canonical isomorphism 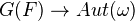 .
.
Notes from André:
Let
 be a field, let
be a field, let  be an abelian rigid tensor cat such that
be an abelian rigid tensor cat such that 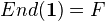 . A fiber functor on
. A fiber functor on  is an exact and faithful tensor functor
is an exact and faithful tensor functor 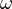 from
from  to finite-dimensional
to finite-dimensional 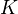 -vector spaces, where
-vector spaces, where 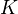 is some extension of
is some extension of  . If a fiber functor exists,
. If a fiber functor exists,  is called Tannakian. (If we can take
is called Tannakian. (If we can take 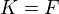 , then
, then  is called neutral Tannakian). For a Tannakian cat, one can define an affine
is called neutral Tannakian). For a Tannakian cat, one can define an affine 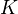 -group scheme
-group scheme 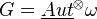 ; for every extension
; for every extension 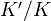 ,
, 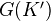 is the group of automorphisms of the tensor functor
is the group of automorphisms of the tensor functor 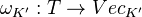 .
.Thm (Deligne): Let
 be a rigid tensor cat over a field
be a rigid tensor cat over a field  of characteristic zero, which is abelian and such that
of characteristic zero, which is abelian and such that 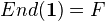 . Then
. Then  is Tannakian iff the rank of every object is a natural number iff for every object
is Tannakian iff the rank of every object is a natural number iff for every object 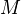 , sufficiently high exterior powers of
, sufficiently high exterior powers of 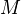 vanish.
vanish.For a neutral Tannakian category,
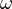 gives an equivalence of rigid tensor cats from
gives an equivalence of rigid tensor cats from  to
to 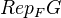 . Furthermore, the cat of fiber functors over
. Furthermore, the cat of fiber functors over  is equivalent to the cat (groupoid) of G-torsors (i.e. principal homogeneous
is equivalent to the cat (groupoid) of G-torsors (i.e. principal homogeneous  -spaces).
-spaces).We have a dictionary between properties of a group and properties of its Tannakian category:
 is an algebraic group (i.e. of finite type over
is an algebraic group (i.e. of finite type over  ) iff
) iff  admits a tensor generator., i.e. and object
admits a tensor generator., i.e. and object 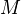 such that every object of
such that every object of  is a subquotient of some direct sums of tensor products of
is a subquotient of some direct sums of tensor products of 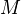 and its dual. In this case,
and its dual. In this case,  can be identified with a Zariski-closed algebraic subgroup of
can be identified with a Zariski-closed algebraic subgroup of 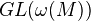 .
.- For
 of characteristic zero,
of characteristic zero,  is a pro-reductive group iff
is a pro-reductive group iff  is semisimple.
is semisimple.
Have a correspondence between tensor functors
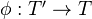 between neutral Tannakian cats, and homomorphisms
between neutral Tannakian cats, and homomorphisms 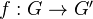 , induced by composition with the fiber functor. Under this correspondence:
, induced by composition with the fiber functor. Under this correspondence: is a monomorphism (closed immersion) iff every object
is a monomorphism (closed immersion) iff every object 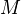 of
of  is a subquotient of an object in the image of
is a subquotient of an object in the image of 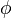
 is an epimorphism (faithfully flat) iff
is an epimorphism (faithfully flat) iff 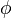 is fully faithful, and for every object
is fully faithful, and for every object 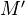 of
of 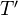 , every subobject of
, every subobject of 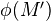 is the image under
is the image under 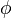 of a subobject of
of a subobject of 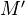 . (The last condition is automatic if
. (The last condition is automatic if  is semisimple.
is semisimple.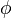 identifies
identifies 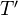 with the cat of objects of
with the cat of objects of  equipped with a
equipped with a 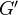 -action factorising the action of
-action factorising the action of  .
.
Note that without a given fiber functor, the group
 is not determined by
is not determined by  (example: inner forms). One can attach to every Tannakian cat
(example: inner forms). One can attach to every Tannakian cat  over
over  a commutative Hopf algebra in the cat of Ind-objects of
a commutative Hopf algebra in the cat of Ind-objects of  . Details of this.
. Details of this.Def of Tannakian subategory of a Tannakian cat.
<]]>- Tannakian dualityWrite comment View comments
Main idea: Giving a group is equivalent to giving its cat of representations. This can be made precised and also generalized.
http://nlab.mathforge.org/nlab/show/Tannaka+duality
Toen refers in the AIM talk to an unpublished homotopy version of Tannakian duality, in which schematic homotopy types appear as Tannakian dual of certain Tannakian model categories. He does give examples but no generalities.
Toen: Homotopical and higher categorical structures in algebraic geometry. File Toen web unpubl hab.pdf. Treats Tannakian duality for Segal cats, and schematic homotopy types.
An old preprint of Toen: Dualite de Tannaka superieure I. File Toen web unpubl tan.pdf.
arXiv:1204.5787 Tannaka duality over ring spectra from arXiv Front: math.AT by James Wallbridge We prove a Tannaka duality theorem for $(\infty,1)$-categories. This is a duality between certain derived group stacks, or more generally certain derived gerbes, and symmetric monoidal $(\infty,1)$-categories endowed with particular structure. This duality theorem is defined over commutative ring spectra and subsumes the classical statement. We show how the classical theory, and its extension over arbitrary rings, arises as a special case of our more general theory.
<]]>- TateWrite comment View comments
arXiv:1210.7459 The Work of John Tate fra arXiv Front: math.AG av J. S. Milne This is my article on Tate's work for the second volume in the book series on the Abel Prize winners. True to the epigraph, I have attempted to explain it in the context of the "great reformulation".
Selected publications:
- Symbols in arithmetic (1971)
<]]>- Tate conjectureWrite comment View comments
See survey in the Motives volumes.
http://mathoverflow.net/questions/73270/tate-conjecture-for-elliptic-curves-local-fields
An interesting article by Kahn
arXiv:1101.1730 On the generalised Tate conjecture for products of elliptic curves over finite fields from arXiv Front: math.AG by Bruno Kahn We prove the generalised Tate conjecture for H^3 of products of elliptic curves over finite fields, by slightly modifying an argument of M. Spiess concerning the Tate conjecture. We prove it fully if the elliptic curves run among at most 3 isogeny classes. We also show how things become more intricate from H^4 onwards, for more that 3 isogeny classes.
Andre: Cycles de Tate... proves something weaker (motivated cycles) for abelian varieties
arXiv:1206.4002 The Tate conjecture for K3 surfaces over finite fields from arXiv Front: math.AG by François Charles Artin's conjecture states that supersingular K3 surfaces over finite fields have Picard number 22. In this paper, we prove Artin's conjecture over fields of characteristic p>3. This implies Tate's conjecture for K3 surfaces over finite fields of characteristic p>3. Our results also yield the Tate conjecture for divisors on certain holomorphic symplectic varieties over finite fields, with some restrictions on the characteristic. As a consequence, we prove the Tate conjecture for cycles of codimension 2 on cubic fourfolds over finite fields of characteristic p>3.
<]]>- Tate-Poitou dualityWrite comment View comments
- <]]>
- Tate-Shafarevich conjectureWrite comment View comments
http://front.math.ucdavis.edu/0912.4325 Notes by Parshin and Zarhin on finiteness problems in arithmetic geometry. See also Manin-Panchiskin for good stuff on this.
<]]>- Tate-Shafarevich groupWrite comment View comments
http://mathoverflow.net/questions/19760/decomposition-of-tate-shafarevich-groups-in-field-extensions
http://mathoverflow.net/questions/9924/order-of-the-tate-shafarevich-group
arXiv:1108.6310 Counterexamples to the Hasse principle from arXiv Front: math.NT by Wayne Aitken, Franz Lemmermeyer In this article we develop counterexamples to the Hasse principle using only techniques from undergraduate number theory and algebra. By keeping the technical prerequisites to a minimum, we hope to provide a path for nonspecialists to this interesting area of number theory. The counterexamples considered here extend the classical counterexample of Lind and Reichardt. As discussed in an appendix, this type of counterexample is important in the theory of elliptic curves: today they are interpreted as nontrivial elements in the Tate--Shafarevich group.
arXiv:1108.3323 Local-global principles for torsors over arithmetic curves from arXiv Front: math.AG by David Harbater, Julia Hartmann, Daniel Krashen We consider local-global principles for torsors under linear algebraic groups, over function fields of curves over complete discretely valued fields. The obstruction to such a principle is a version of the Tate-Shafarevich group; and we show that it is finite in important cases. Moreover we obtain necessary and sufficient conditions for local-global principles to hold. The proofs use techniques from patching. We also give new applications to quadratic forms and central simple algebras.
<]]>- Tate-Thomason conjectureWrite comment View comments
arXiv:1007.0427 The Tate Thomason Conjecture from arXiv Front: math.AT by Marcelo Gomez Morteo We prove the Tate Thomason conjecture using K(l) localized spectra where K(1)=E(1)/l where l is an odd prime and E(1) is the complex topology spectrum. Fundamental to our proof is Theorem 2.1 below, where we show that certain K(1) localized spectra are E(1)^ module spectra.We also make fundamental use of the notion of etale and topological K Theory and its relation to algebraic K theory through Thomason's descent theorem.
<]]>- Tautological ringWrite comment View comments
arXiv:1101.2236 Relations in the tautological ring from arXiv Front: math.AG by R. Pandharipande, A. Pixton These notes cover our series of three lectures at Humboldt University in Berlin for the October 2010 conference "Intersection theory on moduli space" (organized by G. Farkas). The topic concerns relations among the kappa classes in the tautological ring of the moduli space of genus g curves. After a discussion of classical constructions in Wick form, we derive an explicit set of relations obtained from the virtual geometry of the moduli space of stable quotients. In a series of steps, the stable quotient relations are transformed to simpler and simpler forms. Our final result establishes a previously conjectural set of tautological relations proposed a decade ago by Faber-Zagier.
The Faber-Zagier relations are defined using g and a single series in one variable with coefficients (6i)!/(3i)!(2i)!. Whether these relations span the complete set of relations among the kappa classes on the moduli space of genus g curves is an interesting question.arXiv:1101.5489 Tautological and non-tautological cohomology of the moduli space of curves from arXiv Front: math.AG by C. Faber, R. Pandharipande After a short exposition of the basic properties of the tautological ring of the moduli space of genus g Deligne-Mumford stable curves with n markings, we explain three methods of detecting non-tautological classes in cohomology. The first is via curve counting over finite fields. The second is by obtaining length bounds on the action of the symmetric group S_n on tautological classes. The third is via classical boundary geometry. Several new non-tautological classes are found.
<]]>- Teichmuller theoryWrite comment View comments
Papadopoulos ed: Handbook of Teichm theory, at least 2 vols
<]]>- Tensor categoryWrite comment View comments
Ross and Street: The geometry of tensor calculus I. Gives an intro to tensor cats.
We consider (as motivation?) the category
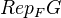 of finitedimensional representations over
of finitedimensional representations over  of an affine
of an affine  -group scheme
-group scheme  . The algebra of functions on
. The algebra of functions on  carries the structure of a "cogebra", actually a commutative Hopf algebra
carries the structure of a "cogebra", actually a commutative Hopf algebra 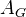 . The abelian
. The abelian  -linear category
-linear category  is equivalent to the category of comodules of finite
is equivalent to the category of comodules of finite  -dimension, relative to the cogebra structure of
-dimension, relative to the cogebra structure of  . The algebra structure of
. The algebra structure of 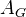 is hidden in the tensor structure of
is hidden in the tensor structure of 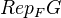 .
.Def: A tensor category over a commutative ring
 is an
is an  -linear cat with a tensor structure, i.e. a bilinear bifunctor, a unit object, and functorial isomorphisms expressing associativity, commutativity and unit laws; these are required to satisfy three coherence diagrams.
-linear cat with a tensor structure, i.e. a bilinear bifunctor, a unit object, and functorial isomorphisms expressing associativity, commutativity and unit laws; these are required to satisfy three coherence diagrams.A rigid tensor cat over
 is a tensor cat
is a tensor cat  over
over  equipped with a autoduality
equipped with a autoduality 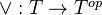 such that for every object
such that for every object 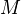 , tensoring on the right with the dual of
, tensoring on the right with the dual of 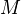 is left adjoint to tensoring on the right with
is left adjoint to tensoring on the right with 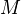 , and same with left and right interchanged.
, and same with left and right interchanged.This structure gives us adjunciton morphisms
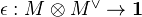 and
and 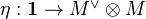 , called evaluation and coevaluation, satisfying certain properties. In a rigid tensor category, every endomorphism has a trace, which is element
, called evaluation and coevaluation, satisfying certain properties. In a rigid tensor category, every endomorphism has a trace, which is element 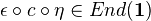 . We define the rank (or dimension) of an object
. We define the rank (or dimension) of an object 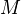 to be the trace of
to be the trace of 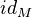 .
.Example: The cat of finitedimensional linear reps of a group, over some field? The unit object is the trivial rep, and rank is the obvious thing.
Example: The cat of
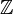 -graded finite-dimensional
-graded finite-dimensional 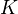 -vector spaces. Alternatively,
-vector spaces. Alternatively, 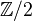 -graded. Tensor product turns this into a rigid tensor cat, in which the commutativity constraint is given be the Koszul sign rule. The rank of an object is its super-dimension
-graded. Tensor product turns this into a rigid tensor cat, in which the commutativity constraint is given be the Koszul sign rule. The rank of an object is its super-dimension 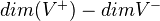 , where
, where 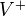 is the direct sum of the even parts etc.
is the direct sum of the even parts etc.Example: Combining the last two examples, one obtains the rigid tensor category of super-representations of
 . In practice, one considers often a certain subcat of this.
. In practice, one considers often a certain subcat of this.Example: The cat of vector bundles on a fixed
 -scheme. It has
-scheme. It has 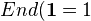 if proper and geometrically connected. The rank is what you think it is.
if proper and geometrically connected. The rank is what you think it is.Remark: In a pseudo-abelian rigid tensor category over a field
 of char 0, one can define the symmetric and exterior powers of any object
of char 0, one can define the symmetric and exterior powers of any object 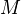 .
.Def: Tensor functor between tensor categories. (What you think it is).
If the tensor cats are rigids, any tensor functor between them is automatically compatible with taking duals, up to a natural isomorphism. Furthermore, because of duality, every morphism of tensor functors is an isomorphism.
Ezample: The free rigid tensor category on an object
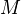 .<]]>
.<]]>- Test categoryWrite comment View comments
Some examples at nlab Nerve
See notes on my blog from Maltsiniotis talk at IHES
http://www.ncatlab.org/nlab/show/test+category
http://mathoverflow.net/questions/11045/are-non-empty-finite-sets-a-grothendieck-test-category
<]]>- Theta functionsWrite comment View comments
Folder: AG/Theta functions (many nice things)
Weil: Bourbaki exp 16
Ask Irene for other references if needed
Conference volume: Theta functions, Bowdoin 1987, Proc Symp Pure Math 49, maybe this is part I only.
A key author might be Barsotti. E.g. in Asterisque 63: Theta functions in positive char.
Review of Faltings: The determinant of cohomology in the etale topology Theta functions can be viewed as the canonical section of the determinant of cohomology. The corresponding notion in the etale topology would be L-series. "All known constructions of p-adic L-functions seem to be related to some situation where some etale cohomology has vanishing Euler char.
Theta functions: Last chapter of Shimura: Abelian Varieties with CM
<]]>- Thom spectraWrite comment View comments
arXiv:1006.4347 Topological Hochschild Homology of $K/p$ as a $Kp^\wedge$ module from arXiv Front: math.AT by Samik Basu Let $R$ be an $E\infty$-ring spectrum. Given a map $\zeta$ from a space $X$ to $BGL1R$, one can construct a Thom spectrum, $X^\zeta$, which generalises the classical notion of Thom spectrum for spherical fibrations in the case $R=S^0$, the sphere spectrum. If $X$ is a loop space ($\simeq \Omega Y$) and $\zeta$ is homotopy equivalent to $\Omega f$ for a map $f$ from $Y$ to $B^2GL1R$, then the Thom spectrum has an $A\infty$-ring structure. The Topological Hochschild Homology of these $A\infty$-ring spectra is equivalent to the Thom spectrum of a map out of the free loop space of $Y$.
This paper considers the case $X=S^1$, $R=Kp^\wedge$, the p-adic $K$-theory spectrum, and $\zeta = 1-p \in \pi1BGL1Kp^\wedge$. The associated Thom spectrum $(S^1)^\zeta$ is equivalent to the mod p $K$-theory spectrum $K/p$. The map $\zeta$ is homotopy equivalent to a loop map, so the Thom spectrum has an $A\infty$-ring structure. I will compute $\pi*THH^{K_p^\wedge}(K/p)$ using its description as a Thom spectrum.<]]>- ThomasonWrite comment View comments
For an overview of the work of Thomason, see K0104.
Some publications:
- Thomason: Homotopy colimits in the category of small categories.
- Thomason-Trobaugh
<]]>- Thomason model categoryWrite comment View comments
See Weibel's Thomason obituary for some details.
<]]>- ToenWrite comment View comments
Algebraic Geometry over model categories (a general approach to derived algebraic geometry), by Bertrand Toen and Gabriele Vezzosi: K0520
K0579: Homotopical Algebraic Geometry I Topos theory, by Bertrand Toen and Gabriele Vezzosi
An interesting conference, with some interesting names:
CATS3 is the third part of a series of conferences devoted to higher categorical structures in algebraic geometry. The meeting is intended to bring together experts in various subjects related to higher categorical and homotopical techniques in the context of algebraic geometry, as well as mathematicians from other fields who desire to learn about the recent advances in this area. The subjects covered by the conference will include: foundations of the theory of higher categories and homotopical algebra, stacks and higher stacks, derived and dg-categories, strong homotopy algebras, non-commutative geometry, derived deformation theory and derived algebraic geometry, non-abelian Hodge theory, string topology and string theory, CY-categories and homological mirror symmetry.
SPEAKERS: M. Anel, R. Bezrukavnikov, K. Costello, D. Fiorenza, D. Gaitsgory, A. Joyal, D. Kaledin, L. Katzarkov, J. Kock, M. Kontsevich, T. Leinster, J. Pridham, J. Morava, D. Spivak, G. Tabuada, M. Van den Bergh, M. Vaquie.
ORGANIZING COMMITTEE: Tony Pantev tpantev@math.upenn.edu Carlos Simpson carlos@unice.fr Bertrand Toen toen@picard.ups-tlse.fr Gabriele Vezzosi gabriele.vezzosi@gmail.com
<]]>- Topological algebraic geometryWrite comment View comments
In the Homotopy theory folder, see Goerss Copenhagen lectures (prereqs + slides). Synopsis: I would like to give a concise introduction to derived algebraic geometry over the moduli stack of formal groups. Put another way, I would like to discuss when continuous families of Landweber exact homology the- ories can be lifted to families of structured ring spectra. I would also like to explain why we care: this is part of long standing program (going back to Morava and others) of using arithmetic algebraic geometry to understand phenomena in stable homotopy theory. While very much a developing the- ory, the work of Hopkins, Miller, Lurie, Behrens, Lawson, and others over the last ten or so years have given us very precise tools. The theory and practice of these tools is the emphasis of these lectures. Topics we be a subset of the following list, depending on time and the background of the audience.
<]]>- Topological LanglandsWrite comment View comments
See Salch on arxiv, and his webpage
Various material (from the above seminar I think) in folder AG/Top Langlands
http://mathoverflow.net/questions/7283/topological-langlands
A talk abstract: Andrew Salch (Johns Hopkins University). A computational motivation for topological Langlands correspondences. Abstract: We describe the most effective known method for computing the stable homotopy groups of spheres at odd primes; this uses formal modules over p-adic number rings, together with base-change properties of the "chromatic filtration," i.e., local cohomology on the moduli stacks of formal modules, to construct the Adams-Novikov E_2-term. A consequence of these methods is the appearance of denominators of special values of Artin L-functions in the orders of the stable homotopy groups of spheres. We describe the role this phenomenon plays in motivating the (still very speculative) study of topological Langlands correspondences.
http://www.math.jhu.edu/~asalch/toplang/tltalk.pdf Talk of Salch
http://www.math.jhu.edu/~asalch/toplang/dca1.pdf Derived Carayol attack
<]]>- ToposWrite comment View comments
Some standard references are in folder AG/Topos theory
Many more references on Wikipedia
Caramello: The unification of Mathematics via Topos Theory (see also other things by Caramello on her webpage)
Joyal and Moerdijk: Toposes are Cohomologically Equivalent to Spaces (1990)
nLab quasi-topos
http://www.ncatlab.org/nlab/show/cosmos
nLab list of entries related to topos theory
http://www.ncatlab.org/nlab/show/classifying+topos
http://ncatlab.org/nlab/show/natural+numbers+object
http://ncatlab.org/nlab/show/Sheaves+in+Geometry+and+Logic
http://www.ncatlab.org/nlab/show/geometric+morphism
Toposes Triples Theories, by Barr and Wells, in Homol alg folder
Borceux vol 3 maybe.
<]]>- Toric topologyWrite comment View comments
arXiv:1102.1079 Toric Topology. Chapter 1: Geometry and combinatorics of polytopes from arXiv Front: math.AT by Victor Buchstaber, Taras Panov This is the first chapter in our "Toric Topology" book project. Further chapters are coming. Comments and suggestions are very welcome.
[arXiv:1210.2368] Toric Topology fra arXiv Front: math.AT av Victor Buchstaber, Taras Panov This is a preliminary version of our "Toric Topology" book project. Currently Chapters 1-5 and Appendices A,B,E,F are available. Further chapters are coming. Comments and suggestions are very welcome.
<]]>- Toric varietiesWrite comment View comments
Some stuff in folder AG/Toric varieties
Book by Fulton
Several chapters in Miller-Sturmfels: Combinatorial commutative algebra. In Comm alg folder.
Toronto talk by Burgos Gil
Morelli: Articles on K-theory and Todd class
For computational toric geometry, see people associated with this conference
Strickland thought on toric top
Toric varieties: Several papers by Cox, including "Recent developments in toric geometry" in Santa Cruz 1995 volume.
[arXiv:0911.3607] The functor of toric varieties associated with Weyl chambers and Losev-Manin moduli spaces from arXiv Front: math.AG by Victor Batyrev, Mark Blume A root system $R$ of rank $n$ defines an $n$-dimensional smooth projective toric variety $X(R)$ associated with its fan of Weyl chambers. We give a simple description of the functor of $X(R)$ in terms of the root system $R$ and apply this result in the case of root systems of type $A$ to give a new proof of the fact that the toric variety $X(An)$ is the fine moduli space $\bar{L}{n+1}$ of stable $(n+1)$-pointed chains of projective lines investigated by Losev and Manin.
arXiv:1102.5760 The Geometry of T-Varieties from arXiv Front: math.AG by Klaus Altmann, Nathan Owen Ilten, Lars Petersen, Hendrik Süß, Robert Vollmert This is a survey of the language of polyhedral divisors describing T-varieties. This language is explained in parallel to the well established theory of toric varieties. In addition to basic constructions, subjects touched on include singularities, separatedness and properness, divisors and intersection theory, cohomology, Cox rings, polarizations, and equivariant deformations, among others.
<]]>- Torsion in cohomologyWrite comment View comments
- <]]>
- Torsion in differential geometryWrite comment View comments
[CDATA[Mueller: Analytic torsion and R torsion of Riemannian manifolds. Adv Math 1978.
Ray and Singer: R-torsion and the Laplacian on Riemannian mfds. Adv Math 1971
http://ncatlab.org/nlab/show/torsion mentions several notions of torsion.
http://mathoverflow.net/questions/20493/what-is-torsion-in-differential-geometry-intuitively
http://mathoverflow.net/questions/58471/analytic-torsion-in-the-derived-category
arXiv:1406.3705 Lecture notes on torsions (Pavel Mnev)
<]]>- TorsorWrite comment View comments
See Toen course in cours folder under Toen, chapter 7.
[arXiv:0912.4551] Torsors, herds and flocks from arXiv Front: math.CT by Thomas Booker, Ross Street 1 person liked this This paper presents non-commutative and structural notions of torsor. The two are related by the machinery of Tannaka-Krein duality.
<]]>- Total derived functorWrite comment View comments
Let
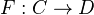 be a left Quillen functor. Define its total (left) derived functor
be a left Quillen functor. Define its total (left) derived functor 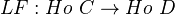 as the composite of
as the composite of 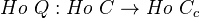
and
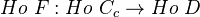
Here
 is the cofibrant replacement functor.
is the cofibrant replacement functor.Given a natural transformation
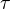 of left Quillen functors, define the total derived natural transformation
of left Quillen functors, define the total derived natural transformation 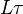 to be
to be 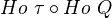 .
.Similarly, for a right Quillen functor we define the total (right) derived functor to be
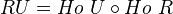
Consider the 2-category of model cats, left (resp. right) Quillen functors, and natural transformations. The triple: Homotopy category, total derived functor, and total derived natural transformation, define a pseudo-2-functor from this 2-category to the 2-category of categories. SImilar statement with Quillen adjunctions instead of Quillen functor.
Remark: One can define total derived functors in more general settings, I think. For example, Quillen describes the total left derived functor as a Kan extension.
Goerss-Jardine p 122: Quillen's total derived functor thm, explains when adjoint functors between model cats induces adjoint functors on the homotopy cats. The total left derived functor here is defined for functors from a simplicial model cat to any cat, sending WEs between cofibrant objects to isomorphisms. A version of the theorem is: For an adjoint pair (F, G) between simplicial model cats, the conclusion is true of
 preserves WEs between cofibrant objects and
preserves WEs between cofibrant objects and  WEs between fibrant objects. There are also some corollaries and variations on this theme.
WEs between fibrant objects. There are also some corollaries and variations on this theme.In Goerss and Schemmerhorn, page 17, there is a brief description of the spectral sequence total left derived functor of tensor product.
<]]>- Total spaceWrite comment View comments
LNM304 pp17 defines the total space of a cosimplicial space.
<]]>- TotaroWrite comment View comments
- <]]>
- TQFTWrite comment View comments
Topological Quantum Field Theory.
Functional analysis on the eve of the 21st century Contains article by Kapranov: Analogies between the Langlands Correspondence and Topological QFT. Really cool article. Follow-up here at MO.
http://mathoverflow.net/questions/359/a-reading-list-for-topological-quantum-field-theory
http://nlab.mathforge.org/nlab/show/extended+topological+quantum+field+theory
nLab on the cobordism hypothesis
http://nlab.mathforge.org/nlab/show/On+the+Classification+of+Topological+Field+Theories
http://nlab.mathforge.org/nlab/show/generalized+tangle+hypothesis
Some notes by May
A blog entry of Baez
Notes by Toen on higher-categorical structures in TQFT, in Toen web unpubl folder, etqft.dvi.
Blog post on Ben-Zvi lectures on Topological field theories
Lectures on tensor cats and modular functor. Link
Explore nlab stuff on Chern-Simons theory.
arXiv:1108.3349 A higher category of cobordisms and topological quantum field theory from arXiv Front: math.CT by Mark Feshbach, Alexander A. Voronov 1 person liked this The goal of this work is to describe a categorical formalism for (Extended) Topological Quantum Field Theories (TQFTs) and present them as functors from a suitable category of cobordisms with corners to a linear category, generalizing 2d open-closed TQFTs to higher dimensions. The approach is based on the notion of an n-fold category by C. Ehresmann, weakened in the spirit of monoidal categories (associators, interchangers, Mac Lane's pentagons and hexagons), in contrast with the simplicial (weak Kan and complete Segal) approach of Jacob Lurie. We show how different Topological Quantum Field Theories, such as gauge, Chern-Simons, Yang-Mills, WZW, Seiberg-Witten, Rozansky-Witten, and AKSZ theories, as well as sigma model, may be described as functors from the pseudo n-fold category of cobordisms to a pseudo n-fold category of sets.
<]]>- TraceWrite comment View comments
http://ncatlab.org/nlab/show/Dennis+trace
For trace methods related to K-theory and Hochschild homology, Dennis trace map etc, see Madsen ICM talk.
http://front.math.ucdavis.edu/1101.1883 Grothendieck's trace map for arithmetic surfaces via residues and higher adeles from arXiv Front: math.AG by Matthew Morrow We establish the reciprocity law along a vertical curve for residues of differential forms on arithmetic surfaces, and describe Grothendieck's trace map of the surface as a sum of residues.
<]]>- Track categoryWrite comment View comments
arXiv:1108.3376 Higher order derived functors and the Adams spectral sequence from arXiv Front: math.CT by Hans-Joachim Baues, David Blanc Classical homological algebra considers chain complexes, resolutions, and derived functors in additive categories. We describe track algebras in dimension n, which generalize additive categories, and we define higher order chain complexes, resolutions, and derived functors. We show that higher order resolutions exist in higher track categories, and that they determine higher order Ext-groups. In particular, the E_m-term of the Adams spectral sequence (m less than n+3) is a higher order Ext-group, which is determined by the track algebra of higher cohomology operations.
<]]>- Transfinite stuffWrite comment View comments
- <]]>
- Triangulated categoryWrite comment View comments
Gelfand-Manin: Algebra V. Good chapter with examples!
Gelfand and Manin: Methods book
Neeman book!
See notes by Murfet: Part I, Part II and Part III
Most triangulated cats in nature appear as the homotopy category of a stable model category. For an example where this is not the case, see Muro, with an improvement here
Check the webpage of Schwede.
For Bousfield localization, thick triangulated subcats, and Verdier quotients, see this nLab entry.
For the enriched version of the octahedron axiom (Beilinson, Bernstein, Deligne), see Balmer: Triangular Witt groups. I. The 12-term localization exact sequence (2000)
Balmer and Schlichting: Idempotent completion of triangulated categories.
Beilinson claims on some lecture notes that our notion of triangulated cat is not the right one. Why?
Baues and Muro has a notion of triangulated track category, a 2-dimensional analogue of triangulated categories. In this setting the octahedron axiom holds automatically because of the 2-category structure. See Baues: Triangulated track categories (2006), or ask Muro.
nLab entries
http://ncatlab.org/nlab/show/mapping+cone
http://www.ncatlab.org/nlab/show/triangulated+category
http://www.ncatlab.org/nlab/show/cohomological+functor
Brown representability
There are abstract representability theorems for cohomological functors on triangulated categories. Explain more about this.
Some references
Kuenzer on Heller triangulated cats. See also Schwede's web page, as well as work by Neeman and by Muro.
Neeman book.
J. P. May, The axioms for triangulated categories, preprint.
A. I. Bondal, M. M. Kapranov, Framed triangulated categories, (Russian) Mat. Sb. 181 (1990), no. 5, 669-683
Weight structures, weight filtrations, weight spectral sequences, and weight complexes (for motives and spectra) , by Mikhail V. Bondarko: K0843 or arXiv
Murfet on cocoverings and wellgeneratedness.
Title: Complete intersections and derived categories. Authors: D.J.Benson, J.P.C.Greenlees. We propose a definition of when a triangulated category should be considered a complete intersection. We show (using work of Avramov and Gulliksen) that for the derived category of a complete local Noetherian commutative ring R, the condition on the derived category D(R) holds precisely when R is a complete intersection in the classical sense. http://arxiv.org/abs/0906.4025
http://ncatlab.org/nlab/show/enhanced+triangulated+category
Notes from Kashiwara-Schapira
An additive category with translation is an additive category together with an additive autofunctor. A morphism of such categories is required to commute (up to isomorphism) with the translations. A triangle in an additive category with translation is a sequence
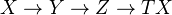 . A morphism of triangles is what you think it is (require last vertical map to be T(first map) ).
. A morphism of triangles is what you think it is (require last vertical map to be T(first map) ).Remark: Sign rule for changing signs in the maps of triangle ("The new triangle is IMic to the old if the signs multiply to one").
A triangulated category is an additive category with translation, together with a family of distinguished triangles satisfying six axioms:
- TR0: "Closed under isomorphism"
- TR1: "X \to X \to 0 \to TX" (first map is id)
- TR2: Every map fits as the first map into some d.t.
- TR3: A triangle X, Y, Z, TX is distinguished iff Y, Z, TX, TY (all maps with a minus sign) is distinguished.
- TR4: A "morphism of triangles but without the third map" can be completed (non-uniquely) to a morphism of triangles.
- TR5: Octahedron axiom
A triangulated functor of triangulated cats is a functor of add cats w transl, sending dt's to dt's.
Prop: In a dt, the map
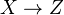 is zero.
is zero.Cohomological functor: A functor from a triangulated category to an abelian category is called cohomological if for any DT (X,Y,Z), the sequence
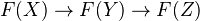 is exact.
is exact.Note that a cohomological functor gives a long exact sequence:
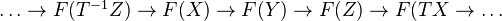
Proposotions: Any Hom functor is cohomological in both variables. In a morphism of DTs, if first two maps are IMs, then so os the third. Criterion for uniqueness in TR4. A triangulated functor is exact. If a tr.category admits direct sums, the direct sum of DTs is a DT. Under some hypotheses, the (Kan???) extension of a cohomological functor to a bigger tr.category is also cohomological.
In a tr.category admitting small direct sums, we can define the notion of a system of t-generators. Morally, this is a family of objects that, regarded as covariant functors, detect when an object is isomorphic to zero, and also has a certain countable direct sum property.
Thm: Let D be a triangulated category with a family F of t-generators. Let
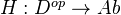 be a cohomological functor which commutes with small products, i.e.
be a cohomological functor which commutes with small products, i.e. 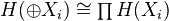 . Then H is representable. Many variants on this thm, for example for cats not admitting small direct sums.
. Then H is representable. Many variants on this thm, for example for cats not admitting small direct sums.Homotopy colimit. In a tr.category, a hocolim of an inductive system
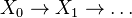 is defined by the DT:
is defined by the DT: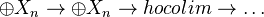
where the first map is
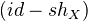
CHAPTER 11: Consider an additive category
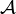 with translation. A differential object is a morphism
with translation. A differential object is a morphism 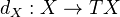 . A complex is a DO such that
. A complex is a DO such that 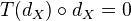 . Have natural notion of morphism of DOs, so get categories
. Have natural notion of morphism of DOs, so get categories 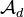 and
and 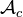 . We define the "shifted object" as
. We define the "shifted object" as 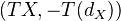 .
Let
.
Let 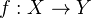 be a morphism in
be a morphism in 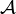 , where
, where 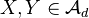 . We define the mapping cone of
. We define the mapping cone of  as
as 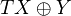 , with differential given by a 2x2 matrix reading
, with differential given by a 2x2 matrix reading 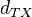 ,
, 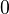 ,
, 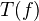 ,
, 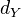 . Prop: MC(f) will be a complex iff
. Prop: MC(f) will be a complex iff  is a morphism of complexes. MC is a functor from
is a morphism of complexes. MC is a functor from 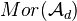 to
to 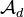 which commutes with functors of add.cats with translation. Define the mapping cone triangle to be
which commutes with functors of add.cats with translation. Define the mapping cone triangle to be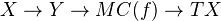
where the second map is
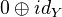 and the third is
and the third is 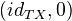 .
.A morphism in
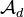 is homotopic to zero if there exists
is homotopic to zero if there exists 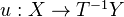 such that
such that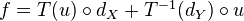
Note: A functor of add.cats w tr. sends zero-homotopic morphisms to zero-homotopic morphisms.
Now define the homotopy category
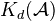 by taking the objects from
by taking the objects from 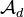 , but modding out the Hom groups by the zero-homotopic morphisms. This is also an additive category. w. tr.
, but modding out the Hom groups by the zero-homotopic morphisms. This is also an additive category. w. tr. Define a DT in the homotopy category to be a triangle IMic to a mapping cone triangle. Thm:
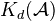 is triangulated. The subcategory
is triangulated. The subcategory 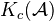 is a triangulated full subcategory. Prop: Any functor (or bifunctor) of add.cats w.tr. induces triangulated functors on
is a triangulated full subcategory. Prop: Any functor (or bifunctor) of add.cats w.tr. induces triangulated functors on 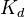 and
and 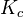 .
. Most interesting examples seem to come from complexes in additive categories. Let
 be additive. Can form the associated graded category by taking
be additive. Can form the associated graded category by taking 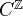 as objects and translation defined by
as objects and translation defined by 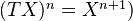 . This is an add.category w.tr. From this we form the category of complexes,
. This is an add.category w.tr. From this we form the category of complexes, 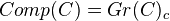 . Notation
. Notation 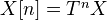 . We have important subcats
. We have important subcats 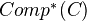 where
where 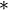 is in
is in 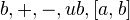 (meaning bounded, bounded below, bounded above, unbounded). These are all additive. Both
(meaning bounded, bounded below, bounded above, unbounded). These are all additive. Both  and
and 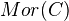 can be viewed as subcats of
can be viewed as subcats of 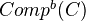 .<]]>
.<]]>- Triangulated category tempWrite comment View comments
http://www.birs.ca/events/2011/5-day-workshops/11w5009
http://mathoverflow.net/questions/1440/freyd-mitchell-for-triangulated-categories
Thomason: The classification of triangulated subcategories. In addition to classification (relating subcats to subgroups of the Grothendieck group) and relation to the Nilpotence theorem, this contains some speculation on the "right" definition of algebraic n-cycles, which should be an object in some triangulated subcategory of the category of perfect complexes. These cycles should give a good notion replacing the Chow ring in cases such as singular algebraic varieties and schemes flat and of finite type over Spec Z. The article also reviews basic notions in triangulated categories, such as thick subcategories, the Grothendieck group, and more.
arXiv:0910.2539 General heart construction on a triangulated category (II): Associated cohomological functor from arXiv Front: math.CT by Noriyuki Abe, Hiroyuki Nakaoka In the preceding part (I) of this paper, we showed that for any torsion pair (i.e., $t$-structure without the shift-closedness) in a triangulated category, there is an associated abelian category, which we call the heart. Two extremal cases of torsion pairs are $t$-structures and cluster tilting subcategories. If the torsion pair comes from a $t$-structure, then its heart is nothing other than the heart of this $t$-structure. In this case, as is well known, by composing certain adjoint functors, we obtain a cohomological functor from the triangulated category to the heart. If the torsion pair comes from a cluster tilting subcategory, then its heart coincides with the quotient category of the triangulated category by this subcategory. In this case, the quotient functor becomes cohomological. In this paper, we unify these two constructions, to obtain a cohomological functor from the triangulated category, to the heart of any torsion pair.
arXiv:1101.3233 Report on locally finite triangulated categories from arXiv Front: math.CT by Henning Krause The basic properties of locally finite triangulated categories are discussed. The focus is on Auslander--Reiten theory and the lattice of thick subcategories.
arXiv:1101.5931 Does full imply faithful? from arXiv Front: math.CT by Alberto Canonaco, Dmitri Orlov, Paolo Stellari We study full exact functors between triangulated categories. With some hypothesis on the source category we prove that it admits an orthogonal decomposition into two pieces such that the functor restricted to one of them is zero while the restriction to the other is faithful. In particular, if the source category is either the category of perfect complexes or the bounded derived category of coherent sheaves on a noetherian scheme supported on a closed connected subscheme, then any non-trivial exact full functor is faithful as well. Finally we show that removing the noetherian hypothesis this result is not true.
arXiv:1102.2879 Stratifying derived categories of cochains on certain spaces from arXiv Front: math.CT by Shoham Shamir In recent years, Benson, Iyengar and Krause have developed a theory of stratification for compactly generated triangulated categories with an action of a graded commutative Noetherian ring. Stratification implies a classification of localizing and thick subcategories in terms of subsets of the prime ideal spectrum of the given ring. In this paper two stratification results are presented: one for the derived category of a commutative ring-spectrum with polynomial homotopy and another for the derived category of cochains on certain spaces. We also give the stratification of cochains on a space a topological content.
<]]>- Tropical algebraic geometryWrite comment View comments
Folder: AG/Tropical
http://mathoverflow.net/questions/83624/why-tropical-geometry
<]]>- Type theoryWrite comment View comments
- <]]>