Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- Van Kampen theoremWrite comment View comments
Goerss-Jardine p 156. A pushout diagram of simplicial sets (with some hyps) induces a pushout diagram of the corresponding fundamental groups.
<]]>- Vandiver conjectureWrite comment View comments
Soulé: Perfect forms and the Vandiver conjecture, in Reine ca 1999. review
<]]>- Vanishing cyclesWrite comment View comments
Superb references: http://mathoverflow.net/questions/56082/vanishing-cycles-in-a-nutshell
http://mathoverflow.net/questions/9492/how-does-one-find-vanishing-algebraic-cycles
Ayoub's work.
arXiv:1002.1686 Notes on Beilinson's "How to glue perverse sheaves" from arXiv Front: math.CT by Ryan Reich The titular, foundational work of Beilinson not only gives a technique for gluing perverse sheaves but also implicitly contains constructions of the nearby and vanishing cycles functors of perverse sheaves. These constructions are completely elementary and show that these functors preserve perversity and respect Verdier duality on perverse sheaves. The work also defines a new, "maximal extension" functor, which is left mysterious aside from its role in the gluing theorem. In these notes, we present the complete details of all of these constructions and theorems.
math/9908107 Notes on Perverse Sheaves and Vanishing Cycles from arXiv Front: math.AG by David B. Massey 1 person liked this A working mathematician's summary of many results on the derived category, perverse sheaves, and vanishing cycles. This is the February 2010 version.
<]]>- VaradarajanWrite comment View comments
Selected works, one vol
<]]>- Varieties examplesWrite comment View comments
Should set up a database for varieties, to absorb examples, and things that are known. For example all the exercises in Hartshorne (at least the first chapter). Other sources: Dieudonne
Brauer-Severi varieties, see Jahnel in AG/Various
Kollar: Rational curves on algebraic varieties. Gives some general introduction to higher-dim varieties I think. In folder AG/Various
Albanese variety
arXiv:1008.3825 Algebraic surfaces and hyperbolic geometry from arXiv Front: math.AG by Burt Totaro This is a survey of the Kawamata-Morrison cone conjecture on the structure of Calabi-Yau varieties and more generally Calabi-Yau pairs. We discuss the proof of the cone conjecture for algebraic surfaces, with plenty of examples.
We show that the automorphism group of a K3 surface need not be commensurable with an arithmetic group, which answers a question by Mazur.arXiv:0908.4241 Lectures on curves on varieties -- Lisbon, 2009 from arXiv Front: math.AG by János Kollár These lectures give a short introduction to the study of curves on algebraic varieties. After an elementary proof of the dimension formula for the space of curves, we summarize the basic properties of uniruled and of rationally connected varieties. At the end, some connections with symplectic geometry are considered.
arXiv:1103.3156 The Expanding Zoo of Calabi-Yau Threefolds from arXiv Front: math.AG by Rhys Davies This is a short review of recent constructions of new Calabi-Yau threefolds with small Hodge numbers and/or non-trivial fundamental group, which are of particular interest for model-building in the context of heterotic string theory. The two main tools are topological transitions and taking quotients by actions of discrete groups. Both of these techniques can produce new manifolds from existing ones, and they have been used to bring many new specimens to the previously sparse corner of the Calabi-Yau zoo where both Hodge numbers are small. Two new manifolds are also obtained here from hyperconifold transitions, including the first example with fundamental group S3, the smallest non-Abelian group.
<]]>- Vector bundlesWrite comment View comments
Maybe books by Huybrechts?
Folder: AG/Vector bundles
Maybe conference program for VBAC09.
Chapter 5 in Ischebeck and Rao, in the Comm alg folder.
http://ncatlab.org/nlab/show/induced+representation explains G-equivariant VBs
http://ncatlab.org/nlab/show/tangent+bundle
VBs on curves: See Vector bundles folder under Geometry.
<]]>- VerdierWrite comment View comments
Demazure, Michel: Jean-Louis Verdier (1935--1989). (French) Gaz. Math. No. 42 (1989), 1. 01A70
<]]>- Verdier dualityWrite comment View comments
For brief intro, see Bernstein and Lunts, first chapter, in Homol alg folder
T Fimmel: Simplicial analogue of Verdier duality. 1994 Russ. Math. Surv. 49 155-156 doi: 10.1070/RM1994v049n02ABEH002219
Iversen big book
http://mathoverflow.net/questions/15560/verdier-duality-via-brown-representability
<]]>- Vertex algebraWrite comment View comments
Related to QFTs. Book by Kac under Algebras (el)
<]]>- Vertex operator algebraWrite comment View comments
- <]]>
- VideosWrite comment View comments
Some Voevodsky videos: http://mathoverflow.net/questions/70602/vladimir-voevodskys-2002-icm-lecture
<]]>- VoevodskyWrite comment View comments
Apparently no personal web page.
For Voevodsky bibliography - see Fields medallists volume.
K-theory archive preprints
Lectures on motivic cohomology 2000/2001 (written by Pierre Deligne)
The Milnor conjecture
Bloch-Kato conjecture for Z/2-coefficients and algebraic Morava K-theories, by Vladimir Voevodsky.
Homology of schemes, II
Letter to Beilinson
Singular homology of abstract algebraic varieties
Homology of schemes, I
Also plenty of the other articles in the arxiv and MathSciNet lists!
List of arXiv preprints, 1 Sep 2008:
- Homotopy theory of simplicial presheaves in completely decomposable topologies. Vladimir Voevodsky. math.AG.
- Unstable motivic homotopy categories in Nisnevich and cdh-topologies. Vladimir Voevodsky. math.AG.
- Lectures on motivic cohomology 2000/2001 (written by Pierre Deligne). Vladimir Voevodsky. math.AG.
- Simplicial radditive functors. Vladimir Voevodsky. math.AG.
- Motivic Eilenberg-Maclane spaces. Vladimir Voevodsky. math.AG.
- Motives over simplicial schemes. Vladimir Voevodsky. math.AG.
- On motivic cohomology with Z/l coefficients. Vladimir Voevodsky. math.AG.
- On the zero slice of the sphere spectrum. Vladimir Voevodsky. math.AG (math.AT (Algebraic topology) (Algebraic topology) (Algebraic topology) (Algebraic topology)).
- Cancellation theorem. Vladimir Voevodsky. math.AG (math.AT (Algebraic topology) (Algebraic topology) (Algebraic topology) (Algebraic topology) math.KT (K-theory) (K-theory) (K-theory) (K-theory)).
- On 2-torsion in motivic cohomology. Vladimir Voevodsky. math.AG.
- Reduced power operations in motivic cohomology. Vladimir Voevodsky. math.AG.
- An exact sequence for Milnor's K-theory with applications to quadratic forms. Dmitry Orlov, Alexander Vishik, Vladimir Voevodsky. math.AG (math.KT (K-theory) (K-theory) (K-theory) (K-theory)).
List of publications based on MathSciNet, 1 Sep 2008:
Dundas, B. I.; Levine, M.; \O stv\ae r, P. A.; Röndigs, O.; Voevodsky, V. Motivic homotopy theory. Lectures from the Summer School held in Nordfjordeid, August 2002. Universitext. Springer-Verlag, Berlin, 2007.
Orlov, D.; Vishik, A.; Voevodsky, V. An exact sequence for $K^M_* / 2$ with applications to quadratic forms. Ann. of Math. (2) 165 (2007), no. 1, 1--13.
Mazza, Carlo; Voevodsky, Vladimir; Weibel, Charles. Lecture notes on motivic cohomology. Clay Mathematics Monographs/AMS.
Voevodsky, V. On the zero slice of the sphere spectrum. Tr. Mat. Inst. Steklova 246 (2004), Algebr. Geom. Metody, Svyazi i Prilozh., 106--115; translation in Proc. Steklov Inst. Math. 2004, no. 3 (246), 93--102
Voevodsky, Vladimir Motivic cohomology with $Z/2$-coefficients. Publ. Math. Inst. Hautes Études Sci. No. 98 (2003), 59--104.
Voevodsky, Vladimir Reduced power operations in motivic cohomology. Publ. Math. Inst. Hautes Études Sci. No. 98 (2003), 1--57.
Voevodsky, Vladimir Open problems in the motivic stable homotopy theory. I. Motives, polylogarithms and Hodge theory, Part I (Irvine, CA, 1998), 3--34, Int. Press.
Voevodsky, Vladimir A possible new approach to the motivic spectral sequence for algebraic $K$-theory. Recent progress in homotopy theory (Baltimore, MD, 2000), 371--379, Contemp. Math., 293, Amer. Math. Soc.
Voevodsky, Vladimir Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic. Int. Math. Res. Not. 2002, no. 7, 351--355.
Voevodsky, Vladimir Triangulated categories of motives over a field. Cycles, transfers, and motivic homology theories, 188--238, Ann. of Math. Stud., 143, Princeton Univ. Press.
Friedlander, Eric M.; Voevodsky, Vladimir Bivariant cycle cohomology. Cycles, transfers, and motivic homology theories, 138--187, Ann. of Math. Stud., 143, Princeton Univ. Press
Voevodsky, Vladimir Cohomological theory of presheaves with transfers. Cycles, transfers, and motivic homology theories, 87--137, Ann. of Math. Stud., 143.
Suslin, Andrei; Voevodsky, Vladimir Relative cycles and Chow sheaves. Cycles, transfers, and motivic homology theories, 10--86, Ann. of Math. Stud., 143, Princeton Univ. Press
Friedlander, Eric M.; Suslin, A.; Voevodsky, V. Introduction. Cycles, transfers, and motivic homology theories, 3--9, Ann. of Math. Stud., 143, Princeton Univ. Press, Princeton, NJ, 2000.
Voevodsky, Vladimir; Suslin, Andrei; Friedlander, Eric M. Cycles, transfers, and motivic homology theories. Annals of Mathematics Studies, 143.
Suslin, Andrei; Voevodsky, Vladimir Bloch-Kato conjecture and motivic cohomology with finite coefficients. The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 117--189, NATO Sci. Ser. C Math. Phys. Sci., 548, Kluwer Acad. Publ., Dordrecht, 2000.
Morel, Fabien; Voevodsky, Vladimir
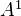 -homotopy theory of schemes. Inst. Hautes Études Sci. Publ. Math. No. 90 (1999), 45--143 (2001).
-homotopy theory of schemes. Inst. Hautes Études Sci. Publ. Math. No. 90 (1999), 45--143 (2001). Voevodsky, V. Voevodsky's Seattle lectures: $K$-theory and motivic cohomology. Notes by C. Weibel. Proc. Sympos. Pure Math., 67, Algebraic $K$-theory (Seattle, WA, 1997), 283--303, Amer. Math. Soc.
Voevodsky, Vladimir $\bold A\sp 1$-homotopy theory. Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998). Doc. Math. 1998, Extra Vol. I, 579--604 (electronic).
Voevodsky, V. Homology of schemes. Selecta Math. (N.S.) 2 (1996), no. 1, 111--153.
Suslin, Andrei; Voevodsky, Vladimir Singular homology of abstract algebraic varieties. Invent. Math. 123 (1996), no. 1, 61--94.
Voevodsky, V. A nilpotence theorem for cycles algebraically equivalent to zero. Internat. Math. Res. Notices 1995, no. 4, 187--198 (electronic).
Kapranov, M. M.; Voevodsky, V. A. $2$-categories and Zamolodchikov tetrahedra equations. Algebraic groups and their generalizations: quantum and infinite-dimensional methods (University Park, PA, 1991), 177--259, Proc. Sympos. Pure Math., 56, Part 2, Amer. Math. Soc.
Kapranov, M.; Voevodsky, V. Braided monoidal $2$-categories and Manin-Schechtman higher braid groups. J. Pure Appl. Algebra 92 (1994), no. 3, 241--267.
Voevodskiĭ, V. A. Galois groups of function fields over fields of finite type over $Q$. (Russian) Uspekhi Mat. Nauk 46 (1991), no. 5(281), 163--164; translation in Russian Math. Surveys 46 (1991), no. 5, 202--203.
Voevodskiĭ, V. A. Galois representations connected with hyperbolic curves. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 55 (1991), no. 6, 1331--1342; translation in Math. USSR-Izv. 39 (1992), no. 3, 1281--1291.
Kapranov, M. M.; Voevodsky, V. A. $\infty$-groupoids and homotopy types. International Category Theory Meeting (Bangor, 1989 and Cambridge, 1990). Cahiers Topologie Géom. Différentielle Catég. 32 (1991), no. 1, 29--46.
Kapranov, M. M.; Voevodsky, V. A. Combinatorial-geometric aspects of polycategory theory: pasting schemes and higher Bruhat orders (list of results). International Category Theory Meeting (Bangor, 1989 and Cambridge, 1990). Cahiers Topologie Géom. Différentielle Catég. 32 (1991), no. 1, 11--27.
Voevodskiĭ, V. A.; Kapranov, M. M. The free $n$-category generated by a cube, oriented matroids and higher Bruhat orders. (Russian) Funktsional. Anal. i Prilozhen. 25 (1991), no. 1, 62--65; translation in Funct. Anal. Appl. 25 (1991), no. 1, 50--52
Shabat, G. B.; Voevodsky, V. A. Drawing curves over number fields. The Grothendieck Festschrift, Vol. III, 199--227, Progr. Math., 88, Birkhäuser Boston, Boston, MA, 1990.
Voevodskiĭ, V. A. Étale topologies of schemes over fields of finite type over $Q$. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 54 (1990), no. 6, 1155--1167; translation in Math. USSR-Izv. 37 (1991), no. 3, 511--523
Voevodskiĭ, V. A.; Kapranov, M. M. $\infty$-groupoids as a model for a homotopy category. (Russian) Uspekhi Mat. Nauk 45 (1990), no. 5(275), 183--184; translation in Russian Math. Surveys 45 (1990), no. 5, 239--240
Voevodskiĭ, V. A.; Shabat, G. B. Equilateral triangulations of Riemann surfaces, and curves over algebraic number fields. (Russian) Dokl. Akad. Nauk SSSR 304 (1989), no. 2, 265--268; translation in Soviet Math. Dokl. 39 (1989), no. 1, 38--41
Selected publications/preprints:
- Homology of schemes (1996)
- The orange book
- On 2-torsion in motivic cohomology. Preprint 2001
- Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic (2002)
- On motivic cohomology with
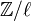 coefficients. Preprint 2003
coefficients. Preprint 2003 - Lectures on cross functors
<]]>