Glossary
Letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Other
- WaldhausenWrite comment View comments
Waldhausen: Algebraic K-theory of spaces. LNM 1126 (1985)
nLab: Waldhausen category
<]]>- Waldhausen S-constructionWrite comment View comments
- <]]>
- Wall crossingWrite comment View comments
- <]]>
- Weak equivalenceWrite comment View comments
- <]]>
- Weak generatorWrite comment View comments
In a (pre-)triangulated category, a set of weak generators is a set of objects
 such that
such that 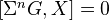 for all
for all  and
and  implies
implies 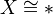 .<]]>
.<]]>- Weak homotopy equivalenceWrite comment View comments
- <]]>
- Weak limitWrite comment View comments
- <]]>
- WeibelWrite comment View comments
- <]]>
- WeightWrite comment View comments
arXiv:1003.0927 Weights in arithmetic geometry from arXiv Front: math.AG by Uwe Jannsen The concept of weights on the cohomology of algebraic varieties was initiated by fundamental ideas and work of A. Grothendieck and P. Deligne. It is deeply connected with the concept of motives and appeared first on the singular cohomology as the weights of (possibly mixed) Hodge structures and on the etale cohomology as the weights of eigenvalues of Frobenius. But weights also appear on algebraic fundamental groups and in p-adic Hodge theory, where they become only visible after applying the comparison functors of Fontaine. After rehearsing various versions of weights, we explain some more recent applications of weights, e.g., to Hasse principles and the computation of motivic cohomology, and discuss some open questions.
Warning: I think that modular weight is different (perhaps plus/minus one) from geometric/motivic weight.
See David Hebert, on arxiv and maybe elsewhere, for weight structures on Beilinson motives. See also work of Bondarko.
Check Deligne ICM1974 talk!
What is the weight spectral sequence? And what does "for weight reasons" mean, in spectral sequence arguments and elsewhere?
Andrzej Weber: Topological properties of the weight filtration (talk). Related to homology of complex algebraic varieties, and to intersection homology. Main point, I think:
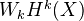 and
and 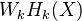 are topological invariants.
are topological invariants.arXiv:1002.2651 Z[1/p]-motivic resolution of singularities from arXiv Front: math.KT by Mikhail V. Bondarko The main goal of this paper is to deduce (from a recent resolution of singularities result of Gabber) the following fact: (effective) Chow motives with $Z[1/p]$-coefficients over a perfect field $k$ of characteristic $p$ generate the category $DM^{eff}{gm}[1/p]$ (of effective geometric Voevodsky's motives with $Z[1/p]$-coefficients). It follows that $DM^{eff}{gm}[1/p]$ could be endowed with a Chow weight structure $w{Chow}$ whose heart is $Chow^{eff}[1/p]$ (weight structures were introduced in a preceding paper, where the existence of $w{Chow}$ for $DM^{eff}{gm}Q$ was also proved). As shown in previous papers, this statement immediately yields the existence of a conservative weight complex functor $DM^{eff}{gm}[1/p]\to K^b(Chow^{eff}[1/p])$ (which induces an isomorphism on $K0$-groups), as well as the existence of canonical and functorial (Chow)-weight spectral sequences and weight filtrations for any cohomology theory on $DM^{eff}{gm}[1/p]$. We also define a certain Chow t-structure for $DM_{-}^{eff}[1/p]$ and relate it with unramified cohomology. To this end we study birational motives and birational homotopy invariant sheaves with transfers.
arXiv:1102.4370 Weights on cohomology and invariants of singularities from arXiv Front: math.AG by Donu Arapura, Parsa Bakhtary, Jarosław Włodarczyk In this paper, we extract natural invariants of a singularity by using the Deligne weight filtration on the cohomology of an exceptional fibre of a resolution, and also on the intersection cohomology of the link. Our primary goal is to study and give natural bounds on the weights in terms of direct images of differential forms. These bounds can be made explicit for various standard classes such as rational, isolated normal Cohen-Macaulay and toroidal singularities, and lead to strong restrictions on the topology of these singularities. A secondary goal of this paper is to make the weight filtration, and related constructions, more widely accessible. So we have tried to make the presentation somewhat self contained. This is supersedes our earlier preprint arXiv:0902.4234.
<]]>- Weight filtrationWrite comment View comments
http://mathoverflow.net/questions/117432/splitting-of-the-weight-filtration (there are also other MO questions on the weight filtration)
In the letter to Beilinson, Voevodsky formulates axioms for a homology theory. He considers
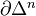 as an (n-1)-dim sphere, write also S for the 1-dim sphere in this sense. Let Sch/k be the cat of separated schemes of finite type over a base k. Then a homological theory is a functor from Sch/k together with a family of natural isos
as an (n-1)-dim sphere, write also S for the 1-dim sphere in this sense. Let Sch/k be the cat of separated schemes of finite type over a base k. Then a homological theory is a functor from Sch/k together with a family of natural isos 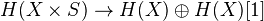 . This functor should satisfy some conditions: Morally, homotopy invariance, MV exact triangle, an exact triangle for blowups, and transfer for flat finite morphisms. Get a 2-cat of homological theories over
. This functor should satisfy some conditions: Morally, homotopy invariance, MV exact triangle, an exact triangle for blowups, and transfer for flat finite morphisms. Get a 2-cat of homological theories over  . Examples: Algebraic K-th with rational coeffs, l-adic homology, Hodge homology ass to a complex embedding. Thm: There is an initial object
. Examples: Algebraic K-th with rational coeffs, l-adic homology, Hodge homology ass to a complex embedding. Thm: There is an initial object 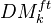 in this cat, which we call the triang cat of eff mixed motives over k. Notion of reduced homological theory, and reduced motive of a scheme. Any motive in the above sense is of the form
in this cat, which we call the triang cat of eff mixed motives over k. Notion of reduced homological theory, and reduced motive of a scheme. Any motive in the above sense is of the form 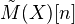 , where we may assume
, where we may assume  affine and
affine and 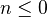 . Tate object and comparison with K-theory. Bigger cat
. Tate object and comparison with K-theory. Bigger cat 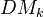 which contains the previous as a full triang subcat, but admits a more explicit description rather than just the universal property. Can also be viewed as the closure of the previous, wrt direct sums and inductive limits. Need the h-topology, in particular coverings including surjective blowups, finite surjetive maps, etale coverings. Various filtrations on
which contains the previous as a full triang subcat, but admits a more explicit description rather than just the universal property. Can also be viewed as the closure of the previous, wrt direct sums and inductive limits. Need the h-topology, in particular coverings including surjective blowups, finite surjetive maps, etale coverings. Various filtrations on 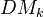 (homotopy canonical, geometrical, motivic canonical, weight). The weight filtr should be related to pure numerical motives.<]]>
(homotopy canonical, geometrical, motivic canonical, weight). The weight filtr should be related to pure numerical motives.<]]>- Weighted limitWrite comment View comments
nLab, see also weighted colimit
Alex Shannon gave a talk at some point about something related I think.
<]]>- WeilWrite comment View comments
Collected papers, several volumes
<]]>- Weil conjecturesWrite comment View comments
See Freitag-Kiehl, original articles of Dwork and Deligne, and lots of printed stuff in my office.
Kiehl and Weissauer: Weil conj, perverse sheaves, etc
Katz and Messing: Some consequences of the Riemann hypothesis for varieties over finite fields (1974)
Mazur: Extremely readable survey
SBS concluding post: http://sbseminar.wordpress.com/2010/06/10/motive-ating-the-weil-conjecture-proof/
http://sbseminar.wordpress.com/2010/04/12/the-weil-conjectures-and-the-problem-of-coefficients/
http://sbseminar.wordpress.com/2010/04/19/the-weil-conjectures-curves/
Some early writings:
- Chevalley, Bourbaki exp 3 and 9, for curves
- Exp 39, Delsarte
- Bourbaki exp 66 (Neron): Arithmetic on algebraic varieties
Irene had a book with some background.
The MathSciNet review of Deligne: La conjecture de Weil I, is very long and informative, with good historical references
<]]>- Weil pairingWrite comment View comments
- <]]>
- Weil-style algebraic geometryWrite comment View comments
- <]]>
- WeylWrite comment View comments
Gesammelte Abhandlungen, 4 vols
<]]>- WhiteheadWrite comment View comments
Mathematical works, 4 vols
<]]>- Whitehead theoremWrite comment View comments
For two fibrant simplicial sets
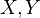 , if a map
, if a map 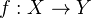 is a weak equivalence, then it is a homotopy equivalence.<]]>
is a weak equivalence, then it is a homotopy equivalence.<]]>- Whitehead towerWrite comment View comments
- <]]>
- WittWrite comment View comments
Collected papers, one vol?
<]]>- Witt vectorsWrite comment View comments
http://mathoverflow.net/questions/512/what-is-interesting-useful-about-big-witt-vectors
http://mathoverflow.net/questions/58/is-there-a-universal-property-for-witt-vectors
http://www.neverendingbooks.org/index.php/big-witt-vectors-for-everyone-12.html
http://www.noncommutative.org/index.php/cartiers-big-witt-functor.html
What are Witt vectors: http://chromotopy.org/?p=444
<]]>